1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Под оценками показателей надежности понимают точечную или интервальную (границы доверительного интервала, который с заданной вероятностью содержит истинное значение показателя) оценки показателя.
1.2. Оценки показателей надежности используют при количественном анализе надежности и (или) при контроле показателей надежности с помощью доверительных границ по ГОСТ 27.410.
1.3. Для вычисления оценок показателей надежности проводят следующие работы:
1) выбор плана испытаний на надежность;
2) планирование испытаний;
3) сбор необходимой информации;
4) статистическую обработку информации.
В технически обоснованных случаях допускается не проводить планирование испытаний.
1.4. Обозначения, применяемые в методических указаниях, приведены в приложении 1.
1.5. Термины, применяемые в методических указаниях, и пояснения к ним приведены в приложении 2.
2. ВЫБОР ПЛАНА ИСПЫТАНИЙ НА НАДЕЖНОСТЬ
2.1. План испытаний на надежность устанавливает число объектов испытаний, порядок проведения испытаний (с восстановлением работоспособного состояния изделия после отказа, заменой отказавшего изделия или без восстановления и замены) и критерий их прекращения.
2.2. Обозначения и определения планов испытаний на надежность - по ГОСТ 27.410.
2.3. Объектами испытаний являются однотипные изделия, не имеющие конструктивных или других различий, изготовленные по единой технологии и испытываемые в идентичных условиях.
2.4. Выбор планов испытаний зависит от типа объекта испытаний, целей испытаний, оцениваемых показателей надежности, условий испытаний и других технико-экономических факторов.
2.5. Рекомендации по выбору планов испытаний приведены в приложении 3.
3. ПЛАНИРОВАНИЕ ИСПЫТАНИЙ НА НАДЕЖНОСТЬ
3.1. Планирование испытаний на надежность предусматривает определение требуемого объема испытаний для вычисления оценок показателей надежности с заданной точностью (относительной ошибкой 
в оценке показателя надежности) и достоверностью (доверительной вероятностью 
).
3.2. Под объемом испытаний понимают для планов:
- число объектов испытаний 
или число восстановлений работоспособного состояния (при испытаниях для оценки показателя среднее время восстановления);
, 
, 
- число объектов и число отказов (предельных состояний) 
испытываемых объектов;
, 
, 
- число объектов испытаний и продолжительность испытаний 
.
3.3. Исходными данными для расчета объема испытаний служат:
доверительная вероятность интервальной оценки соответствующего показателя надежности;
предельная относительная ошибка оценки соответствующего показателя надежности:
;
коэффициент вариации 
распределения случайной величины (наработки, ресурса, срока службы, времени восстановления, срока сохраняемости);
вид закона распределения случайной величины (наработки, ресурса, срока службы, времени восстановления, срока сохраняемости);
объем совокупности 
(для совокупности ограниченного объема).
В технически обоснованных случаях допускается вместо предельной относительной ошибки использовать относительную ошибку оценки соответствующего показателя надежности:
3.4. Доверительную вероятность рекомендуется выбирать из ряда: 0,80; 0,90; 0,95; 0,99.
Предельную относительную ошибку (относительную ошибку) рекомендуется выбирать из ряда: 0,05; 0,10; 0,15; 0,20.
Значения и для планирования испытаний устанавливают в программе испытаний на надежность по ГОСТ 27.410 или программах наблюдений по РД 50-204.
3.5. Рекомендации по выбору значений и приведены в приложении 3.
3.6. Порядок расчета объема испытаний приведен в приложении 4.
4. ИСХОДНАЯ ИНФОРМАЦИЯ ДЛЯ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
4.1. Исходную информацию для оценки показателей надежности (исходная информация) подразделяют на два вида:
экспериментальная - о наработках работоспособных и неработоспособных объектов или их составных частей;
информация о структуре объекта, взаимодействии составных частей, принятых способах резервирования, которую представляют в виде структурной схемы надежности.
4.2. Экспериментальную информацию подразделяют на два вида:
основная - полученная в результате испытаний или эксплуатации исследуемого объекта или его составных частей;
дополнительная - полученная в результате испытаний или эксплуатации объектов-аналогов (или аналогов его составных частей), объектов-прототипов и объектов-аналогов, имеющих отличный от исследуемого режим испытаний или эксплуатации.
4.3. Экспериментальная информация зависит от плана испытаний. Исходными данными для оценки показателей надежности служат:
4.3.1. При плане
выборочные значения наработки до отказа, ресурса, срока службы, времени восстановления, срока сохраняемости 
, 
, ..., 
;
объем выборки .
4.3.2. При плане
выборочные значения наработки до отказа, ресурса, срока службы, срока сохраняемости , ,..., 
;
число отказов ;
объем выборки .
4.3.3. При плане
выборочные значения наработки до отказа, ресурса, срока службы, срока сохраняемости , , ..., 
;
продолжительность испытаний ;
объем выборки .
4.3.4. При плане 
выборочные значения наработки до отказа, ресурса, срока службы, срока сохраняемости , , ..., ;
выборочные значения наработки работоспособных изделий (наработки до цензурирования) 
, 
, …, 
;
число отказов ;
объем выборки .
4.3.5. При планах ,
выборочные значения наработки между отказами , , …, ;
число отказов ;
объем выборки .
4.3.6. При планах ,
выборочные значения наработки между отказами , , …, ;
продолжительность испытаний ;
объем выборки .
5. МЕТОДЫ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
5.1. Оценка показателей надежности при наличии основной экспериментальной информации (экспериментальный метод).
5.1.1. Показатели надежности оценивают двумя методами:
непараметрическим - при неизвестном законе распределения, включающим непосредственную оценку показателей надежности;
параметрическим - при известном законе распределения, включающим оценку параметров закона распределения, входящих в расчетную формулу оцениваемого показателя надежности, и оценку показателя надежности по вычисленным оценкам параметров закона распределения.
5.1.2. Параметрические методы оценки показателей надежности, установленные в настоящем стандарте, применяют для экспоненциального, нормального, логарифмически нормального и диффузионных распределений и распределения Вейбулла.
5.1.3. Проверку согласия опытного закона распределения с теоретическим для случая испытаний по плану проводят до СТ СЭВ 1190.
5.1.4. Порядок оценки показателей надежности приведен в приложении 5.
5.1.5. Если надежность изделий характеризуется показателем вероятности безотказной работы, а условия испытания (эксплуатации) изделий не позволяют определить моменты возникновения их отказов, то оценку вероятности безотказной работы вычисляют по формулам приложения 8 (случай биномиального распределения).
5.2. Оценка показателей надежности при наличии основной экспериментальной информации о составных частях объекта и информации о его структуре (расчетно-экспериментальный метод).
5.2.1. Вычисляют точечные оценки показателей надежности объекта.
Для этого на основе структурной схемы надежности (ССН) составляют функцию связи показателя надежности объекта с показателями надежности составных частей:
,
где 
- показатель надежности 
-й составной части;
- число составных частей, входящих в ССН.
Функцию связи 
составляют в соответствии с РД 50-476.
По основной экспериментальной информации о составных частях объекта в соответствии с приложением 5 вычисляют точечные оценки показателей надежности составных частей.
Точечную оценку показателя надежности 
объекта вычисляют подстановкой оценок 
в функцию связи:
.
5.2.2. Интервальные оценки показателей надежности вычисляют в соответствии с РД 50-476.
5.3. Оценка показателей надежности при наличии основной и дополнительной информации об объекте (расчетно-экспериментальный метод).
5.3.1. Оценку показателей надежности вычисляют двумя методами:
параметрическим - при известных видах законов распределения наработки изделия и изделия-аналога в предположении, что вид закона распределения изделия и аналога одинаков;
непараметрическим - при неизвестных видах закона распределения наработки изделия и изделия-аналога.
5.3.2. Параметрические методы оценки показателей надежности применяют для экспоненциального, нормального, логарифмически нормального распределений и распределения Вейбулла в типовых ситуациях, представленных в табл.1.
Таблица 1
|
Обозначение типовых ситуаций (ТС) |
Краткое описание ТС |
Информация относительно |
|
ТС-1 |
Однотипные изделия находятся в одинаковых условиях и показатели надежности этих элементов одинаковы |
|
|
ТС-2 |
Однотипные изделия находятся в различных условиях. Известны отношения параметров законов распределения элементов |
Известно |
|
ТС-3 |
Однотипные изделия находятся в различных условиях. Известны диапазоны изменения отношения параметров в зависимости от нахождения в тех или иных условиях |
Известны диапазоны изменения
|
|
ТС-4 |
Однотипные изделия находятся в различных условиях. Заведомо известно, что показатели в одних условиях больше, чем в других |
Известно, что |
Формальным признаком, по которому классифицируют типовые ситуации, является информация относительно коэффициентов 
, характеризующих отношение параметров распределений, описывающих дополнительную и основную информацию. Для рассмотренных законов распределения эти отношения приведены в табл.2.
Здесь 
- количество групп объектов-аналогов.
Таблица 2
Значения коэффициента 
|
Закон распределения |
Плотность вероятности распределения |
Известный параметр |
Отношения параметров распределений |
|
Экспоненциальный |
|
- |
|
|
Нормальный |
|
|
|
|
Логарифмически нормальный |
|
|
|
|
Вейбулла |
|
|
|
Примечание. Индекс "1" относится к параметрам распределения наработки оцениваемого объекта.
5.3.3. Непараметрический метод оценки показателей надежности применяют в предположении:
виды законов распределения наработки изделия и изделия-аналога неизвестны;
оцениваемое изделие и изделия-аналоги находятся в одинаковых условиях;
номенклатура показателей надежности оцениваемого изделия и изделий-аналогов совпадают.
5.3.4. Порядок вычисления оценок показателей надежности приведен в приложении 6.
5.4. Оценка показателей надежности при наличии основной и дополнительной информации о составных частях объекта и о его структуре (расчетно-экспериментальный метод).
5.4.1. Оценки показателей надежности объекта вычисляют в два этапа:
определяют точечные и интервальные оценки показателей надежности составных частей объекта;
определяют точечные и интервальные оценки показателей надежности объекта в целом.
5.4.2. Точечные и интервальные оценки показателей надежности составных частей объекта определяют в соответствии с приложением 6.
5.4.3. Точечные оценки показателей надежности объекта в целом определяют по формуле:
,
где 
- точечные оценки показателей надежности составных частей;
- функция связи показателя надежности объекта в целом с показателями надежности составных частей;
- количество составных частей.
5.4.4. Интервальные оценки показателей надежности объекта определяют в зависимости от структурной схемы надежности объекта методом подстановки в соответствии с РД 50-476.
5.5. Оценка показателей надежности, вычисленная в соответствии с пп.5.2-5.4, не используется для контроля показателей надежности.
5.6. Метод последовательных приближений для оценки параметров распределения (случай основной экспериментальной информации) приведен в приложении 7.
5.7. Таблицы для оценки показателей надежности приведены в приложении 9.
5.8. Примеры планирования испытаний и оценки показателей надежности приведены в приложении 10.
ПРИЛОЖЕНИЕ 1
Справочное
ОБОЗНАЧЕНИЯ, ПРИМЕНЯЕМЫЕ В МЕТОДИЧЕСКИХ УКАЗАНИЯХ
- оценка показателя надежности 
;
- предельная относительная ошибка (относительная ошибка) оценки показателя надежности ;
- нижняя доверительная граница показателя надежности ;
- верхняя доверительная граница показателя надежности ;
- число испытываемых (наблюдаемых) изделий;
- объем совокупности;
- доверительная вероятность, соответствующая одностороннему доверительному интервалу;
* - доверительная вероятность, соответствующая двустороннему доверительному интервалу;
- число отказов (предельных состояний) за время испытаний (наблюдений);
- отдельные значения случайной величины (наработки до отказа, наработки между отказами, ресурса, срока службы, срока сохраняемости);
- отдельные значения времени восстановления;
- отдельные значения наработки до цензурирования;
- оценка параметра 
экспоненциального распределения;
- оценки параметров 
, 
распределения Вейбулла;
, 
- оценки параметров 
, 
нормального распределения;
- оценка функции распределения 
для наработки 
(вероятность отказа за наработку );
- оценка вероятности безотказной работы 
за наработку ;
- оценка средних показаний надежности 
;
, 
- оценки параметров диффузионных распределений;
- оценка гамма-процентных показателей надежности 
;
- суммарная наработка изделий за время испытаний;
- квантиль нормального распределения, соответствующая вероятности ;
- квантиль ХИ-квадрат распределения с числом степеней свободы , соответствующая вероятности ;
- квантиль -распределения (Стьюдента) с числом степеней свободы , соответствующая вероятности ;
- регламентированная вероятность;
- оценка коэффициента вариации ;
- функция нормального распределения (нормированного);
- плотность вероятности нормального распределения;
- гамма-функция;
- коэффициент, учитывающий поправку на смещение при оценке параметра ;
- относительная продолжительность испытаний;
- коэффициент вариации времени восстановления;
- продолжительность испытаний;
- оценка среднего квадратического отклонения наработки между отказами;
- оценка среднего квадратического отклонения времени восстановления;
- коэффициент, учитываемый при оценке гамма-процентной наработки до отказа для нормального распределения;
- коэффициент, учитываемый при оценке нижней доверительной границы вероятности безотказной работы при биномиальных испытаниях;
- обратное отношение Миллса;
- поправочный коэффициент.
ПРИЛОЖЕНИЕ 2
Справочное
ПРИМЕНЯЕМЫЕ ТЕРМИНЫ И ПОЯСНЕНИЯ К НИМ
Таблица 3
|
Термин |
Пояснение |
|
1. Цензурирование справа |
Событие, приводящее к прекращению испытаний или эксплуатационных наблюдений объекта до наступления отказа (предельного состояния) изучаемого характера. |
|
|
Примечание. Причинами цензурирования являются: |
|
|
разновременность начала и (или) окончания испытаний или эксплуатации изделий; |
|
|
снятие с испытаний или эксплуатации некоторых изделий по организационным причинам или из-за отказов составных частей, надежность которых не исследуется; |
|
|
перевод изделий из одного режима применения в другой в процессе испытаний или эксплуатации; |
|
|
необходимость оценки надежности до наступления отказов всех испытываемых изделий |
|
2. Наработка до цензурирования |
Наработка объекта от начала испытаний или эксплуатационных наблюдений до наступления цензурирования |
|
3. Цензурированная выборка |
Выборка, элементами которой являются значения наработки до отказа и наработки до цензурирования |
|
4. Однократно цензурированная выборка |
Цензурированная выборка, в которой значения всех наработок до цензурирования равны между собой и не меньше наибольшей наработки до отказа |
|
5. Многократно цензурированная выборка |
Цензурированная выборка, в которой значения наработок до цензурирования не равны между собой |
|
6. Позитивный показатель надежности |
Показатель надежности, значение которого увеличивается при повышении надежности объекта. |
|
|
К позитивным показателям относятся, например, средняя наработка до отказа, гамма-процентный ресурс и т.д. |
|
7. Негативный показатель надежности |
Показатель надежности, значение которого уменьшается при повышении надежности. |
|
|
К негативным показателям относятся, например, интенсивность отказов, среднее время восстановления и т.д. |
|
8. Объем совокупности |
Число единиц продукции (объектов), составляющих генеральную совокупность |
ПРИЛОЖЕНИЕ 3
Рекомендуемое
РЕКОМЕНДАЦИИ ПО ВЫБОРУ ПЛАНОВ ИСПЫТАНИЙ И ИСХОДНЫХ ДАННЫХ
ДЛЯ ПЛАНИРОВАНИЯ
1. Рекомендации по выбору планов определительных испытаний на надежность приведены в табл.4.
Таблица 4
Рекомендуемые планы определительных испытаний на надежность
|
Вид объекта |
Показатель надежности |
План испытаний |
Примечание |
|
Невосста- |
Средняя наработка до отказа |
|
Для сокращения продолжительности испытаний применяют планы |
|
|
Гамма-процентная наработка до отказа |
|
|
|
|
Интенсивность отказов |
|
Для повышения точности оценок показателей - |
|
|
Вероятность безотказной работы |
|
|
|
Восстанав- |
Средняя наработка на отказ |
|
|
|
|
Средний ресурс |
|
Рассматривают применительно к предельным состояниям. |
|
|
Гамма-процентный ресурс |
|
Для сокращения продолжительности испытаний применяют планы |
|
|
|
|
Для повышения точности оценок показателей - |
|
|
Среднее время восстановления |
|
Рассматривают применительно к восстановлению работоспособного состояния и переходят к плану |
|
|
Коэффициент готовности |
|
|
|
Произвольного вида |
Средний срок сохраняемости |
|
|
|
|
Гамма-процентный срок сохраняемости |
|
|
,
2. Значения относительной ошибки и доверительной вероятности устанавливают с учетом следующих факторов:
2.1. Для контроля показателей надежности по одному уровню с помощью доверительных границ
- при контроле позитивных показателей надежности;
- при контроле негативных показателей надежности;
,
где 
- риск потребителя.
В остальных случаях задают предельную относительную ошибку.
2.2. Для составных частей изделия, влияющих на безопасность, =0,05; =0,95; 0,99;
для базовых составных частей изделия =0,10; 0,15; =0,90, 0,95;
для деталей, обусловливающих внешний вид изделия, его комфортабельность, =0,15; 0,20; =0,80; 0,90;
для изделий массового и серийного производств =0,10; =0,90.
2.3. Для изделий крупногабаритных, дорогих, мелкосерийного производства значения допускается увеличивать, значения - уменьшать.
ПРИЛОЖЕНИЕ 4
Рекомендуемое
ПОРЯДОК РАСЧЕТА ОБЪЕМА ИСПЫТАНИЙ
1. Определение объема испытаний для плана .
1.1. Объем испытаний для оценки средней наработки до отказа, среднего ресурса (срока службы, времени восстановления) определяют по табл.5-9 для совокупностей неограниченного объема и по табл.10-19 для совокупностей ограниченного объема.
Исходные данные для расчета:
предельная относительная ошибка ;
доверительная вероятность ;
вид закона распределения случайной величины (наработки до отказа, ресурса, срока службы, времени восстановления);
коэффициент вариации ;
объем совокупности (для совокупностей ограниченного объема).
1.2. Объем испытаний для оценки гамма-процентной наработки до отказа, гамма-процентного ресурса (срока службы) определяют по табл.20-25.
Исходные данные для расчета:
предельная относительная ошибка ;
доверительная вероятность ;
регламентированная вероятность ;
вид закона распределения случайной величины;
предполагаемый коэффициент вариации .
1.3. Если по результатам испытаний получен коэффициент вариации больше заданного, то объем испытаний пересчитывают для найденного коэффициента вариации (пп.1.1-1.2) и испытания продолжают.
2. Определение объема испытаний для плана
2.1. Число отказов (предельных состояний) для оценки средней наработки до отказа, среднего ресурса (срока службы, срока сохраняемости) определяют по табл.5-9, полагая вместо значение для совокупностей неограниченного объема.
Исходные данные для расчета - по п.1.1.
2.2. Объем выборки определяют в предположении, что задана относительная продолжительность испытаний 
:
для нормального распределения:
,
где {
} - целая часть :
для распределения Вейбулла (экспоненциального):
;
для логарифмически нормального распределения:
;
для диффузионного монотонного распределения:
,
для диффузионного немонотонного распределения:
.
2.3. Число отказов (предельных состояний) для оценки гамма-процентной наработки до отказа, гамма-процентного ресурса (срока службы, срока сохраняемости) определяют приближенно по табл.20-25, полагая вместо значение .
Исходные данные для расчета - по п.1.2.
2.4. Объем выборки определяют по п.2.2 в предположении, что задана относительная продолжительность испытаний .
2.5. Если по результатам испытаний получен коэффициент вариации больше заданного, то объем испытаний пересчитывают для найденного коэффициента вариации (пп.2 1-2.4) и испытания продолжают.
2.6. Объем выборки для оценки гамма-процентной наработки до отказа, гамма-процентного ресурса (срока службы, срока сохраняемости), вероятности безотказной работы при неизвестном законе распределения определяют по табл.26.
Исходные данные для расчета:
доверительная вероятность ;
регламентированная вероятность или предполагаемое значение ;
установленное число отказов (предельных состояний) .
Число отказов (предельных состояний) для оценки гамма-процентных показателей надежности или вероятности безотказной работы определяют по табл.26 в предположении, что число испытываемых объектов задано.
3. Определение объема испытаний для плана
3.1. Объем выборки или относительную продолжительность испытаний для оценки средней наработки до отказа, среднего ресурса (срока службы, срока сохраняемости) определяют в следующей последовательности:
для исходных данных по п.1.1 определяют прогнозируемое число отказов (предельных состояний) по табл.5-9, полагая вместо значения ;
для найденного значения определяют объем выборки по формулам п.2.2, полагая, что относительная продолжительность испытаний задана, или определяют значение , полагая, что объем выборки задан.
3.2. Объем выборки или относительную продолжительность испытаний для оценки гамма-процентной наработки до отказа, гамма-процентного ресурса (срока службы, срока сохраняемости) определяют приближенно в следующей последовательности:
для исходных данных по п.2.1 определяют прогнозируемое число отказов (предельных состояний) по табл.20-25, полагая вместо значения ;
для найденного значения определяют объем выборки по формулам п.2.2, полагая, что относительная продолжительность испытаний задана, или определяют значение , полагая, что объем выборки задан.
3.3. Объем выборки для оценки гамма-процентной наработки до отказа, гамма-процентного ресурса (срока службы, срока сохраняемости), вероятности безотказной работы при неизвестном виде закона распределения определяют по табл.26, предполагая известным значение для исходных данных по п.2.6.
3.4. Если по результатам испытаний за объектами за время получено число отказов (предельных состояний) меньше прогнозируемого, то испытания следует продолжить до наступления отказов (предельных состояний) или снизить требования к точности и (или) достоверности оценки показателя.
3.5. Объем выборки при испытаниях по плану без фиксации наработки до отказа (биномиальные испытания) при оценке вероятности безотказной работы за наработку определяют по табл.28.
Исходные данные для расчета:
нижняя доверительная граница вероятности безотказной работы 
за наработку (ожидаемое значение);
доверительная вероятность ;
допустимое число отказов 
.
При известном значении по табл.28 находят допустимое число отказов .
4. Определение объема испытаний для планов , , , .
4.1. Для планов , число отказов для оценки средней наработки на отказ (до отказа) определяют по табл.27 в предположении экспоненциального закона распределения наработки между отказами (до отказа).
Исходные данные для расчета:
предельная относительная ошибка ;
доверительная вероятность .
4.2. Для плана и неизвестного закона распределения наработки между отказами число отказов для оценки коэффициента готовности 
определяют по табл.29-35.
Исходные данные для расчета:
предельная относительная ошибка ;
доверительная вероятность ;
предполагаемый коэффициент вариации распределения наработки между отказами;
предполагаемый коэффициент вариации распределения времени восстановления.
Если по результатам испытаний получен коэффициент вариации (при больше заданного), то число отказов пересчитывают по табл.29-35 для найденного коэффициента вариации и испытания продолжают.
4.3. Для планов и объем выборки или относительную продолжительность испытаний для оценки средней наработки на отказ (до отказа) вычисляют по формуле
.
Прогнозируемое число отказов определяют по п.4.1.
5. Если вид закона распределения случайной величины неизвестен (кроме пп.2.6, 3.3, 3.5, 4.1-4.3), то для имеющихся исходных данных объем испытаний принимают равным максимальным значениям.
Таблица 5
Число объектов испытаний при плане и нормальном распределении
|
|
|
|
| ||||
|
|
|
|
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
|
0,05 |
- |
0,80 |
4 |
8 |
12 |
19 |
26 |
|
|
0,80 |
0,90 |
8 |
16 |
28 |
40 |
65 |
|
|
0,90 |
0,95 |
13 |
26 |
45 |
65 |
100 |
|
|
0,95 |
0,975 |
18 |
37 |
65 |
100 |
150 |
|
|
0,98 |
0,99 |
25 |
52 |
90 |
140 |
200 |
|
0,10 |
- |
0,80 |
2 |
3 |
4 |
6 |
8 |
|
|
0,80 |
0,90 |
3 |
5 |
8 |
12 |
16 |
|
|
0,90 |
0,95 |
5 |
8 |
13 |
19 |
26 |
|
|
0,95 |
0,975 |
6 |
11 |
18 |
26 |
38 |
|
|
0,98 |
0,99 |
8 |
15 |
25 |
37 |
52 |
|
0,15 |
- |
0,80 |
1 |
2 |
3 |
4 |
4 |
|
|
0,80 |
0,90 |
3 |
3 |
5 |
6 |
8 |
|
|
0,90 |
0,95 |
4 |
5 |
7 |
10 |
13 |
|
|
0,95 |
0,975 |
5 |
6 |
10 |
13 |
18 |
|
|
0,98 |
0,99 |
6 |
8 |
13 |
18 |
25 |
|
0,20 |
- |
0,80 |
1 |
1 |
2 |
3 |
3 |
|
|
0,80 |
0,90 |
3 |
3 |
4 |
4 |
6 |
|
|
0,90 |
0,95 |
3 |
4 |
5 |
7 |
8 |
|
|
0,95 |
0,975 |
4 |
5 |
6 |
9 |
11 |
|
|
0,98 |
0,99 |
5 |
7 |
8 |
12 |
16 |
Примечание. Число объектов испытаний получено как решение уравнения
.
Таблица 6
Число объектов при плане и распределении Вейбулла при планировании
по предельной относительной ошибке
|
|
|
|
| ||||||
|
|
|
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
0,05 |
- |
0,80 |
48 |
65 |
100 |
150 |
200 |
250 |
315 |
|
|
0,80 |
0,90 |
105 |
200 |
250 |
400 |
500 |
500 |
650 |
|
|
0,90 |
0,95 |
170 |
250 |
400 |
500 |
650 |
800 |
1000 |
|
|
0,95 |
0,975 |
235 |
375 |
500 |
1000 |
>1000 |
|
|
|
|
0,98 |
0,99 |
315 |
500 |
800 |
1000 |
>1000 |
|
|
|
0,10 |
- |
0,80 |
13 |
25 |
32 |
50 |
50 |
65 |
100 |
|
|
0,80 |
0,90 |
32 |
50 |
65 |
100 |
125 |
150 |
200 |
|
|
0,90 |
0,95 |
50 |
80 |
100 |
150 |
200 |
250 |
400 |
|
|
0,95 |
0,975 |
65 |
100 |
160 |
215 |
295 |
375 |
450 |
|
|
0,98 |
0,99 |
100 |
150 |
200 |
315 |
400 |
500 |
650 |
|
0,15 |
- |
0,80 |
6 |
10 |
15 |
20 |
25 |
32 |
40 |
|
|
0,80 |
0,90 |
15 |
25 |
32 |
40 |
65 |
80 |
80 |
|
|
0,90 |
0,95 |
25 |
40 |
50 |
80 |
100 |
125 |
150 |
|
|
0,95 |
0,975 |
32 |
50 |
80 |
110 |
140 |
175 |
210 |
|
|
0,98 |
0,99 |
40 |
65 |
100 |
150 |
200 |
250 |
315 |
|
0,20 |
- |
0,80 |
5 |
8 |
10 |
15 |
20 |
20 |
25 |
|
|
0,80 |
0,90 |
10 |
15 |
20 |
32 |
40 |
40 |
50 |
|
|
0,90 |
0,95 |
15 |
25 |
32 |
40 |
50 |
80 |
100 |
|
|
0,95 |
0,975 |
20 |
32 |
47 |
64 |
80 |
110 |
125 |
|
|
0,98 |
0,99 |
25 |
40 |
65 |
80 |
125 |
150 |
150 |
Примечание. Число получено как решения уравнения
.
Таблица 7
Число объектов при плане и распределении Вейбулла при планировании
по нижней доверительной границе
|
|
|
2,7 |
2,1 |
1,7 |
1,45 |
1,26 |
1,1 |
1 |
|
0,05 |
0,80 |
30 |
53 |
84 |
119 |
157 |
207 |
251 |
|
|
0,90 |
77 |
134 |
203 |
282 |
378 |
495 |
500 |
|
|
0,95 |
133 |
221 |
343 |
472 |
500 |
500 |
500 |
|
|
0,99 |
266 |
448 |
500 |
500 |
500 |
500 |
500 |
|
0,10 |
0,80 |
6 |
10 |
17 |
24 |
33 |
45 |
57 |
|
|
0,90 |
16 |
28 |
45 |
63 |
85 |
115 |
139 |
|
|
0,95 |
28 |
48 |
76 |
107 |
144 |
190 |
231 |
|
|
0,99 |
59 |
100 |
156 |
218 |
290 |
385 |
468 |
|
0,15 |
0,80 |
2 |
3 |
6 |
9 |
12 |
18 |
21 |
|
|
0,90 |
6 |
11 |
17 |
25 |
33 |
45 |
55 |
|
|
0,95 |
11 |
19 |
30 |
42 |
57 |
76 |
94 |
|
|
0,99 |
23 |
40 |
62 |
88 |
121 |
157 |
191 |
|
0,20 |
0,80 |
1 |
1 |
3 |
4 |
6 |
8 |
10 |
|
|
0,90 |
3 |
5 |
8 |
12 |
17 |
22 |
28 |
|
|
0,95 |
5 |
9 |
15 |
21 |
29 |
39 |
48 |
|
|
0,99 |
11 |
20 |
31 |
60 |
|
81 |
98 |
Примечание. Число объектов испытаний получено как решение уравнения
.
Таблица 8
Число объектов при плане и логарифмически нормальном распределении
|
|
|
|
| ||||||
|
|
|
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
0,05 |
- |
0,80 |
40 |
65 |
100 |
125 |
150 |
200 |
250 |
|
|
0,80 |
0,90 |
100 |
150 |
250 |
315 |
400 |
500 |
650 |
|
|
0,90 |
0,95 |
150 |
250 |
400 |
500 |
650 |
800 |
1000 |
|
|
0,95 |
0,975 |
245 |
381 |
546 |
735 |
949 |
>1000 |
|
|
|
0,98 |
0,99 |
315 |
500 |
800 |
>1000 |
|
|
|
|
0,10 |
- |
0,80 |
10 |
20 |
25 |
32 |
40 |
50 |
65 |
|
|
0,80 |
0,90 |
25 |
40 |
65 |
80 |
100 |
125 |
150 |
|
|
0,90 |
0,95 |
40 |
65 |
100 |
125 |
150 |
200 |
250 |
|
|
0,95 |
0,975 |
62 |
96 |
137 |
184 |
238 |
296 |
359 |
|
|
0,98 |
0,99 |
80 |
125 |
200 |
250 |
315 |
400 |
500 |
|
0,15 |
- |
0,80 |
5 |
8 |
10 |
15 |
20 |
25 |
32 |
|
|
0,80 |
0,90 |
13 |
20 |
25 |
40 |
50 |
50 |
65 |
|
|
0,90 |
0,95 |
20 |
32 |
40 |
50 |
80 |
100 |
100 |
|
|
0,95 |
0,975 |
28 |
43 |
61 |
82 |
106 |
132 |
160 |
|
|
0,98 |
0,99 |
40 |
50 |
80 |
125 |
150 |
200 |
200 |
|
0,20 |
- |
0,80 |
3 |
4 |
6 |
8 |
10 |
15 |
20 |
|
|
0,80 |
0,90 |
6 |
10 |
15 |
20 |
25 |
32 |
40 |
|
|
0,90 |
0,95 |
10 |
15 |
25 |
32 |
40 |
50 |
65 |
|
|
0,95 |
0,975 |
16 |
24 |
35 |
46 |
60 |
74 |
90 |
|
|
0,98 |
0,99 |
20 |
32 |
50 |
65 |
80 |
100 |
125 |
Примечание. 
.
Таблица 9
Число объектов при плане и диффузионном распределении
|
|
|
|
| |||||||||
|
|
|
|
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,2 |
1,5 |
|
0,05 |
- |
0,80 |
26 |
45 |
71 |
102 |
139 |
181 |
230 |
283 |
408 |
638 |
|
|
0,80 |
0,90 |
59 |
105 |
164 |
237 |
322 |
421 |
533 |
658 |
947 |
>1000 |
|
|
0,90 |
0,95 |
99 |
175 |
274 |
395 |
537 |
702 |
868 |
>1000 |
|
|
|
|
0,95 |
0,975 |
138 |
246 |
384 |
554 |
753 |
984 |
>1000 |
|
|
|
|
|
0,98 |
0,99 |
195 |
347 |
542 |
780 |
>1000 |
|
|
|
|
|
|
0,10 |
- |
0,80 |
6 |
11 |
18 |
26 |
35 |
45 |
58 |
71 |
102 |
160 |
|
|
0,80 |
0,90 |
15 |
26 |
41 |
59 |
81 |
105 |
133 |
165 |
237 |
371 |
|
|
0,90 |
0,95 |
25 |
44 |
69 |
99 |
135 |
176 |
222 |
275 |
395 |
618 |
|
|
0,95 |
0,975 |
35 |
62 |
96 |
139 |
189 |
246 |
312 |
385 |
555 |
867 |
|
|
0,98 |
0,99 |
49 |
87 |
136 |
195 |
266 |
347 |
439 |
543 |
781 |
1000 |
|
0,15 |
- |
0,80 |
3 |
5 |
8 |
11 |
16 |
20 |
26 |
32 |
46 |
71 |
|
|
0,80 |
0,90 |
7 |
12 |
18 |
26 |
36 |
47 |
59 |
73 |
106 |
165 |
|
|
0,90 |
0,95 |
11 |
20 |
31 |
44 |
60 |
78 |
99 |
122 |
176 |
275 |
|
|
0,95 |
0,975 |
15 |
27 |
43 |
62 |
84 |
110 |
139 |
172 |
247 |
386 |
|
|
0,98 |
0,99 |
22 |
39 |
60 |
87 |
119 |
155 |
196 |
242 |
348 |
544 |
|
0,20 |
- |
0,80 |
2 |
3 |
4 |
6 |
9 |
11 |
14 |
18 |
26 |
40 |
|
|
0,80 |
0,90 |
4 |
7 |
10 |
15 |
20 |
27 |
34 |
41 |
60 |
93 |
|
|
0,90 |
0,95 |
6 |
11 |
17 |
25 |
34 |
44 |
56 |
69 |
100 |
156 |
|
|
0,95 |
0,975 |
9 |
16 |
24 |
35 |
48 |
62 |
79 |
97 |
140 |
218 |
Примечание. 
.
Таблица 10
Число объектов при плане и =10 для нормального распределения
|
|
|
|
| ||||
|
|
|
|
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
|
0,05 |
- |
0,80 |
2 |
4 |
5 |
6 |
7 |
|
|
0,80 |
0,90 |
4 |
6 |
7 |
8 |
9 |
|
|
0,90 |
0,95 |
5 |
7 |
8 |
9 |
9 |
|
|
0,95 |
0,975 |
6 |
8 |
9 |
9 |
9 |
|
|
0,98 |
0,99 |
7 |
8 |
9 |
9 |
10 |
|
0,10 |
- |
0,80 |
1 |
1 |
2 |
3 |
4 |
|
|
0,80 |
0,90 |
1 |
3 |
4 |
5 |
6 |
|
|
0,90 |
0,95 |
2 |
4 |
5 |
6 |
7 |
|
|
0,95 |
0,975 |
3 |
5 |
6 |
7 |
8 |
|
|
0,98 |
0,99 |
4 |
5 |
7 |
8 |
8 |
|
0,15 |
- |
0,80 |
1 |
1 |
1 |
2 |
2 |
|
|
0,80 |
0,90 |
1 |
1 |
2 |
3 |
4 |
|
|
0,90 |
0,95 |
1 |
2 |
3 |
4 |
5 |
|
|
0,95 |
0,975 |
1 |
3 |
4 |
5 |
6 |
|
|
0,98 |
0,99 |
2 |
4 |
5 |
6 |
7 |
|
0,20 |
- |
0,80 |
1 |
1 |
1 |
1 |
1 |
|
|
0,80 |
0,90 |
1 |
1 |
1 |
2 |
3 |
|
|
0,90 |
0,95 |
1 |
1 |
2 |
3 |
4 |
|
|
0,95 |
0,975 |
1 |
2 |
3 |
4 |
5 |
|
|
0,98 |
0,99 |
1 |
2 |
4 |
5 |
5 |
Примечание к табл.10-14:
.
Таблица 11
Число объектов при плане и =20 для нормального распределения
|
|
|
|
| ||||
|
|
|
|
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
|
0,05 |
- |
0,80 |
2 |
5 |
7 |
9 |
11 |
|
|
0,80 |
0,90 |
5 |
9 |
11 |
13 |
15 |
|
|
0,90 |
0,95 |
7 |
11 |
14 |
15 |
17 |
|
|
0,95 |
0,975 |
9 |
13 |
15 |
17 |
17 |
|
|
0,98 |
0,99 |
10 |
14 |
16 |
17 |
18 |
|
0,10 |
- |
0,80 |
1 |
1 |
2 |
4 |
5 |
|
|
0,80 |
0,90 |
2 |
3 |
5 |
7 |
9 |
|
|
0,90 |
0,95 |
2 |
5 |
7 |
9 |
11 |
|
|
0,95 |
0,975 |
3 |
6 |
9 |
11 |
13 |
|
|
0,98 |
0,99 |
4 |
8 |
10 |
13 |
14 |
|
0,15 |
- |
0,80 |
1 |
1 |
1 |
2 |
2 |
|
|
0,80 |
0,90 |
1 |
2 |
3 |
4 |
5 |
|
|
0,90 |
0,95 |
1 |
2 |
4 |
5 |
7 |
|
|
0,95 |
0,975 |
2 |
3 |
5 |
7 |
9 |
|
|
0,98 |
0,99 |
2 |
4 |
6 |
9 |
10 |
|
0,20 |
- |
0,80 |
1 |
1 |
1 |
1 |
1 |
|
|
0,80 |
0,90 |
1 |
1 |
2 |
2 |
3 |
|
|
0,90 |
0,95 |
1 |
1 |
2 |
3 |
5 |
|
|
0,95 |
0,975 |
1 |
2 |
3 |
5 |
6 |
|
|
0,98 |
0,99 |
1 |
3 |
4 |
6 |
8 |
Таблица 12
Число объектов при плане и =30 для нормального распределения
|
|
|
|
| ||||
|
|
|
|
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
|
0,05 |
- |
0,80 |
3 |
5 |
8 |
11 |
14 |
|
|
0,80 |
0,90 |
5 |
10 |
14 |
17 |
20 |
|
|
0,90 |
0,95 |
8 |
13 |
18 |
21 |
23 |
|
|
0,95 |
0,975 |
10 |
16 |
20 |
23 |
25 |
|
|
0,98 |
0,99 |
13 |
19 |
22 |
25 |
26 |
|
0,10 |
- |
0,80 |
1 |
2 |
3 |
4 |
5 |
|
|
0,80 |
0,90 |
2 |
3 |
5 |
8 |
10 |
|
|
0,90 |
0,95 |
2 |
5 |
8 |
11 |
13 |
|
|
0,95 |
0,975 |
3 |
7 |
10 |
13 |
16 |
|
|
0,98 |
0,99 |
5 |
9 |
13 |
16 |
19 |
|
0,15 |
- |
0,80 |
1 |
1 |
1 |
2 |
3 |
|
|
0,80 |
0,90 |
1 |
2 |
3 |
4 |
5 |
|
|
0,90 |
0,95 |
1 |
2 |
4 |
6 |
8 |
|
|
0,95 |
0,975 |
2 |
3 |
6 |
8 |
10 |
|
|
0,98 |
0,99 |
2 |
5 |
7 |
10 |
13 |
|
0,20 |
- |
0,80 |
1 |
1 |
1 |
1 |
2 |
|
|
0,80 |
0,90 |
1 |
1 |
2 |
2 |
3 |
|
|
0,90 |
0,95 |
1 |
1 |
2 |
4 |
5 |
|
|
0,95 |
0,975 |
1 |
2 |
3 |
5 |
7 |
|
|
0,98 |
0,99 |
1 |
3 |
5 |
7 |
9 |
Таблица 13
Число объектов при плане и = 40 для нормального распределения
|
|
|
|
| ||||
|
|
|
|
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
|
0,05 |
- |
0,80 |
3 |
6 |
9 |
12 |
16 |
|
|
0,80 |
0,90 |
6 |
11 |
16 |
20 |
24 |
|
|
0,90 |
0,95 |
9 |
15 |
21 |
25 |
28 |
|
|
0,95 |
0,975 |
11 |
19 |
24 |
28 |
31 |
|
|
0,98 |
0,99 |
14 |
22 |
27 |
31 |
33 |
|
0,10 |
- |
0,80 |
1 |
2 |
3 |
4 |
6 |
|
|
0,80 |
0,90 |
2 |
3 |
6 |
8 |
11 |
|
|
0,90 |
0,95 |
3 |
5 |
9 |
12 |
15 |
|
|
0,95 |
0,975 |
4 |
7 |
11 |
15 |
19 |
|
|
0,98 |
0,99 |
5 |
9 |
14 |
18 |
22 |
|
0,15 |
- |
0,80 |
1 |
1 |
1 |
2 |
3 |
|
|
0,80 |
0,90 |
1 |
2 |
3 |
4 |
6 |
|
|
0,90 |
0,95 |
1 |
3 |
4 |
6 |
9 |
|
|
0,95 |
0,975 |
2 |
4 |
6 |
8 |
11 |
|
|
0,98 |
0,99 |
2 |
5 |
8 |
11 |
14 |
|
0,20 |
- |
0,80 |
1 |
1 |
1 |
1 |
2 |
|
|
0,80 |
0,90 |
1 |
1 |
2 |
2 |
3 |
|
|
0,90 |
0,95 |
1 |
1 |
3 |
4 |
5 |
|
|
0,95 |
0,975 |
1 |
2 |
4 |
5 |
7 |
|
|
0,98 |
0,99 |
1 |
3 |
5 |
7 |
9 |
Таблица 14
Число объектов испытаний при плане и =50 для нормального распределения
|
|
|
|
| ||||
|
|
|
|
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
|
0,05 |
- |
0,80 |
3 |
6 |
9 |
13 |
17 |
|
|
0,80 |
0,90 |
6 |
11 |
17 |
23 |
27 |
|
|
0,90 |
0,95 |
9 |
16 |
23 |
29 |
33 |
|
|
0,95 |
0,975 |
12 |
20 |
28 |
33 |
37 |
|
|
0,98 |
0,99 |
15 |
25 |
32 |
37 |
40 |
|
0,10 |
- |
0,80 |
1 |
2 |
3 |
4 |
6 |
|
|
0,80 |
0,90 |
2 |
3 |
6 |
9 |
11 |
|
|
0,90 |
0,95 |
3 |
5 |
9 |
13 |
16 |
|
|
0,95 |
0,975 |
4 |
7 |
11 |
16 |
20 |
|
|
0,98 |
0,99 |
5 |
10 |
15 |
20 |
25 |
|
0,15 |
- |
0,80 |
1 |
1 |
1 |
2 |
3 |
|
|
0,80 |
0,90 |
1 |
2 |
3 |
4 |
6 |
|
|
0,90 |
0,95 |
1 |
3 |
4 |
7 |
9 |
|
|
0,95 |
0,975 |
2 |
4 |
6 |
9 |
12 |
|
|
0,98 |
0,99 |
2 |
5 |
8 |
12 |
15 |
|
0,20 |
- |
0,80 |
1 |
1 |
1 |
1 |
2 |
|
|
0,80 |
0,90 |
1 |
1 |
2 |
2 |
3 |
|
|
0,90 |
0,95 |
1 |
1 |
3 |
4 |
5 |
|
|
0,95 |
0,975 |
1 |
2 |
4 |
5 |
7 |
|
|
0,98 |
0,99 |
1 |
3 |
5 |
7 |
10 |
Таблица 15
Число объектов испытаний при плане и =10 для распределения Вейбулла
|
|
|
|
| ||||||
|
|
|
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
0,05 |
- |
0,80 |
6 |
7 |
8 |
8 |
8 |
8 |
9 |
|
|
0,80 |
0,90 |
8 |
8 |
9 |
|
|
|
|
|
|
0,90 |
0,95 |
8 |
9 |
|
|
|
|
|
|
|
0,95 |
0,975 |
9 |
|
|
|
|
|
|
|
|
0,98 |
0,99 |
9 |
|
|
|
|
|
|
|
0,10 |
- |
0,80 |
3 |
4 |
5 |
6 |
6 |
7 |
7 |
|
|
0,80 |
0,90 |
5 |
6 |
7 |
7 |
7 |
8 |
8 |
|
|
0,90 |
0,95 |
6 |
7 |
7 |
8 |
8 |
8 |
8 |
|
|
0,95 |
0,975 |
7 |
7 |
8 |
8 |
8 |
8 |
8 |
|
|
0,98 |
0,99 |
7 |
8 |
8 |
8 |
8 |
8 |
8 |
|
0,15 |
- |
0,80 |
2 |
2 |
3 |
4 |
4 |
5 |
5 |
|
|
0,80 |
0,90 |
3 |
4 |
5 |
6 |
6 |
7 |
7 |
|
|
0,90 |
0,95 |
4 |
5 |
6 |
6 |
6 |
7 |
7 |
|
|
0,95 |
0,975 |
5 |
6 |
6 |
7 |
7 |
7 |
7 |
|
|
0,98 |
0,99 |
5 |
6 |
7 |
7 |
8 |
8 |
8 |
|
0,20 |
- |
0,80 |
1 |
1 |
2 |
2 |
3 |
3 |
4 |
|
|
0,80 |
0,90 |
2 |
3 |
3 |
4 |
5 |
5 |
6 |
|
|
0,90 |
0,95 |
3 |
4 |
5 |
5 |
6 |
6 |
6 |
|
|
0,95 |
0,975 |
4 |
4 |
5 |
6 |
6 |
6 |
7 |
|
|
0,98 |
0,99 |
4 |
5 |
5 |
6 |
6 |
7 |
7 |
Примечание к табл.15-19:
.
Таблица 16
Число объектов испытаний при плане и =20 для распределения Вейбулла
|
|
|
|
| ||||||
|
|
|
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
0,05 |
- |
0,80 |
10 |
131** |
14 |
15 |
16 |
16 |
17 |
|
|
0,80 |
0,90 |
14 |
16 |
17 |
17 |
17 |
18 |
|
|
|
0,90 |
0,95 |
16 |
17 |
17 |
18 |
|
|
|
|
|
0,95 |
0,975 |
16 |
17 |
17 |
18 |
|
|
|
|
|
0,98 |
0,99 |
17 |
18 |
|
|
|
|
|
|
0,10 |
- |
0,80 |
4 |
6 |
8 |
9 |
10 |
12 |
13 |
|
|
0,80 |
0,90 |
8 |
10 |
12 |
13 |
14 |
15 |
15 |
|
|
0,90 |
0,95 |
10 |
1213** |
13 |
14 |
15 |
16 |
16 |
|
|
0,95 |
0,975 |
11 |
13 |
14 |
15 |
16 |
16 |
16 |
|
|
0,98 |
0,99 |
13 |
14 |
15 |
16 |
16 |
17 |
|
|
0,15 |
- |
0,80 |
2 |
2 |
4 |
5 |
6 |
8 |
8 |
|
|
0,80 |
0,90 |
4 |
6 |
8 |
9 |
10 |
11 |
12 |
|
|
0,90 |
0,95 |
6 |
8 |
10 |
11 |
12 |
13 |
14 |
|
|
0,95 |
0,975 |
8 |
10 |
11 |
12 |
13 |
14 |
14 |
|
|
0,98 |
0,99 |
9 |
11 |
12 |
13 |
14 |
14 |
15 |
|
0,20 |
- |
0,80 |
1 |
1 |
2 |
3 |
4 |
5 |
5 |
|
|
0,80 |
0,90 |
2 |
4 |
5 |
6 |
8 |
8 |
9 |
|
|
0,90 |
0,95 |
4 |
5 |
7 |
8 |
9 |
10 |
11 |
|
|
0,95 |
0,975 |
5 |
7 |
8 |
10 |
11 |
11 |
12 |
|
|
0,98 |
0,99 |
6 |
8 |
9 |
11 |
12 |
12 |
13 |
_______________
** Соответствует оригиналу. - Примечание .
Таблица 17
Число объектов испытаний при плане и =30 для распределения Вейбулла
|
|
|
|
| ||||||
|
|
|
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
0,05 |
- |
0,80 |
13 |
17 |
20 |
22 |
23 |
24 |
24 |
|
|
0,80 |
0,90 |
19 |
23 |
24 |
25 |
26 |
26 |
26 |
|
|
0,90 |
0,95 |
23 |
24 |
25 |
26 |
26 |
26 |
27 |
|
|
0,95 |
0,975 |
24 |
25 |
26 |
26 |
27 |
|
|
|
|
0,98 |
0,99 |
24 |
26 |
26 |
27 |
|
|
|
|
0,10 |
- |
0,80 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
|
|
0,80 |
0,90 |
9 |
13 |
16 |
18 |
19 |
21 |
22 |
|
|
0,90 |
0,95 |
13 |
16 |
18 |
20 |
22 |
23 |
23 |
|
|
0,95 |
0,975 |
15 |
18 |
20 |
21 |
23 |
23 |
24 |
|
|
0,98 |
0,99 |
17 |
20 |
22 |
23 |
24 |
24 |
25 |
|
0,15 |
- |
0,80 |
2 |
2 |
4 |
6 |
7 |
10 |
10 |
|
|
0,80 |
0,90 |
5 |
7 |
9 |
12 |
13 |
15 |
16 |
|
|
0,90 |
0,95 |
7 |
10 |
13 |
15 |
16 |
18 |
19 |
|
|
0,95 |
0,975 |
9 |
12 |
15 |
17 |
18 |
19 |
20 |
|
|
0,98 |
0,99 |
11 |
14 |
17 |
18 |
20 |
21 |
21 |
|
0,20 |
- |
0,80 |
1 |
3 |
3 |
3 |
5 |
5 |
6 |
|
|
0,80 |
0,90 |
2 |
4 |
6 |
7 |
9 |
10 |
12 |
|
|
0,90 |
0,95 |
4 |
6 |
9 |
10 |
12 |
14 |
15 |
|
|
0,95 |
0,975 |
6 |
8 |
10 |
12 |
14 |
16 |
16 |
|
|
0,98 |
0,99 |
7 |
10 |
12 |
14 |
16 |
17 |
18 |
Таблица 18
Число объектов испытаний при плане и =40 для распределения Вейбулла
|
|
|
|
| ||||||
|
|
|
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
0,05 |
- |
0,80 |
15 |
21 |
25 |
27 |
29 |
30 |
31 |
|
|
0,80 |
0,90 |
24 |
29 |
31 |
32 |
33 |
34 |
34 |
|
|
0,90 |
0,95 |
30 |
31 |
33 |
34 |
35 |
35 |
35 |
|
|
0,95 |
0,975 |
30 |
32 |
34 |
35 |
35 |
35 |
36 |
|
|
0,98 |
0,99 |
32 |
34 |
35 |
35 |
35 |
36 |
36 |
|
0,10 |
- |
0,80 |
5 |
7 |
11 |
13 |
16 |
18 |
21 |
|
|
0,80 |
0,90 |
10 |
15 |
19 |
22 |
24 |
26 |
27 |
|
|
0,90 |
0,95 |
15 |
19 |
23 |
26 |
28 |
29 |
30 |
|
|
0,95 |
0,975 |
18 |
22 |
25 |
27 |
29 |
30 |
31 |
|
|
0,98 |
0,99 |
21 |
25 |
27 |
29 |
31 |
32 |
32 |
|
0,15 |
- |
0,80 |
2 |
3 |
5 |
7 |
8 |
11 |
12 |
|
|
0,80 |
0,90 |
5 |
8 |
11 |
14 |
16 |
18 |
20 |
|
|
0,90 |
0,95 |
8 |
12 |
15 |
17 |
20 |
22 |
24 |
|
|
0,95 |
0,975 |
10 |
14 |
18 |
20 |
22 |
24 |
25 |
|
|
0,98 |
0,99 |
13 |
17 |
20 |
23 |
25 |
26 |
27 |
|
0,20 |
- |
0,80 |
1 |
1 |
3 |
4 |
5 |
6 |
7 |
|
|
0,80 |
0,90 |
3 |
4 |
6 |
8 |
10 |
12 |
14 |
|
|
0,90 |
0,95 |
4 |
7 |
10 |
12 |
14 |
16 |
18 |
|
|
0,95 |
0,975 |
6 |
9 |
12 |
15 |
17 |
19 |
20 |
|
|
0,98 |
0,99 |
8 |
11 |
14 |
17 |
19 |
21 |
23 |
Таблица 19
Число объектов испытаний при плане и =50 для распределения Вейбулла
|
|
|
|
| ||||||
|
|
|
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
0,05 |
- |
0,80 |
17 |
23 |
29 |
32 |
35 |
37 |
38 |
|
|
0,80 |
0,90 |
28 |
34 |
37 |
39 |
41 |
42 |
42 |
|
|
0,90 |
0,95 |
34 |
37 |
40 |
42 |
43 |
43 |
44 |
|
|
0,95 |
0,975 |
36 |
39 |
42 |
43 |
43 |
44 |
44 |
|
|
0,98 |
0,99 |
38 |
42 |
43 |
44 |
44 |
44 |
45 |
|
0,10 |
- |
0,80 |
5 |
8 |
11 |
14 |
17 |
21 |
24 |
|
|
0,80 |
0,90 |
11 |
16 |
21 |
25 |
28 |
31 |
33 |
|
|
0,90 |
0,95 |
16 |
22 |
26 |
30 |
33 |
35 |
36 |
|
|
0,95 |
0,975 |
20 |
26 |
30 |
33 |
35 |
37 |
38 |
|
|
0,98 |
0,99 |
24 |
29 |
33 |
36 |
37 |
39 |
40 |
|
0,15 |
- |
0,80 |
2 |
3 |
5 |
7 |
9 |
12 |
13 |
|
|
0,80 |
0,90 |
5 |
8 |
12 |
15 |
17 |
21 |
22 |
|
|
0,90 |
0,95 |
9 |
13 |
16 |
20 |
23 |
26 |
28 |
|
|
0,95 |
0,975 |
11 |
16 |
20 |
23 |
26 |
29 |
30 |
|
|
0,98 |
0,99 |
14 |
19 |
24 |
27 |
30 |
32 |
33 |
|
0,20 |
- |
0,80 |
1 |
1 |
3 |
4 |
5 |
6 |
7 |
|
|
0,80 |
0,90 |
3 |
4 |
6 |
9 |
11 |
13 |
16 |
|
|
0,90 |
0,95 |
4 |
7 |
11 |
13 |
16 |
18 |
21 |
|
|
0,95 |
0,975 |
6 |
10 |
13 |
16 |
19 |
22 |
24 |
|
|
0,98 |
0,99 |
8 |
13 |
16 |
20 |
22 |
25 |
27 |
Таблица 20
Число объектов испытаний для оценки гамма-процентных показателей при плане
и нормальном распределении (
=80%)
|
|
|
|
| ||||
|
|
|
|
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
|
0,05 |
- |
0,80 |
7 |
17 |
34 |
58 |
94 |
|
|
0,80 |
0,90 |
16 |
40 |
78 |
135 |
217 |
|
|
0,90 |
0,95 |
27 |
65 |
128 |
222 |
356 |
|
|
0,95 |
0,975 |
38 |
93 |
182 |
315 |
506 |
|
|
0,98 |
0,99 |
53 |
130 |
256 |
443 |
712 |
|
0,10 |
- |
0,80 |
2 |
5 |
9 |
15 |
24 |
|
|
0,80 |
0,90 |
4 |
10 |
20 |
34 |
55 |
|
|
0,90 |
0,95 |
7 |
17 |
32 |
56 |
89 |
|
|
0,95 |
0,975 |
10 |
24 |
46 |
79 |
127 |
|
|
0,98 |
0,99 |
14 |
33 |
64 |
111 |
178 |
|
0,15 |
- |
0,80 |
1 |
2 |
4 |
7 |
11 |
|
|
0,80 |
0,90 |
2 |
5 |
9 |
15 |
25 |
|
|
0,90 |
0,95 |
3 |
8 |
15 |
25 |
40 |
|
|
0,95 |
0,975 |
5 |
11 |
21 |
35 |
57 |
|
|
0,98 |
0,99 |
6 |
15 |
29 |
50 |
80 |
|
0,20 |
- |
0,80 |
1 |
2 |
3 |
4 |
6 |
|
|
0,80 |
0,90 |
1 |
3 |
5 |
9 |
14 |
|
|
0,90 |
0,95 |
2 |
5 |
8 |
14 |
23 |
|
|
0,95 |
0,975 |
3 |
6 |
12 |
20 |
32 |
|
|
0,98 |
0,99 |
4 |
9 |
16 |
28 |
45 |
Примечание к табл.20 и 21:
;
;
.
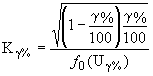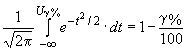Таблица 21
Число объектов испытаний для оценки гамма-процентных показателей
при плане и нормальном распределении (=90%)
|
|
|
|
| ||||
|
|
|
|
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
|
0,05 |
- |
0,80 |
11 |
29 |
60 |
112 |
196 |
|
|
0,80 |
0,90 |
26 |
66 |
139 |
260 |
455 |
|
|
0,90 |
0,95 |
42 |
109 |
228 |
427 |
749 |
|
|
0,95 |
0,975 |
59 |
155 |
324 |
606 |
1064 |
|
|
0,98 |
0,99 |
83 |
218 |
456 |
853 |
1498 |
|
0,10 |
- |
0,80 |
3 |
8 |
15 |
28 |
49 |
|
|
0,80 |
0,90 |
7 |
17 |
35 |
65 |
114 |
|
|
0,90 |
0,95 |
11 |
28 |
57 |
107 |
188 |
|
|
0,95 |
0,975 |
15 |
39 |
81 |
152 |
266 |
|
|
0,98 |
0,99 |
21 |
55 |
114 |
214 |
375 |
|
0,15 |
- |
0,80 |
2 |
4 |
7 |
13 |
22 |
|
|
0,80 |
0,90 |
3 |
8 |
16 |
29 |
51 |
|
|
0,90 |
0,95 |
5 |
13 |
26 |
48 |
84 |
|
|
0,95 |
0,975 |
7 |
18 |
36 |
68 |
119 |
|
|
0,98 |
0,99 |
10 |
25 |
51 |
95 |
167 |
|
0,20 |
- |
0,80 |
1 |
2 |
4 |
7 |
13 |
|
|
0,80 |
0,90 |
2 |
5 |
9 |
17 |
29 |
|
|
0,90 |
0,95 |
3 |
7 |
15 |
27 |
47 |
|
|
0,95 |
0,975 |
4 |
10 |
21 |
38 |
67 |
|
|
0,98 |
0,99 |
6 |
14 |
29 |
54 |
94 |
Таблица 22
Число объектов испытаний для оценки гамма-процентных показателей
надежности при плане и распределении Вейбулла (=80%)
|
|
|
|
| ||||||
|
|
|
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
0,05 |
- |
0,80 |
196 |
323 |
493 |
677 |
896 |
>1000 |
|
|
|
0,80 |
0,90 |
453 |
749 |
>1000 |
|
|
|
|
|
|
0,90 |
0,95 |
746 |
>1000 |
|
|
|
|
|
|
|
0,95 |
0,975 |
>1000 |
|
|
|
|
|
|
|
|
0,98 |
0,99 |
>1000 |
|
|
|
|
|
|
|
0,10 |
- |
0,80 |
49 |
81 |
124 |
170 |
224 |
294 |
356 |
|
|
0,80 |
0,90 |
114 |
188 |
286 |
393 |
520 |
682 |
826 |
|
|
0,90 |
0,95 |
187 |
309 |
471 |
647 |
856 |
>1000 |
|
|
|
0,95 |
0,975 |
265 |
438 |
668 |
918 |
>1000 |
|
|
|
|
0,98 |
0,99 |
373 |
616 |
940 |
>1000 |
|
|
|
|
0,15 |
- |
0,80 |
22 |
36 |
55 |
76 |
100 |
131 |
159 |
|
|
0,80 |
0,90 |
51 |
84 |
127 |
175 |
231 |
304 |
367 |
|
|
0,90 |
0,95 |
83 |
137 |
209 |
288 |
381 |
500 |
604 |
|
|
0,95 |
0,975 |
118 |
195 |
297 |
408 |
540 |
709 |
658 |
|
|
0,98 |
0,99 |
166 |
274 |
418 |
575 |
761 |
998 |
>1000 |
|
0,20 |
- |
0,80 |
13 |
21 |
31 |
43 |
56 |
74 |
89 |
|
|
0,80 |
0,90 |
29 |
47 |
72 |
99 |
130 |
171 |
207 |
|
|
0,90 |
0,95 |
47 |
77 |
118 |
162 |
214 |
281 |
343 |
|
|
0,95 |
0,975 |
67 |
110 |
167 |
230 |
304 |
399 |
480 |
|
|
0,98 |
0,99 |
94 |
154 |
235 |
323 |
428 |
502 |
580 |
Примечание к табл.22 и 23:
; 
.
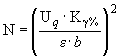Таблица 23
Число объектов испытаний для оценки гамма-процентных показателей
надежности при плане и распределении Вейбулла (=90%)
|
|
|
|
| ||||||
|
|
|
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
0,05 |
- |
0,80 |
392 |
646 |
986 |
>1000 |
|
|
|
|
|
0,80 |
0,90 |
906 |
>1000 |
|
|
|
|
|
|
|
0,90 |
0,95 |
>1000 |
|
|
|
|
|
|
|
|
0,95 |
0,975 |
>1000 |
|
|
|
|
|
|
|
|
0,98 |
0,99 |
>1000 |
|
|
|
|
|
|
|
0,10 |
- |
0,80 |
98 |
162 |
248 |
340 |
448 |
588 |
712 |
|
|
0,80 |
0,90 |
228 |
376 |
572 |
786 |
>1000 |
|
|
|
|
0,90 |
0,95 |
374 |
618 |
942 |
>1000 |
|
|
|
|
|
0,95 |
0,975 |
530 |
876 |
>1000 |
|
|
|
|
|
|
0,98 |
0,99 |
746 |
>1000 |
|
|
|
|
|
|
0,15 |
- |
0,80 |
44 |
72 |
110 |
152 |
200 |
262 |
318 |
|
|
0,80 |
0,90 |
102 |
168 |
254 |
350 |
462 |
608 |
734 |
|
|
0,90 |
0,95 |
166 |
274 |
418 |
576 |
762 |
>1000 |
|
|
|
0,95 |
0,975 |
236 |
390 |
594 |
816 |
>1000 |
|
|
|
|
0,98 |
0,99 |
332 |
548 |
836 |
>1000 |
|
|
|
|
0,20 |
- |
0,80 |
26 |
42 |
62 |
86 |
112 |
148 |
178 |
|
|
0,80 |
0,90 |
58 |
94 |
144 |
198 |
260 |
342 |
414 |
|
|
0,90 |
0,95 |
94 |
154 |
236 |
324 |
418 |
562 |
680 |
|
|
0,95 |
0,975 |
134 |
220 |
334 |
460 |
608 |
798 |
966 |
|
|
0,98 |
0,99 |
188 |
308 |
470 |
646 |
856 |
>1000 |
|
Таблица 24
Число объектов испытаний для оценки гамма-процентных показателей надежности
при плане и логарифмически нормальном распределении (=80%)
|
|
|
|
| ||||||
|
|
|
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
0,05 |
- |
0,80 |
86 |
129 |
178 |
231 |
287 |
344 |
402 |
|
|
0,80 |
0,90 |
200 |
300 |
413 |
536 |
665 |
798 |
932 |
|
|
0,90 |
0,95 |
329 |
494 |
681 |
883 |
>1000 |
|
|
|
|
0,95 |
0,975 |
466 |
701 |
966 |
>1000 |
|
|
|
|
|
0,98 |
0,99 |
658 |
989 |
>1000 |
|
|
|
|
|
0,10 |
- |
0,80 |
22 |
32 |
45 |
58 |
72 |
86 |
100 |
|
|
0,80 |
0,90 |
50 |
75 |
103 |
134 |
166 |
199 |
233 |
|
|
0,90 |
0,95 |
82 |
123 |
170 |
221 |
274 |
328 |
384 |
|
|
0,95 |
0,975 |
117 |
175 |
242 |
313 |
389 |
466 |
545 |
|
|
0,98 |
0,99 |
164 |
247 |
341 |
442 |
548 |
658 |
768 |
|
0,15 |
- |
0,80 |
10 |
14 |
20 |
26 |
32 |
38 |
45 |
|
|
0,80 |
0,90 |
22 |
33 |
46 |
60 |
74 |
89 |
104 |
|
|
0,90 |
0,95 |
37 |
55 |
76 |
98 |
122 |
146 |
170 |
|
|
0,95 |
0,975 |
52 |
78 |
107 |
139 |
173 |
207 |
242 |
|
|
0,98 |
0,99 |
73 |
110 |
151 |
196 |
244 |
292 |
341 |
|
0,20 |
- |
0,80 |
5 |
8 |
11 |
14 |
18 |
22 |
25 |
|
|
0,80 |
0,90 |
12 |
19 |
26 |
34 |
42 |
50 |
58 |
|
|
0,90 |
0,95 |
21 |
31 |
43 |
55 |
68 |
82 |
96 |
|
|
0,95 |
0,975 |
29 |
44 |
60 |
78 |
97 |
117 |
136 |
|
|
0,98 |
0,99 |
41 |
62 |
85 |
110 |
137 |
164 |
192 |
Примечание к табл.24 и 25:
,
.
Таблица 25
Число объектов испытаний для оценки гамма-процентных показателей надежности
при плане и логарифмически нормальном распределении (=90%)
|
|
|
|
| ||||||
|
|
|
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
0,05 |
- |
0,80 |
123 |
185 |
255 |
331 |
410 |
492 |
575 |
|
|
0,80 |
0,90 |
285 |
429 |
591 |
767 |
951 |
>1000 |
|
|
|
0,90 |
0,95 |
470 |
706 |
973 |
>1000 |
|
|
|
|
|
0,95 |
0,975 |
667 |
>1000 |
|
|
|
|
|
|
|
0,98 |
0,99 |
941 |
>1000 |
|
|
|
|
|
|
0,10 |
- |
0,80 |
31 |
46 |
64 |
83 |
103 |
123 |
144 |
|
|
0,80 |
0,90 |
71 |
107 |
148 |
192 |
238 |
285 |
333 |
|
|
0,90 |
0,95 |
117 |
177 |
243 |
316 |
391 |
469 |
548 |
|
|
0,95 |
0,975 |
167 |
251 |
345 |
448 |
556 |
666 |
779 |
|
|
0,98 |
0,99 |
235 |
354 |
487 |
632 |
784 |
940 |
>1000 |
|
0,15 |
- |
0,80 |
14 |
21 |
28 |
37 |
46 |
55 |
64 |
|
|
0,80 |
0,90 |
32 |
48 |
66 |
85 |
106 |
127 |
148 |
|
|
0,90 |
0,95 |
52 |
78 |
108 |
140 |
174 |
209 |
244 |
|
|
0,95 |
0,975 |
74 |
111 |
154 |
199 |
247 |
296 |
346 |
|
|
0,98 |
0,99 |
105 |
157 |
217 |
281 |
348 |
418 |
488 |
|
0,20 |
- |
0,80 |
8 |
12 |
16 |
21 |
26 |
31 |
36 |
|
|
0,80 |
0,90 |
18 |
27 |
37 |
48 |
59 |
71 |
83 |
|
|
0,90 |
0,95 |
29 |
44 |
61 |
79 |
98 |
117 |
137 |
|
|
0,95 |
0,975 |
42 |
63 |
86 |
112 |
139 |
167 |
195 |
|
|
0,98 |
0,99 |
59 |
88 |
122 |
158 |
196 |
235 |
275 |
Таблица 26
Число отказов испытаний для плана при оценке гамма-процентных показателей надежности
|
|
|
| ||||||||||||||
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
8 |
10 |
15 |
20 |
25 |
32 |
40 |
50 |
|
0,50 |
0,80 |
- |
- |
- |
8 |
10 |
13 |
13 |
20 |
25 |
32 |
40 |
50 |
65 |
80 |
100 |
|
|
0,90 |
- |
- |
6 |
8 |
10 |
13 |
15 |
20 |
25 |
32 |
40 |
50 |
65 |
80 |
100 |
|
|
0,95 |
- |
- |
8 |
10 |
13 |
15 |
20 |
25 |
32 |
40 |
50 |
65 |
80 |
100 |
125 |
|
|
0,99 |
6 |
10 |
10 |
13 |
15 |
20 |
20 |
25 |
32 |
50 |
65 |
65 |
80 |
100 |
125 |
|
0,80 |
0,80 |
8 |
8 |
13 |
20 |
25 |
32 |
40 |
50 |
65 |
80 |
125 |
150 |
150 |
200 |
- |
|
|
0,90 |
10 |
10 |
15 |
25 |
32 |
40 |
40 |
50 |
65 |
100 |
125 |
150 |
200 |
- |
- |
|
|
0,95 |
13 |
13 |
20 |
32 |
40 |
40 |
50 |
65 |
80 |
100 |
125 |
150 |
200 |
- |
- |
|
|
0,99 |
20 |
20 |
25 |
32 |
40 |
50 |
50 |
65 |
80 |
125 |
150 |
150 |
200 |
- |
- |
|
0,90 |
0,80 |
15 |
15 |
32 |
40 |
50 |
65 |
80 |
100 |
125 |
200 |
200 |
200 |
- |
- |
- |
|
|
0,90 |
20 |
20 |
32 |
50 |
65 |
80 |
80 |
100 |
150 |
200 |
200 |
- |
- |
- |
- |
|
|
0,95 |
20 |
25 |
40 |
50 |
65 |
80 |
100 |
125 |
150 |
200 |
- |
- |
- |
- |
- |
|
|
0,99 |
32 |
50 |
80 |
80 |
100 |
125 |
125 |
150 |
200 |
- |
- |
- |
- |
- |
- |
|
0,95 |
0,80 |
32 |
32 |
50 |
80 |
100 |
125 |
150 |
150 |
200 |
- |
- |
- |
- |
- |
- |
|
|
0,90 |
50 |
50 |
65 |
100 |
100 |
125 |
150 |
200 |
- |
- |
- |
- |
- |
- |
- |
|
|
0,95 |
50 |
65 |
80 |
125 |
150 |
200 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
0,99 |
65 |
65 |
100 |
125 |
150 |
150 |
200 |
- |
- |
- |
- |
- |
- |
- |
- |
Таблица 27
Число отказов для планов 
, 
, 
, 
|
|
| |||
|
|
0,80 |
0,90 |
0,95 |
0,99 |
|
0,05 |
331/251 |
>500/>500 |
>500/>500 |
>500/>500 |
|
0,10 |
88/57 |
217/139 |
346/231 |
>500/468 |
|
0,15 |
56/21 |
114/55 |
170/94 |
358/191 |
|
0,20 |
29/10 |
59/28 |
116/48 |
232/98 |
Примечания:
1. Распределение наработки между отказами (до отказа) является экспоненциальным.
2. В числителе приведены значения числа отказов при планировании по предельной относительной ошибке (верхней доверительной границе), в знаменателе - при планировании по нижней доверительной границе.
Таблица 28
Число объектов испытаний для оценки вероятности безотказной работы 
с доверительной вероятностью при допустимом числе отказов
|
|
|
| ||||
|
|
|
0,80 |
0,85 |
0,90 |
0,95 |
0,975 |
|
0 |
0,80 |
7 |
10 |
15 |
31 |
64 |
|
|
0,90 |
10 |
14 |
22 |
45 |
91 |
|
|
0,95 |
13 |
18 |
28 |
58 |
118 |
|
|
0,99 |
21 |
28 |
44 |
90 |
182 |
|
1 |
0,80 |
14 |
19 |
29 |
59 |
119 |
|
|
0,90 |
18 |
25 |
38 |
77 |
154 |
|
|
0,95 |
22 |
30 |
46 |
93 |
188 |
|
|
0,99 |
31 |
42 |
64 |
130 |
263 |
|
2 |
0,80 |
21 |
28 |
42 |
85 |
170 |
|
|
0,90 |
25 |
34 |
52 |
105 |
212 |
|
|
0,95 |
30 |
40 |
61 |
124 |
250 |
|
|
0,99 |
39 |
53 |
81 |
165 |
333 |
|
3 |
0,80 |
27 |
36 |
54 |
109 |
220 |
|
|
0,90 |
32 |
43 |
65 |
132 |
266 |
|
|
0,95 |
37 |
50 |
75 |
153 |
308 |
|
|
0,99 |
47 |
64 |
97 |
198 |
399 |
|
4 |
0,80 |
32 |
44 |
66 |
133 |
268 |
|
|
0,90 |
38 |
52 |
78 |
158 |
318 |
|
|
0,95 |
43 |
59 |
89 |
181 |
364 |
|
|
0,99 |
54 |
74 |
112 |
229 |
461 |
|
5 |
0,80 |
38 |
52 |
78 |
157 |
315 |
|
|
0,90 |
44 |
60 |
91 |
184 |
369 |
|
|
0,95 |
50 |
68 |
103 |
208 |
418 |
|
|
0,99 |
62 |
83 |
127 |
258 |
>500 |
|
6 |
0,80 |
44 |
59 |
89 |
180 |
362 |
|
|
0,90 |
51 |
68 |
103 |
209 |
419 |
|
|
0,95 |
56 |
76 |
116 |
234 |
471 |
|
|
0,99 |
69 |
93 |
142 |
287 |
>500 |
|
7 |
0,80 |
50 |
67 |
101 |
203 |
408 |
|
|
0,90 |
57 |
76 |
116 |
233 |
469 |
|
|
0,95 |
63 |
85 |
129 |
260 |
>500 |
|
|
0,99 |
76 |
102 |
156 |
316 |
>500 |
|
8 |
0,80 |
55 |
74 |
112 |
226 |
454 |
|
|
0,90 |
63 |
84 |
128 |
258 |
>500 |
|
|
0,95 |
69 |
93 |
141 |
286 |
>500 |
|
|
0,99 |
82 |
111 |
170 |
344 |
>500 |
|
9 |
0,80 |
61 |
82 |
124 |
249 |
499 |
|
|
0,90 |
69 |
92 |
140 |
282 |
>500 |
|
|
0,95 |
75 |
102 |
154 |
311 |
>500 |
|
|
0,99 |
89 |
120 |
183 |
371 |
>500 |
|
10 |
0,80 |
67 |
89 |
135 |
271 |
>500 |
|
|
0,90 |
74 |
100 |
152 |
306 |
>500 |
|
|
0,95 |
81 |
110 |
166 |
336 |
>500 |
|
|
0,99 |
96 |
129 |
197 |
398 |
>500 |
Примечание.
, 
;
, 
, 
;
, 
, 
.
Таблица 29
Число отказов при плане для оценки коэффициента готовности при =0,1
|
|
|
| ||||||
|
|
|
0,1 |
0,2 |
0,3 |
0,4 |
0,6 |
0,8 |
1,0 |
|
0,05 |
0,80 |
6 |
15 |
25 |
50 |
100 |
200 |
315 |
|
|
0,90 |
13 |
32 |
65 |
125 |
250 |
400 |
650 |
|
|
0,95 |
20 |
65 |
125 |
200 |
400 |
800 |
1000 |
|
|
0,975 |
29 |
71 |
142 |
284 |
568 |
710 |
1000 |
|
|
0,99 |
40 |
100 |
200 |
400 |
800 |
1000 |
>1000 |
|
0,10 |
0,80 |
3 |
4 |
8 |
15 |
32 |
50 |
80 |
|
|
0,90 |
4 |
10 |
20 |
32 |
65 |
125 |
200 |
|
|
0,95 |
6 |
15 |
32 |
50 |
125 |
200 |
315 |
|
|
0,975 |
7 |
23 |
47 |
70 |
180 |
280 |
465 |
|
|
0,99 |
10 |
32 |
65 |
100 |
250 |
400 |
650 |
|
0,15 |
0,80 |
3 |
3 |
4 |
6 |
15 |
25 |
40 |
|
|
0,90 |
3 |
5 |
10 |
15 |
32 |
65 |
100 |
|
|
0,95 |
3 |
8 |
15 |
25 |
50 |
100 |
150 |
|
|
0,975 |
4 |
11 |
23 |
35 |
90 |
140 |
225 |
|
|
0,99 |
6 |
15 |
32 |
50 |
125 |
200 |
315 |
|
0,20 |
0,80 |
3 |
3 |
3 |
4 |
10 |
15 |
25 |
|
|
0,90 |
3 |
3 |
6 |
10 |
20 |
40 |
65 |
|
|
0,95 |
3 |
5 |
10 |
15 |
32 |
65 |
100 |
|
|
0,975 |
3 |
7 |
14 |
23 |
47 |
90 |
140 |
|
|
0,99 |
3 |
10 |
20 |
32 |
65 |
125 |
200 |
Примечание к табл.29-35:
.
Таблица 30
Число отказов при плане для оценки коэффициента готовности при =0,2
|
|
|
| ||||||
|
|
|
0,1 |
0,2 |
0,3 |
0,4 |
0,6 |
0,8 |
1,0 |
|
0,05 |
0,80 |
15 |
25 |
40 |
65 |
125 |
200 |
315 |
|
|
0,90 |
32 |
50 |
100 |
150 |
250 |
500 |
800 |
|
|
0,95 |
50 |
100 |
150 |
250 |
500 |
800 |
1000 |
|
|
0,975 |
70 |
140 |
225 |
350 |
700 |
1000 |
>1000 |
|
|
0,99 |
100 |
200 |
315 |
500 |
1000 |
>1000 |
>1000 |
|
0,10 |
0,80 |
4 |
6 |
10 |
15 |
32 |
50 |
80 |
|
|
0,90 |
8 |
15 |
25 |
40 |
80 |
125 |
200 |
|
|
0,95 |
13 |
25 |
40 |
65 |
125 |
200 |
315 |
|
|
0,975 |
18 |
36 |
57 |
90 |
180 |
285 |
462 |
|
|
0,99 |
25 |
50 |
80 |
125 |
250 |
400 |
650 |
|
0,15 |
0,80 |
3 |
3 |
5 |
8 |
15 |
25 |
40 |
|
|
0,90 |
4 |
6 |
10 |
20 |
40 |
65 |
100 |
|
|
0,95 |
6 |
10 |
20 |
32 |
65 |
100 |
150 |
|
|
0,975 |
10 |
14 |
28 |
47 |
90 |
140 |
225 |
|
|
0,99 |
13 |
20 |
40 |
65 |
125 |
200 |
315 |
|
0,20 |
0,80 |
3 |
3 |
3 |
5 |
10 |
15 |
25 |
|
|
0,90 |
3 |
4 |
6 |
10 |
20 |
40 |
65 |
|
|
0,95 |
4 |
6 |
10 |
20 |
40 |
65 |
100 |
|
|
0,975 |
6 |
10 |
14 |
28 |
56 |
90 |
140 |
|
|
0,99 |
8 |
13 |
20 |
40 |
80 |
125 |
200 |
Таблица 31
Число отказов при плане для оценки коэффициента готовности при =0,3
|
|
|
| ||||||
|
|
|
0,1 |
0,2 |
0,3 |
0,4 |
0,6 |
0,8 |
1,0 |
|
0,05 |
0,80 |
25 |
40 |
50 |
80 |
125 |
200 |
315 |
|
|
0,90 |
65 |
80 |
125 |
200 |
315 |
500 |
800 |
|
|
0,95 |
100 |
150 |
200 |
315 |
500 |
800 |
1000 |
|
|
0,975 |
136 |
217 |
271 |
434 |
678 |
1000 |
>1000 |
|
|
0,99 |
200 |
315 |
400 |
650 |
1000 |
>1000 |
>1000 |
|
0,10 |
0,80 |
6 |
10 |
15 |
20 |
40 |
65 |
100 |
|
|
0,90 |
15 |
25 |
32 |
50 |
80 |
150 |
200 |
|
|
0,95 |
25 |
40 |
50 |
80 |
150 |
250 |
400 |
|
|
0,975 |
33 |
55 |
82 |
109 |
217 |
353 |
542 |
|
|
0,99 |
50 |
80 |
100 |
150 |
250 |
400 |
650 |
|
0,15 |
0,80 |
3 |
5 |
6 |
10 |
15 |
32 |
50 |
|
|
0,90 |
8 |
10 |
15 |
25 |
40 |
65 |
100 |
|
|
0,95 |
13 |
15 |
25 |
40 |
65 |
100 |
150 |
|
|
0,975 |
17 |
27 |
33 |
55 |
82 |
174 |
271 |
|
|
0,99 |
25 |
32 |
50 |
80 |
125 |
200 |
315 |
|
0,20 |
0,80 |
3 |
4 |
4 |
6 |
10 |
20 |
25 |
|
|
0,90 |
4 |
6 |
10 |
13 |
25 |
40 |
65 |
|
|
0,95 |
6 |
10 |
15 |
20 |
40 |
65 |
100 |
|
|
0,975 |
10 |
17 |
22 |
33 |
55 |
108 |
136 |
|
|
0,99 |
13 |
20 |
32 |
40 |
80 |
125 |
200 |
Таблица 32
Число отказов при плане для оценки коэффициента готовности при =0,4
|
|
|
| ||||||
|
|
|
0,1 |
0,2 |
0,3 |
0,4 |
0,6 |
0,8 |
1,0 |
|
0,05 |
0,80 |
50 |
65 |
80 |
100 |
150 |
250 |
400 |
|
|
0,90 |
100 |
125 |
150 |
200 |
315 |
500 |
800 |
|
|
0,95 |
150 |
200 |
250 |
400 |
650 |
1000 |
>1000 |
|
|
0,975 |
271 |
353 |
434 |
542 |
813 |
1000 |
>1000 |
|
|
0,99 |
315 |
400 |
500 |
800 |
1000 |
>1000 |
>1000 |
|
0,10 |
0,80 |
13 |
15 |
20 |
25 |
40 |
65 |
100 |
|
|
0,90 |
25 |
32 |
40 |
65 |
100 |
150 |
250 |
|
|
0,95 |
40 |
50 |
80 |
100 |
150 |
250 |
400 |
|
|
0,975 |
71 |
82 |
109 |
136 |
217 |
353 |
542 |
|
|
0,99 |
100 |
125 |
150 |
200 |
315 |
500 |
800 |
|
0,15 |
0,80 |
5 |
6 |
8 |
10 |
20 |
32 |
50 |
|
|
0,90 |
13 |
15 |
20 |
25 |
50 |
80 |
100 |
|
|
0,95 |
20 |
25 |
32 |
40 |
80 |
125 |
200 |
|
|
0,975 |
27 |
33 |
44 |
55 |
109 |
173 |
271 |
|
|
0,99 |
40 |
50 |
65 |
80 |
150 |
250 |
400 |
|
0,20 |
0,80 |
3 |
4 |
5 |
6 |
13 |
20 |
32 |
|
|
0,90 |
6 |
8 |
13 |
15 |
25 |
40 |
65 |
|
|
0,95 |
10 |
13 |
20 |
25 |
40 |
65 |
100 |
|
|
0,975 |
17 |
22 |
27 |
33 |
71 |
109 |
173 |
|
|
0,99 |
25 |
32 |
40 |
50 |
80 |
150 |
200 |
Таблица 33
Число отказов при плане для оценки коэффициента готовности при =0,6
|
|
|
| ||||||
|
|
|
0,1 |
0,2 |
0,3 |
0,4 |
0,6 |
0,8 |
1,0 |
|
0,05 |
0,80 |
100 |
125 |
125 |
150 |
200 |
315 |
400 |
|
|
0,90 |
250 |
250 |
315 |
400 |
500 |
650 |
>1000 |
|
|
0,95 |
400 |
400 |
500 |
650 |
800 |
1000 |
>1000 |
|
|
0,975 |
570 |
570 |
700 |
1000 |
>1000 |
|
|
|
|
0,99 |
800 |
800 |
1000 |
>1000 |
|
|
|
|
0,10 |
0,80 |
25 |
25 |
32 |
40 |
50 |
80 |
100 |
|
|
0,90 |
65 |
65 |
80 |
100 |
125 |
200 |
250 |
|
|
0,95 |
100 |
100 |
125 |
150 |
200 |
315 |
400 |
|
|
0,975 |
140 |
140 |
180 |
225 |
285 |
460 |
570 |
|
|
0,99 |
200 |
200 |
250 |
315 |
400 |
650 |
800 |
|
0,15 |
0,80 |
10 |
13 |
15 |
20 |
25 |
40 |
50 |
|
|
0,90 |
25 |
32 |
32 |
40 |
65 |
80 |
125 |
|
|
0,95 |
40 |
50 |
50 |
65 |
100 |
150 |
200 |
|
|
0,975 |
57 |
70 |
90 |
100 |
150 |
225 |
285 |
|
|
0,99 |
80 |
100 |
125 |
150 |
200 |
315 |
400 |
|
0,20 |
0,80 |
6 |
8 |
8 |
10 |
15 |
20 |
32 |
|
|
0,90 |
15 |
15 |
20 |
25 |
40 |
50 |
80 |
|
|
0,95 |
25 |
25 |
32 |
40 |
65 |
80 |
125 |
|
|
0,975 |
36 |
36 |
47 |
57 |
90 |
100 |
180 |
|
|
0,99 |
50 |
50 |
65 |
80 |
125 |
150 |
250 |
Таблица 34
Число отказов при плане для оценки коэффициента готовности при =0,8
|
|
|
| ||||||
|
|
|
0,1 |
0,2 |
0,3 |
0,4 |
0,6 |
0,8 |
1,0 |
|
0,05 |
0,80 |
150 |
200 |
200 |
250 |
315 |
400 |
500 |
|
|
0,90 |
400 |
400 |
500 |
500 |
650 |
800 |
1000 |
|
|
0,95 |
650 |
650 |
800 |
800 |
1000 |
>1000 |
>1000 |
|
|
0,975 |
800 |
1000 |
>1000 |
|
|
|
|
|
|
0,99 |
>1000 |
|
|
|
|
|
|
|
0,10 |
0,80 |
40 |
50 |
50 |
65 |
80 |
100 |
125 |
|
|
0,90 |
100 |
100 |
125 |
150 |
150 |
250 |
315 |
|
|
0,95 |
150 |
200 |
200 |
200 |
315 |
400 |
500 |
|
|
0,975 |
225 |
285 |
285 |
285 |
285 |
570 |
700 |
|
|
0,99 |
315 |
400 |
400 |
400 |
400 |
800 |
1000 |
|
0,15 |
0,80 |
202* |
20 |
20 |
25 |
32 |
40 |
65 |
|
|
0,90 |
40 |
50 |
50 |
65 |
80 |
100 |
150 |
|
|
0,95 |
80 |
80 |
80 |
100 |
125 |
150 |
250 |
|
|
0,975 |
100 |
100 |
150 |
150 |
180 |
225 |
355 |
|
|
0,99 |
150 |
150 |
200 |
200 |
250 |
315 |
500 |
|
0,20 |
0,80 |
10 |
13 |
13 |
15 |
20 |
25 |
32 |
|
|
0,90 |
25 |
25 |
32 |
40 |
50 |
65 |
80 |
|
|
0,95 |
40 |
40 |
50 |
65 |
80 |
100 |
150 |
|
|
0,975 |
60 |
70 |
70 |
90 |
100 |
150 |
180 |
|
|
0,99 |
80 |
100 |
100 |
125 |
150 |
200 |
250 |
_______________
* Соответствует оригиналу. - Примечание .
Таблица 35
Число отказов при плане для оценки коэффициента готовности при =1,0
|
|
|
| ||||||
|
|
|
0,1 |
0,2 |
0,3 |
0,4 |
0,6 |
0,8 |
1,0 |
|
0,05 |
0,80 |
250 |
315 |
315 |
315 |
400 |
500 |
650 |
|
|
0,90 |
650 |
650 |
650 |
800 |
1000 |
1000 |
1000 |
|
|
0,95 |
>1000 |
|
|
|
|
|
|
|
|
0,975 |
>1000 |
|
|
|
|
|
|
|
|
0,99 |
>1000 |
|
|
|
|
|
|
|
0,10 |
0,80 |
65 |
65 |
80 |
80 |
100 |
125 |
150 |
|
|
0,90 |
150 |
150 |
200 |
200 |
250 |
315 |
400 |
|
|
0,95 |
250 |
250 |
315 |
315 |
400 |
500 |
650 |
|
|
0,975 |
350 |
350 |
350 |
460 |
570 |
700 |
1000 |
|
|
0,99 |
500 |
500 |
500 |
650 |
800 |
1000 |
>1000 |
|
0,15 |
0,80 |
32 |
32 |
32 |
40 |
40 |
50 |
65 |
|
|
0,90 |
65 |
80 |
80 |
80 |
100 |
125 |
150 |
|
|
0,95 |
125 |
125 |
125 |
150 |
200 |
250 |
250 |
|
|
0,975 |
180 |
180 |
180 |
225 |
225 |
285 |
350 |
|
|
0,99 |
250 |
250 |
250 |
315 |
315 |
400 |
500 |
|
0,20 |
0,80 |
15 |
20 |
20 |
20 |
25 |
32 |
40 |
|
|
0,90 |
40 |
40 |
50 |
50 |
65 |
80 |
100 |
|
|
0,95 |
65 |
65 |
80 |
80 |
100 |
125 |
150 |
|
|
0,975 |
90 |
100 |
100 |
100 |
150 |
180 |
225 |
|
|
0,99 |
125 |
150 |
150 |
150 |
200 |
250 |
315 |
ПРИЛОЖЕНИЕ 5
Рекомендуемое
ПОРЯДОК ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
ПРИ НАЛИЧИИ ОСНОВНОЙ ЭКСПЕРИМЕНТАЛЬНОЙ ИНФОРМАЦИИ
1. Оценка показателей надежности непараметрическими методами
1.1. Точечные оценки показателей надежности вычисляют при 
.
При 
используют нижние доверительные границы показателей надежности.
1.2. Последовательность вычисления оценок показателей надежности для планов типа 
:
Наработки до отказа и наработки до цензурирования (для планов, отличных от 
) выстраивают в общий вариационный ряд в порядке неубывания. Если отдельные значения наработки до отказа равны некоторым значениям наработок работоспособных изделий, то в вариационном ряду сначала указывают наработки до отказа, затем наработки до цензурирования.
Вычисляют оценку функции распределения 
; 
.
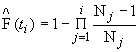где 
- количество работоспособных изделий до 
-го отказа в вариационном ряду.
Для планов , 
и 
эта формула переходит в следующую:
, 
.
Вычисляют точечные оценки показателей надежности по формулам, приведенным в табл.36.
Таблица 36
|
|
Формулы для определения | ||
|
План испытаний |
средней наработки до отказа, среднего ресурса (срока службы, срока сохраняемости, времени восстановления) |
гамма-процентной наработки, гамма-процентного ресурса (срока службы, срока сохраняемости) |
вероятности безотказности работы за наработку |
|
|
|
где
|
где
|
|
|
|
|
|
|
|
|
|
|
|
|
где
|
|
|
|
|
для изделий с возрастающей интенсивностью отказов |
|
|
,
,
,
,
, где 
;
,
, таких, что 
Примечания:
1. Среднее время восстановления оценивают для плана
2. Если выполнено одно из условий 
или 
, то 
или 
.
3. Если выполнено одно из условий 
или 
, то 
или 
.
4. Если выполнено условие 
, то 
.
При заданной доверительной вероятности * для двустороннего интервала доверительную вероятность для одностороннего интервала определяют по формуле 
. Соответственно 
.
Вычисляют интервальные оценки показателей надежности по формулам, приведенным в табл.37.
Таблица 37
Формулы для вычисления интервальных оценок показателей надежности
при неизвестном виде закона распределения
|
Показатель надежности |
Формулы для вычисления | |
|
|
нижней доверительной границы уровня |
верхней доверительной границы |
|
Средняя наработка до отказа, средний ресурс (срок службы, сохраняемости, время восстановления) |
|
|
|
Гамма-процентные показатели |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вероятность безотказной работы за наработку |
|
|
|
|
|
|
; 
; 
Примечания:
1. Оценки 
, 
являются приближенными.
2. Оценки 
, 
, 
, 
для плана 
являются приближенными.
3. Для плана
, где 
- целая часть .
4. 
; 
; 
.
5. Если выполнено одно из условий
; 
; 
или
, то 
; 
; 
или
соответственно.
6. Если выполнено одно из условий
или , то 
;
; 
или 
соответственно.
7. Если выполнено условие
, то 
; 
.
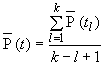1.3. Для планов и точечную оценку средней наработки на отказ вычисляют по формуле 
.
Интервальные оценки средней наработки на отказ вычисляют приближенно по формулам табл.46 и табл.47 для соответствующих планов.
1.4. Для планов испытаний типа 
точечную оценку коэффициента готовности вычисляют по формуле
,
в которой оценки средней наработки на отказ 
и среднего времени восстановления 
вычисляют по формулам п.1.3 и табл.35 соответственно.
Интервальные оценки коэффициента готовности вычисляют по формулам:
;
;
;
.
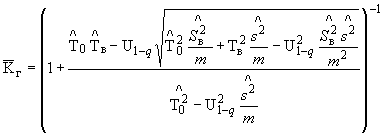2. Оценка показателей надежности параметрическими методами
2.1. Точечные оценки показателей надежности при известном законе распределения вычисляют по формулам табл.38.
2.2. Точечные оценки параметров распределений
Оценки параметра экспоненциального распределения вычисляют по формулам табл.39.
Оценка параметров распределения Вейбулла.
Для 
и плана , а также для 
и планов , и оценки параметров и вычисляют по формулам табл.40 методом линейного оценивания. Для 
при плане и 
при планах , и оценки параметров и вычисляют по формулам табл.41 методом максимального правдоподобия.
Оценка параметров нормального распределения.
Для оценки параметров и вычисляют по формулам табл.42 методом линейного оценивания.
Для 
оценки параметров и вычисляют по формулам табл.43 методом максимального правдоподобия.
Оценка параметров диффузионного распределения.
Оценки параметров диффузионного немонотонного распределения вычисляют по формулам табл.44.
Оценки параметров диффузионного монотонного распределения вычисляют по формулам табл.45.
2.3. Интервальные оценки показателей надежности
Интервальные оценки показателей надежности в случае экспоненциального распределения вычисляют по формулам табл.46.
Значения 
, 
для экспоненциального распределения вычисляют по формулам табл.47.
Интервальные оценки показателей надежности в случае распределения Вейбулла при 
вычисляют по формулам табл.48. Интервальные оценки показателей надежности в случае распределения Вейбулла для , вычисляют по формулам табл.49.
Интервальные оценки показателей надежности в случае нормального распределения вычисляют по формулам табл.51.
Интервальные оценки показателей надежности в случае диффузионного немонотонного распределения вычисляют по формулам табл.52.
Интервальные оценки показателей надежности в случае диффузионного монотонного распределения вычисляют по формулам табл.53.
2.4. Для планов испытаний и точечная и интервальная оценки средней наработки на отказ вычисляются как соответствующие оценки средней наработки до отказа по плану , при котором - число условных объектов испытаний, равное сумме числа наработок до первого отказа, наработок между отказами и наработок до цензурирования.
Таблица 38
Формулы для вычисления точечных оценок показателей надежности
при известном законе распределения
|
|
Формулы для вычисления | ||
|
Закон распределения |
средней наработки |
вероятности безотказной работы |
гамма-процентной наработки, гамма-процентного ресурса |
|
Экспоненциальный |
|
|
|
|
Вейбулла |
|
|
|
|
Нормальный |
|
|
|
|
Диффузионный монотонный |
|
|
|
|
Диффузионный немонотонный |
|
|
|
Примечания:
1. Для логарифмически нормального распределения оценки показателей надежности вычисляют по формулам для нормального распределения с заменой значений наработок их натуральными логарифмами.
2. Значения функций 
, 
, 
приведены в приложении 9.
Таблица 39
Формулы для вычисления точечной оценки параметра экспоненциального распределения
|
План испытаний |
Оценка параметра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, 
, 
, 
Таблица 40
Формулы для вычисления точечных оценок параметров распределения Вейбулла (
)
|
План испытаний |
Формулы для определения | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примечания:
1. Коэффициенты 
и 
- для планов , и определяют по табл.62 приложения 9 при 
15; для плана при 6 - по табл.61 приложения 9.
2. Наработки до отказа и наработки до цензурирования выстраивают в вариационный ряд в порядке неубывания наработок.
Таблица 41
Формулы для вычисления точечных оценок параметров распределения Вейбулла ()
|
План испытаний |
Формулы для определения | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*_______________
* Формула соответствует оригиналу. - Примечание .
Примечание. Порядок решения уравнений относительно параметра приведен в приложении 7.
Таблица 42
Формулы для вычисления точечных оценок параметров нормального распределения ()
|
План испытаний |
Выражение для оценки параметров | |
|
|
|
|
|
|
|
|
|
|
|
|
Примечания:
1. Коэффициенты 
и 
приведены в табл.64 приложения 9.
2. Наработки до отказа выстраивают в вариационный ряд в порядке неубывания наработок.
Таблица 43
Формулы для вычисления точечных оценок параметров нормального распределения ()
|
План испытаний |
Расчетные формулы |
|
|
|
|
|
|
|
|
|
; 
Примечания:
1. Порядок решения уравнений относительно и для планов испытаний , , приведен в приложении 7.
2. Значения 
приведены в табл.67 приложения 9.
Таблица 44
Формулы для вычисления точечных оценок параметров диффузионного немонотонного распределения
|
План испытаний |
Расчетные формулы |
|
|
|
|
|
|
; 
; 
; 
Таблица 45
Формулы для вычисления точечных оценок параметров диффузионного монотонного распределения
|
План испытаний |
Расчетные формулы | |
|
|
| |
|
|
| |
|
|
| |
|
|
|
|
Примечание. Оценки параметров и определяют методом последовательных приближений.
Таблица 46
Формулы для вычисления интервальных оценок показателей надежности
для экспоненциального закона распределения
|
Наименование показателя надежности |
Формулы для вычисления доверительных границ уровня | |
|
|
нижней |
верхней |
|
Средняя наработка до отказа (на отказ) |
|
|
|
Гамма-процентный ресурс (срок службы, срок сохраняемости) |
|
|
|
Вероятность безотказной работы за наработку |
|
|
|
Интенсивность отказов |
|
|
Таблица 47
Формулы для вычисления доверительных границ параметра экспоненциального распределения
|
План испытаний |
Формулы для вычисления доверительных границ уровня | |
|
|
нижней |
верхней |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; 
; 
; 
; 
, 
, 
, 
,
Примечания:
1. Оценки для плана являются приближенными.
2. Значения 
приведены в табл.68 приложения 9.
3. Значения 
приведены в табл.66 приложения 9.
Таблица 48
Формулы для вычисления интервальных оценок показателей надежности для распределения Вейбулла ()
|
Показатель надежности |
Формулы для вычисления доверительных границ уровня | |
|
|
нижней |
верхней |
|
Средняя наработка до отказа |
|
|
|
Средний ресурс (срок службы, срок сохраняемости, время восстановления) |
|
|
|
Гамма-процентная наработка до отказа |
|
|
|
Гамма-процентный ресурс (срок службы, срок сохраняемости) |
|
|
|
Вероятность безотказной работы за наработку |
|
- |
Примечания:
1. Значения функций 
, 
приведены в табл.65 и табл.69-71 приложения 9.
2. Для плана значения и находят для 
.
3. Значения 
находят интерполяцией между значениями 
и 
. В противном случае переходят к вычислениям по формулам табл.49.
4. Если за время испытаний отказы не зафиксированы, то нижнюю доверительную границу средней наработки до отказа 
вычисляют по формуле 
, нижнюю доверительную границу гамма-процентной наработки до отказа 
вычисляют по формуле
.
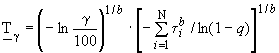Параметр формы распределения при этом принимают известным.
Таблица 49
Формулы для вычисления интервальных оценок показателей надежности
для распределения Вейбулла (
)
|
Показатель надежности |
Формулы для вычисления доверительных границ уровня | |
|
|
нижней |
верхней |
|
Средняя наработка до отказа |
|
|
|
Средний ресурс (срок службы, срок сохраняемости, время восстановления) |
|
|
|
Гамма-процентная наработка до отказа |
|
|
|
Гамма-процентный ресурс (срок службы, срок сохраняемости) |
|
|
|
Вероятность безотказной работы за наработку |
|
|
Примечания:
1. Значения 
и 
определяют по графикам, изображенным на черт.1-9 для доверительной вероятности 
=0,80; 0,90; 0,95, соответствующей двустороннему доверительному интервалу.
2. На оси абсцисс соответствующего графика откладывают значение 
и восстанавливают перпендикуляр до пересечения с кривыми, соответствующими объему наблюдений выборки. Ординаты точки пересечения, отсчитанные по соответствующей шкале , указывают значения (на нижней половине шкалы) и (на верхней половине шкалы).
Значение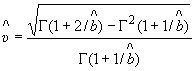 
.
3. Формулы для вычисления 
, 
приведены в табл.50.
4. Оценки являются приближенными.
Таблица 50
Формулы для вычисления приближенных значений дисперсий и 
|
Обозначение дисперсии и вспомогатель- |
Формулы для вычисления |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примечания:
1. В формулы подставляют оценки параметров и , вычисленные согласно п.2.2 приложения 5.
2. Для плана 
; 
.
3. Для плана 
.
Таблица 51
Формулы для вычисления интервальных оценок показателей надежности
для нормального распределения
|
Показатель надежности |
Формулы для вычисления доверительных границ уровня | |
|
|
нижней |
верхней |
|
Средняя наработка до отказа (средний ресурс, срок службы, срок сохраняемости, время восстановления) |
|
|
|
Гамма-процентная наработка до отказа, гамма-процентный ресурс (срок службы, срок сохраняемости) |
|
|
|
Вероятность безотказной работы за наработку |
|
|
, 
,
, 
,
Примечания:
1. Для плана 
.
2. Для планов , , оценки являются приближенными.
3. Значения 
приведены в табл.73 приложения 9.
4. Значения 
приведены в табл.72 приложения 9.
5. Для плана 
.
6. Если за время испытаний отказов не зафиксировано, то нижние доверительные границы средней наработки до отказа 
и гамма-процентной наработки до отказа 
вычисляют приближенно по формулам:
;
.
Значения 
и 
определяют по табл.76 приложения 9.
Коэффициент вариации при этом полагается известным.
Таблица 52
Формулы для вычисления интервальных оценок показателей надежности
для диффузионного немонотонного распределения
|
Показатель надежности |
Формулы для вычисления доверительных границ уровня | |
|
|
нижней |
верхней |
|
Средняя наработка до отказа |
|
|
|
Средний ресурс (срок службы, срок сохраняемости, время восстановления) |
|
|
|
Гамма-процентная наработка до отказа |
|
|
|
Гамма-процентный ресурс (срок службы, срок сохраняемости) |
|
|
|
Вероятность безотказной работы за наработку |
|
|
Примечание. Значения 
вычисляют по формулам табл.54.
Таблица 53
Формулы для вычисления интервальных оценок показателей надежности
для диффузионного монотонного распределения
|
Показатель надежности |
Формулы для вычисления доверительных границ уровня | |
|
|
нижней |
верхней |
|
Средняя наработка до отказа |
|
|
|
Средний ресурс (срок службы, срок сохраняемости, время восстановления) |
|
|
|
Гамма-процентная наработка до отказа |
|
|
|
Гамма-процентный ресурс (срок службы, срок сохраняемости) |
|
|
|
Вероятность безотказной работы за наработку |
|
|
Таблица 54
Формулы для вычисления доверительных границ параметров диффузионных распределений
|
План испы- |
НДГ уровня |
ВДГ уровня |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценка доверительных границ средней наработки до отказа для =0,80
Цифры на кривых указывают объем выборки
Черт.1
Оценка доверительных границ средней наработки до отказа для =0,90
Цифры на кривых указывают объем выборки
Черт.2
Оценка доверительных границ средней наработки до отказа для =0,95
Цифры на кривых указывают объем выборки
Черт.3
Оценка доверительных границ 80% наработки до отказа для =0,80
Цифры на кривых указывают объем выборки
Черт.4
Оценка доверительных границ 80% наработки до отказа для =0,90
Цифры на кривых указывают объем выборки
Черт.5
Оценка дoвepитeльныx границ 80% наработки до отказа =0,95
Цифры на кривых указывают объем выборки
Черт.6
Оценка доверительных границ 90% наработки до отказа для =0,80
Цифры на кривых указывают объем выборки
Черт.7
Оценка доверительных границ 90% наработки до отказа для =0,90
Цифры на кривых указывают объем выборки
Черт.8
Оценка дoвepитeльныx границ 90% наработки до отказа =0,95
Цифры на кривых указывают объем выборки
Черт.9
ПРИЛОЖЕНИЕ 6
Рекомендуемое
ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ ПРИ НАЛИЧИИ
ОСНОВНОЙ И ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИИ ОБ ОБЪЕКТЕ
1. Параметрические методы оценки
1.1. Оценка показателей надежности при ТС-1-ТС-4
1.1.1. Точечные оценки показателей надежности вычисляют в два этапа:
оценка параметров законов распределения;
оценка показателей надежности по вычисленным оценкам параметров закона распределения.
1.1.2. Формулы для определения точечных оценок параметров распределений для ТС-1-ТС-4 приведены в табл.55, вспомогательных величин - в табл.56, дисперсии оценок параметров - в табл.55.
Формулы табл.55, 57 приведены для плана испытаний . Для планов испытаний наработки работоспособных объектов 
имеют следующий вид:
|
|
при плане испытаний |
Оценки параметров нормального закона распределения определяют в соответствии с табл.55 методом последовательных приближений.
Таблица 55
Формулы для определения точечных оценок параметров однопараметрических законов распределения
и двухпараметрических (при одном известном параметре)
|
Закон распределения |
Формулы для определения |
|
Экспоненциальный |
|
|
Вейбулла |
|
|
Нормальный |
|
- известны)
- известны)
Примечания:
1. 
.
2. 
, 
- нормированные и центрированные плотность и функция распределения нормального закона соответственно.
3. Значения 
, 
, 
приведены в табл.56.
Таблица 56
Формулы для определения вспомогательных величин , , (>1)
|
ТС |
Формулы для определения | ||
|
|
|
|
|
|
ТС-1 |
1 |
1 |
1 |
|
ТС-2 |
|
|
1 |
|
ТС-3 |
|
|
|
|
_______________ | |||
|
ТС-4 |
1 |
1 |
|
Примечания:
1. 
- оценка параметра 
, полученная по -й группе дополнительных данных (>1); 
- оценка параметра 
, полученная по основной информации. Для экспоненциального, нормального и логарифмически нормального законов распределения 
.
2. 
.
3. Для нормального и логарифмически нормального законов распределений 
.
Таблица 57
Формулы для вычисления дисперсий оценок
|
Закон распределения |
Формулы для определения |
|
Экспоненциальный |
|
|
Вейбулла |
|
|
Нормальный |
|
Примечание. Значения , , находят по табл.56.
1.1.3. Точечные оценки показателей надежности по вычисленным точечным оценкам параметров распределений вычисляют по формулам табл.38 приложения 5.
1.1.4. Интервальные оценки показателей надежности в случае ТС-1-ТС-3 вычисляют по приближенным формулам:
,
.
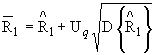1.1.5. Дисперсии оценок показателей надежности 
вычисляют по формуле:
,
где 
- параметр закона распределения.
1.1.6. Интервальные оценки показателей надежности при ТС-1 вычисляют подстановкой в выражение показателя надежности значений верхней и нижней границ соответствующего параметра.
Если 
, 
.
Если 
, 
.
Здесь 
, 
- односторонние доверительные границы параметра , соответствующие доверительной вероятности 
, полученные по основной информации в соответствии с приложением 5;
, 
- односторонние доверительные границы, соответствующие доверительной вероятности и полученные в соответствии с приложением 5 по всей совокупности дополнительной информации (см. ТС-1).
1.2. Оценка показателей надежности при ТС-4.
1.2.1. Точечные и интервальные оценки показателей надежности определяют в два этапа:
вычисляют точечные и интервальные оценки вероятности безотказной работы;
вычисляют точечные и интервальные оценки показателей надежности на основе известных оценок вероятности безотказной работы.
1.2.2. В качестве исходной информации для определения оценок показателей надежности используются исходные данные, перечисленные в п.4.3, или точечные оценки и нижние доверительные границы вероятности безотказной работы 
, 
, 
, полученные по основной и дополнительной информации соответственно.
В последнем случае необходимо провести предварительную обработку исходных данных в соответствии с РД 50-476.
1.2.3. Точечная оценка вероятности безотказной работы определяется по формуле
,
где
;
;
;
.
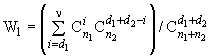2. Непараметрические методы оценки
2.1. В качестве исходной информации используют точечные оценки 
показателя надежности и их дисперсии 
, полученные по основной и дополнительной информации соответственно.
2.2. Точечную оценку показателя надежности 
и ее дисперсию 
вычисляют по формулам:
,
.
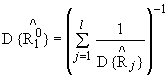2.1. Интервальные оценки показателя надежности 
определяют по формулам п.1.1.4.
ПРИЛОЖЕНИЕ 7
Рекомендуемое
ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ
МЕТОДОМ ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
1. Оценка параметров распределения Вейбулла методом последовательных приближений.
Оценку параметров и вычисляют в соответствии с формулами табл.41 решением уравнения относительно и последовательности пп.1.1-1.7:
1.1. Вычисляют коэффициент 
: 
,
где 
1.2. Вычисляют начальное приближение 
.
1.3. Вычисляют следующее приближение 
(
=1, 2)
,
где 
1.4. Процесс нахождения приближений прекращают при
.
1.5. Значения выбирают из ряда 0,0001, 0,001; 0,01; 0,1. При этом чем точнее результаты испытаний, тем меньше значение .
При решении уравнения на ЭВМ значение должно быть не менее 0,01.
1.6. Значение , отвечающее неравенству 1.4, принимают в качестве оценки параметра 
.
1.7. Найденную оценку подставляют в выражение для параметра .
2. Оценка параметров нормального распределения методом последовательных приближений.
Уравнение табл.43 решают в последовательности пп.2.1-2.5.
2.1. Вычисляют вспомогательные коэффициенты согласно табл.58.
Таблица 58
|
Коэффициент |
План испытаний |
Расчетное выражение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.2. Вычисляют начальные приближения 
и 
для оценок и :
;
.
2.3. Вычисляют коэффициенты для планов или
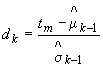
2.4. Вычисляют коэффициенты для плана :
;
;
*;
_______________
* Формула соответствует оригиналу. - Примечание .
;
.
2.5. Вычисляют последующие приближения приближения 
и 
для оценок и :
.
За оценки параметров и принимают значения и , для которых соблюдаются условия:
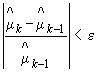и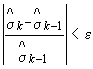 
,
где выбирают из ряда 0,001, 0,01; 0,05; 0,1.
3. Оценка параметра нормального распределения 
Уравнения табл.55 решают в последовательности пп.3.1-3.3.
3.1. Вычисляют коэффициенты:
;
;
;
;
;
;
, 
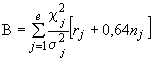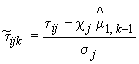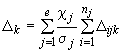3.2. Вычисляют начальное приближение
.
Вычисляют последующие приближения:
.
3.3. За оценку параметра 
принимают значение 
, для которого соблюдается условие
,
где выбирают из ряда 0,001; 0,01; 0,05; 0,1.
4. Значения 
приведены в табл.74 приложения 9.
ПРИЛОЖЕНИЕ 8
Рекомендуемое
ОЦЕНКА ВЕРОЯТНОСТИ БЕЗОТКАЗНОЙ РАБОТЫ
В СЛУЧАЕ БИНОМИАЛЬНЫХ ИСПЫТАНИЙ
1. Точечную оценку вероятности безотказной работы 
за наработку (время) вычисляют по формуле:
.
2. Интервальные оценки вероятности безотказной работы за наработку .
2.1. Нижнюю доверительную границу вероятности безотказной работы 
за наработку уровня вычисляют по приближенным формулам:
, 
;
, 
.
Значения 
определяют по табл.75 приложения 9.
Значения 
определяют по табл.68 приложения 9.
2.2. Верхнюю доверительную границу вероятности безотказной работы 
за наработку уровня вычисляют по приближенным формулам:
, ;
, .
ПРИЛОЖЕНИЕ 9
Справочное
ТАБЛИЦЫ ДЛЯ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
Таблица 59
|
|
|
|
|
0,00 |
1,0000 |
1,0000 |
|
01 |
1,0101 |
0,9900 |
|
02 |
1,0202 |
0,9802 |
|
03 |
1,0305 |
0,9704 |
|
04 |
1,0408 |
0,9608 |
|
0,05 |
1,0513 |
0,9512 |
|
06 |
1,0618 |
0,9418 |
|
07 |
1,0725 |
09324 |
|
08 |
1,0833 |
0,9231 |
|
09 |
1,0942 |
0,9139 |
|
0,10 |
1,1052 |
0,9048 |
|
11 |
1,1163 |
0,8958 |
|
12 |
1,1275 |
0,8869 |
|
13 |
1,1388 |
0,8781 |
|
14 |
1,1503 |
0,8694 |
|
0,15 |
1,1618 |
0,8607 |
|
16 |
1,1835 |
0,8521 |
|
17 |
1,1853 |
0,8437 |
|
18 |
1,1972 |
0,8353 |
|
19 |
1,2092 |
0,8270 |
|
0,20 |
1,2214 |
0,8187 |
|
21 |
1,2337 |
0,8106 |
|
22 |
1,2461 |
0,8025 |
|
23 |
1,2586 |
0,7945 |
|
24 |
1,2712 |
0,7866 |
|
0,25 |
1,2840 |
0,7788 |
|
26 |
1,2969 |
0,7711 |
|
27 |
1,3100 |
0,7634 |
|
28 |
1,3231 |
0,7558 |
|
29 |
1,3364 |
0,7483 |
|
0,30 |
1,3499 |
0,7408 |
|
31 |
1,3634 |
0,7334 |
|
32 |
1,3771 |
0,7261 |
|
33 |
1,3910 |
0,7189 |
|
34 |
1,4049 |
0,7118 |
|
0,35 |
1,4191 |
0,7047 |
|
36 |
1,4333 |
0,6977 |
|
37 |
1,4477 |
0,6907 |
|
38 |
1,4623 |
0,6839 |
|
39 |
1,4770 |
0,6771 |
|
0,40 |
1,4918 |
0,6703 |
|
41 |
1,5068 |
0,6637 |
|
42 |
1,5220 |
0,6570 |
|
43 |
1,5373 |
0,6505 |
|
44 |
1,5227 |
0,6440 |
|
0,45 |
1,5683 |
0,6376 |
|
46 |
1,5841 |
0,6313 |
|
47 |
1,6000 |
0,6250 |
|
48 |
1,6161 |
0,6188 |
|
49 |
1,6323 |
0,6126 |
|
0,50 |
1,6487 |
0,6065 |
|
51 |
1,6658 |
0,6005 |
|
52 |
1,6820 |
0,5945 |
|
53 |
1,6989 |
0,5886 |
|
54 |
1,7160 |
0,5827 |
|
0,55 |
1,7333 |
0,5769 |
|
56 |
1,7507 |
0,5712 |
|
57 |
1,7683 |
0,5655 |
|
58 |
1,7860 |
0,5599 |
|
59 |
1,8040 |
0,5543 |
|
0,60 |
1,8221 |
0,5488 |
|
61 |
1,8404 |
0,5434 |
|
62 |
1,8589 |
0,5379 |
|
63 |
1,8776 |
0,5326 |
|
64 |
1,8965 |
0,5273 |
|
0,65 |
1,9155 |
0,5220 |
|
66 |
1,9348 |
0,5169 |
|
67 |
1,9542 |
0,5117 |
|
68 |
1,9739 |
0,5066 |
|
69 |
1,9937 |
0,5016 |
|
0,70 |
2,0138 |
0,4966 |
|
71 |
2,0340 |
0,4916 |
|
72 |
2,0544 |
0,4868 |
|
73 |
2,0751 |
0,4819 |
|
74 |
2,0959 |
0,4771 |
|
0,75 |
2,1170 |
0,4724 |
|
76 |
2,1383 |
0,4677 |
|
77 |
2,1598 |
0,4630 |
|
78 |
2,1815 |
0,4584 |
|
79 |
2,2034 |
0,4538 |
|
0,80 |
2,2255 |
0,4493 |
|
81 |
2,2479 |
0,4449 |
|
82 |
2,2705 |
0,4404 |
|
83 |
2,2933 |
0,4360 |
|
84 |
2,3164 |
0,4317 |
|
0,85 |
2,3396 |
0,4274 |
|
86 |
2,3632 |
0,4232 |
|
87 |
2,3869 |
0,4190 |
|
88 |
2,4109 |
0,4148 |
|
89 |
2,4351 |
0,4107 |
|
0,90 |
2,4596 |
0,4066 |
|
91 |
2,4843 |
0,4025 |
|
92 |
2,5093 |
0,3985 |
|
93 |
2,5345 |
0,3946 |
|
94 |
2,5600 |
0,3906 |
|
0,95 |
2,5857 |
0,3867 |
|
96 |
2,6117 |
0,3829 |
|
97 |
2,6379 |
0,3791 |
|
98 |
2,6645 |
0,3753 |
|
99 |
2,6912 |
0,3716 |
|
1,00 |
2,7183 |
0,3679 |
|
01 |
2,7456 |
0,3642 |
|
02 |
2,7732 |
0,3606 |
|
03 |
2,8011 |
0,3570 |
|
04 |
2,8292 |
0,3535 |
|
1,05 |
2,8577 |
0,3499 |
|
06 |
2,8864 |
0,3465 |
|
07 |
2,9154 |
0,3430 |
|
08 |
2,9447 |
0,3396 |
|
09 |
2,9743 |
0,3362 |
|
1,10 |
3,0042 |
0,3329 |
|
11 |
3,0344 |
0,3296 |
|
12 |
3,0649 |
0,3263 |
|
13 |
3,0957 |
0,3230 |
|
14 |
3,1268 |
0,3198 |
|
1,15 |
3,1582 |
0,3166 |
|
16 |
3,1899 |
0,3135 |
|
17 |
3,2220 |
0,3140 |
|
18 |
3,2544 |
0,3073 |
|
19 |
3,2871 |
0,3042 |
|
1,20 |
3,3201 |
0,3012 |
|
21 |
3,3535 |
0,2982 |
|
22 |
3,3872 |
0,2952 |
|
23 |
3,4212 |
0,2923 |
|
24 |
3,4556 |
0,2894 |
|
1,25 |
3,4903 |
0,2865 |
|
26 |
3,5254 |
0,2837 |
|
27 |
3,5609 |
0,2808 |
|
28 |
3,6328 |
0,2753 |
|
1,30 |
3,6693 |
0,2725 |
|
31 |
3,7062 |
0,2698 |
|
32 |
3,7434 |
0,2671 |
|
33 |
3,7810 |
0,2645 |
|
34 |
3,8190 |
0,2618 |
|
1,35 |
3,8574 |
0,2592 |
|
36 |
3,8962 |
0,2567 |
|
37 |
3,9354 |
0,2541 |
|
38 |
3,9749 |
0,2516 |
|
39 |
4,0149 |
02491 |
|
1,40 |
4,0552 |
0,2466 |
|
41 |
4,0960 |
0,2441 |
|
42 |
4,1371 |
0,2417 |
|
43 |
4,1787 |
0,2393 |
|
44 |
4,2207 |
0,2369 |
|
1,45 |
4,2631 |
0,2346 |
|
46 |
4,3060 |
0,2322 |
|
47 |
4,3492 |
0,2299 |
|
48 |
4,3929 |
0,2276 |
|
49 |
4,4371 |
0,2254 |
|
1,50 |
4,4817 |
0,2231 |
|
51 |
4,5267 |
0,2209 |
|
52 |
4,5722 |
0,2187 |
|
53 |
4,6182 |
0,2165 |
|
54 |
4,6646 |
0,2144 |
|
1,55 |
4,7115 |
0,2122 |
|
56 |
4,7588 |
0,2101 |
|
57 |
4,8066 |
0,2080 |
|
58 |
4,8550 |
0,2060 |
|
59 |
4,9037 |
0,2039 |
|
1,60 |
4,9530 |
0,2019 |
|
65 |
5,2070 |
0,1920 |
|
70 |
5,4739 |
0,1827 |
|
75 |
5,7546 |
0,1738 |
|
80 |
6,0496 |
0,1653 |
|
1,85 |
6,3598 |
0,1572 |
|
90 |
6,6859 |
0,1496 |
|
95 |
7,0287 |
0,1423 |
|
00 |
7,3891 |
0,1353 |
|
05 |
7,7679 |
0,1287 |
|
2,10 |
8,1662 |
0,1226 |
|
15 |
8,5849 |
0,1165 |
|
20 |
9,0250 |
0,1108 |
|
25 |
9,4877 |
0,1054 |
|
30 |
9,9742 |
0,1003 |
|
2,35 |
10,4860 |
0,0954 |
|
40 |
11,0230 |
0,0907 |
|
45 |
11,5880 |
0,0863 |
|
50 |
12,1820 |
0,0821 |
|
55 |
12,8070 |
0,0781 |
|
2,60 |
13,4640 |
0,0743 |
|
65 |
14,1540 |
0,0706 |
|
70 |
14,8800 |
0,0672 |
|
75 |
15,6430 |
0,0639 |
|
80 |
16,4450 |
0,0608 |
|
2,85 |
17,2880 |
0,0573 |
|
90 |
18,1740 |
0,0550 |
|
95 |
19,1060 |
0,0523 |
|
00 |
20,0860 |
0,0498 |
|
05 |
21,1150 |
0,0474 |
|
3,10 |
22,1980 |
0,0451 |
|
15 |
23,3360 |
0,0429 |
|
20 |
24,5330 |
0,0408 |
|
25 |
25,7800 |
0,0388 |
|
30 |
27,1130 |
0,0369 |
|
3,35 |
28,5030 |
0,0351 |
|
40 |
29,9640 |
0,0334 |
|
45 |
31,5000 |
0,0318 |
|
50 |
33,1150 |
0,0302 |
|
55 |
34,8130 |
0,0287 |
|
3,60 |
36,5980 |
0,0273 |
|
65 |
38,4750 |
0,0260 |
|
70 |
40,4470 |
0,0247 |
|
75 |
42,5210 |
0,0235 |
|
80 |
44,7010 |
0,0224 |
|
3,85 |
46,9930 |
0,0213 |
|
3,90 |
49,4020 |
0,0202 |
|
3,95 |
51,9350 |
0,0192 |
|
4,00 |
54,5980 |
0,0183 |
|
4,50 |
90,017 |
0,0111 |
|
5,0 |
148,41 |
0,006740 |
|
5,5 |
244,69 |
0,004090 |
|
6,0 |
403,43 |
0,002479 |
|
6,5 |
665,14 |
0,001503 |
|
7,0 |
1096,60 |
0,000912 |
|
7,5 |
1808,00 |
0,000553 |
|
8,0 |
2981,00 |
0,000335 |
|
8,5 |
4914,80 |
0,000203 |
|
9,0 |
8103,10 |
0,000123 |
|
9,5 |
13360,00 |
0,000075 |
|
10,0 |
22026,00 |
0,000045 |
Примечание. Для <0,01
;
или 
.
Таблица 60
Функция нормального распределения
|
|
0, |
1, |
2, |
3, |
|
,00 |
0,500 |
0,841 |
0,9777 |
0,9 |
|
,05 |
520 |
853 |
789 |
886 |
|
,10 |
540 |
864 |
821 |
0,9 |
|
,15 |
560 |
875 |
842 |
184 |
|
,20 |
573 |
885 |
861 |
313 |
|
,25 |
599 |
894 |
878 |
423 |
|
,30 |
618 |
0,9032 |
893 |
517 |
|
,35 |
637 |
115 |
906 |
596 |
|
,40 |
655 |
192 |
0,9 |
663 |
|
,45 |
674 |
265 |
286 |
720 |
|
,50 |
692 |
332 |
379 |
767 |
|
,55 |
709 |
394 |
461 |
807 |
|
,60 |
726 |
452 |
534 |
841 |
|
,65 |
742 |
505 |
589 |
860 |
|
,70 |
758 |
554 |
653 |
892 |
|
,75 |
773 |
599 |
702 |
912 |
|
,80 |
788 |
641 |
745 |
0,9 |
|
,85 |
802 |
678 |
781 |
409 |
|
,90 |
816 |
713 |
813 |
519 |
|
,95 |
829 |
744 |
841 |
609 |
865
032
Примечание. Символ 
означает 
, соответственно. Например, 0,9
277=0,9999277.
Таблица 61
Значения гамма-функции
|
|
|
|
1,00 |
1,00000 |
|
01 |
0,99433 |
|
02 |
0,98884 |
|
03 |
0,98355 |
|
04 |
0,97814 |
|
1,05 |
0,97350 |
|
06 |
0,96874 |
|
07 |
0,96415 |
|
08 |
0,95973 |
|
09 |
0,95546 |
|
1,10 |
0,95135 |
|
11 |
0,94740 |
|
12 |
0,94359 |
|
13 |
0,93993 |
|
14 |
0,93642 |
|
1,15 |
0,93304 |
|
16 |
0,92980 |
|
17 |
0,92670 |
|
18 |
0,92373 |
|
19 |
0,92089 |
|
1,20 |
0,91817 |
|
21 |
0,91558 |
|
22 |
0,91311 |
|
23 |
0,91075 |
|
24 |
0,90852 |
|
25 |
0,90640 |
|
1,26 |
0,90440 |
|
27 |
0,90250 |
|
28 |
0,90072 |
|
29 |
0,89904 |
|
1,30 |
0,89747 |
|
31 |
0,89600 |
|
32 |
0,89464 |
|
33 |
0,89338 |
|
34 |
0,89222 |
|
1,35 |
0,89115 |
|
36 |
0,89018 |
|
37 |
0,88931 |
|
1,38 |
0,88854 |
|
39 |
0,88785 |
|
1,40 |
0,88726 |
|
41 |
0,88676 |
|
42 |
0,88636 |
|
43 |
0,88604 |
|
44 |
0,88581 |
|
1,45 |
0,88566 |
|
46 |
0,88560 |
|
47 |
0,88563 |
|
48 |
0,88575 |
|
49 |
0,88595 |
|
50 |
0,88623 |
|
1,51 |
0,88659 |
|
52 |
0,88704 |
|
53 |
0,88757 |
|
54 |
0,88818 |
|
1,55 |
0,88887 |
|
56 |
0,88964 |
|
57 |
0,89049 |
|
58 |
0,89142 |
|
59 |
0,89243 |
|
1,60 |
0,89352 |
|
61 |
0,89468 |
|
62 |
0,89592 |
|
63 |
0,89724 |
|
64 |
0,89864 |
|
1,65 |
0,90012 |
|
66 |
0,90167 |
|
67 |
0,90330 |
|
68 |
0,90500 |
|
69 |
0,90678 |
|
1,70 |
0,90864 |
|
71 |
0,91057 |
|
72 |
0,91258 |
|
73 |
0,91467 |
|
74 |
0,91683 |
|
75 |
0,91906 |
|
1,75 |
0,91906 |
|
76 |
0,92137 |
|
77 |
0,92376 |
|
78 |
0,92623 |
|
79 |
0,92877 |
|
1,80 |
0,93138 |
|
81 |
0,93408 |
|
82 |
0,93685 |
|
83 |
0,94261 |
|
84 |
0,93969 |
|
1,85 |
0,94561 |
|
86 |
0,94869 |
|
87 |
0,95184 |
|
88 |
0,95507 |
|
89 |
0,95838 |
|
1,90 |
0,96177 |
|
91 |
0,96523 |
|
92 |
0,96877 |
|
93 |
0,97240 |
|
94 |
0,97610 |
|
1,95 |
0,97988 |
|
96 |
0,98374 |
|
97 |
0,98768 |
|
98 |
0,99171 |
|
99 |
0,99581 |
|
2,00 |
1,00000 |
Таблица 62
Коэффициенты для нахождения линейных оценок параметров
закона распределения Вейбулла (
)
|
|
|
Чередование отказов |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
2 |
2 |
0 |
1 |
0,110731 |
-0,421383 |
0,037574 |
0,415839 |
|
|
|
0 |
2 |
0,889269 |
0,421383 |
|
|
|
3 |
3 |
0 |
1 |
0,081063 |
-0,278686 |
|
|
|
|
|
0 |
2 |
0,250001 |
-0,190239 |
-0,018421 |
0,256346 |
|
|
|
0 |
3 |
0,667936 |
0,468904 |
|
|
|
3 |
2 |
0 |
1 |
-0,168001 |
-0,452110 |
|
|
|
|
|
0,1 |
2 |
1,168001 |
0,452110 |
|
|
|
3 |
2 |
0,1 |
1 |
0,069301 |
-0,382326 |
0,142111 |
0,369957 |
|
|
|
0 |
2 |
0,930699 |
0,382326 |
|
|
|
4 |
4 |
0 |
1 |
0,064336 |
-0,203052 |
|
|
|
|
|
0 |
2 |
0,147340 |
-0,182749 |
|
|
|
|
|
0 |
3 |
0,261510 |
-0,070109 |
-0,028312 |
0,183861 |
|
|
|
0 |
4 |
0,526813 |
0,455910 |
|
|
|
4 |
3 |
0 |
1 |
-0,044975 |
-0,297651 |
|
|
|
|
|
0 |
2 |
0,088057 |
-0,234054 |
0,084775 |
0,281729 |
|
|
|
0,1 |
3 |
0,956918 |
0,531705 |
|
|
|
4 |
2 |
0 |
1 |
-0,346974 |
-0,465455 |
0,413508 |
0,464387 |
|
|
|
0,2 |
2 |
1,346974 |
0,465455 |
|
|
|
4 |
3 |
0 |
1 |
-0,012081 |
-0,264079 |
|
|
|
|
|
0,1 |
2 |
0,299303 |
-0,164524 |
0,052960 |
0,247855 |
|
|
|
0 |
3 |
0,712777 |
0,428603 |
|
|
|
4 |
3 |
0,1 |
1 |
0,074005 |
-0,266086 |
|
|
|
|
|
0 |
2 |
0,212711 |
-0,167706 |
0,020593 |
0,230218 |
|
|
|
0 |
3 |
0,713284 |
0,433792 |
|
|
|
4 |
2 |
0,1 |
1 |
-0,181349 |
-0,421383 |
0,325811 |
0,415839 |
|
|
|
0,1 |
2 |
1,181349 |
0,421383 |
|
|
|
4 |
2 |
0,2 |
1 |
0,045963 |
-0,357407 |
0,200074 |
0,339370 |
|
|
|
0 |
2 |
0,954037 |
0,357407 |
|
|
|
5 |
5 |
0 |
1 |
0,052975 |
-0,158131 |
|
|
|
|
|
0 |
2 |
0,103531 |
-0,155707 |
|
|
|
|
|
0 |
3 |
0,163808 |
-0,111820 |
-0,029135 |
0,142842 |
|
|
|
0 |
4 |
0,246092 |
-0,005600 |
|
|
|
|
|
0 |
5 |
0,433593 |
0,431259 |
|
|
|
5 |
4 |
0 |
1 |
-0,006983 |
-0,217766 |
|
|
|
|
|
0 |
2 |
0,059652 |
-0,199351 |
0,030763 |
0,202418 |
|
|
|
0 |
3 |
0,156664 |
-0,118927 |
|
|
|
|
|
0,1 |
4 |
0,790668 |
0,536044 |
|
|
|
5 |
3 |
0 |
1 |
-0,137958 |
-0,306562 |
|
|
|
|
|
0 |
2 |
-0,025510 |
-0,257087 |
0,166128 |
0,294191 |
|
|
|
0,2 |
3 |
1,163468 |
0,563650 |
|
|
|
5 |
2 |
0 |
1 |
-0,481434 |
-0,472962 |
0,533791 |
0,472308 |
|
|
|
0,3 |
2 |
0,481434 |
-0,472962 |
|
|
|
5 |
4 |
0 |
1 |
0,006272 |
-0,199827 |
|
|
|
|
|
0 |
2 |
0,071450 |
-0,185334 |
0,018408 |
0,184873 |
|
|
|
0,1 |
3 |
0,358861 |
-0,031785 |
|
|
|
|
|
0 |
4 |
0,563417 |
0,416946 |
|
|
|
5 |
4 |
0 |
1 |
0,019987 |
-0,187558 |
|
|
|
|
|
0,1 |
2 |
0,177372 |
-0,175573 |
0,005419 |
0,172571 |
|
|
|
0 |
3 |
0,288100 |
-0,066223 |
|
|
|
|
|
0 |
4 |
0,574540 |
0,429354 |
|
|
|
5 |
3 |
0 |
1 |
-0,112966 |
-0,286914 |
|
|
|
|
|
0,1 |
2 |
0,136485 |
- 0,206143 |
0,141366 |
0,274164 |
|
|
|
0,1 |
3 |
0,976501 |
0,493057 |
|
|
|
5 |
4 |
0,1 |
1 |
0,065888 |
-0,200080 |
|
|
|
|
|
0 |
2 |
0,126234 |
-0,166466 |
-0,008524 |
0,168180 |
|
|
|
0 |
3 |
0,244926 |
-0,061631 |
|
|
|
|
|
0 |
4 |
0,562952 |
0,428178 |
|
|
|
5 |
3 |
0,1 |
1 |
-0,047745 |
-0,286509 |
|
|
|
|
|
0 |
2 |
0,065149 |
-0,212927 |
|
|
|
|
|
0,1 |
3 |
0,982596 |
0,499436 |
|
|
|
5 |
2 |
0,1 |
1 |
-0,350815 |
-0,440553 |
0,461576 |
0,437384 |
|
|
|
0,2 |
2 |
1,350315 |
0,440553 |
|
|
|
5 |
3 |
0 |
1 |
-0,072305 |
-0,251774 |
|
|
|
|
|
0,2 |
2 |
0,328610 |
-0,150289 |
0,101718 |
0,238717 |
|
|
|
0 |
3 |
0,743694 |
0,402063 |
|
|
|
5 |
3 |
0,2 |
1 |
0,068985 |
-0,256714 |
|
|
|
|
|
0 |
2 |
0,187762 |
-0,152185 |
0,044423 |
0,211617 |
|
|
|
0 |
3 |
0,743253 |
0,408898 |
|
|
|
5 |
2 |
0,2 |
1 |
-0,190188 |
-0,399297 |
0,369056 |
0,390213 |
|
|
|
0,1 |
2 |
1,190188 |
0,399297 |
|
|
|
5 |
3 |
0,1 |
1 |
-0,012089 |
-0,255785 |
|
|
|
|
|
0,1 |
2 |
0,271262 |
-0,148321 |
0,077686 |
0,227980 |
|
|
|
0 |
3 |
0,740827 |
0,404106 |
|
|
|
5 |
2 |
0,3 |
1 |
0,030761 |
-0,339552 |
0,236740 |
0,316889 |
|
|
|
0 |
2 |
0,969239 |
0,339552 |
|
|
|
6 |
6 |
0 |
1 |
0,044826 |
-0,128810 |
|
|
|
|
|
0 |
2 |
0,079377 |
-0,132102 |
|
|
|
|
|
0 |
3 |
0,117541 |
-0,111951 |
-0,027715 |
0,116576 |
|
|
|
0 |
4 |
0,163591 |
-0,064666 |
|
|
|
|
|
0 |
5 |
0,226486 |
0,031796 |
|
|
|
|
|
0 |
6 |
0,368179 |
0,405733 |
|
|
|
6 |
4 |
0,1 |
1 |
0,008831 |
-0,197752 |
|
|
|
|
|
0 |
2 |
0,058664 |
-0,172042 |
0,031981 |
0,171998 |
|
|
|
0,1 |
3 |
0,345722 |
-0,026586 |
|
|
|
|
|
0 |
4 |
0,586783 |
0,396381 |
|
|
|
6 |
4 |
0,1 |
1 |
0,023519 |
-0,186303 |
|
|
|
|
|
0,1 |
2 |
0,160097 |
-0,162342 |
0,018605 |
0,160547 |
|
|
|
0 |
3 |
0,216754 |
-0,059748 |
|
|
|
|
|
0 |
4 |
0,599629 |
0,408393 |
|
|
|
6 |
3 |
0,1 |
1 |
-0,112093 |
-0,278666 |
|
|
|
|
|
0,1 |
2 |
0,119136 |
-0,190239 |
0,159263 |
0,256346 |
|
|
|
0,1 |
3 |
0,992955 |
0,468904 |
|
|
|
6 |
4 |
0 |
1 |
-0,036039 |
-0,195636 |
|
|
|
|
|
0 |
2 |
0,017906 |
-0,184670 |
0,054110 |
0,183434 |
|
|
|
0,2 |
3 |
0,426864 |
-0,011361 |
|
|
|
|
|
* |
* |
0,591269 |
0,391668 |
|
|
|
_______________ | |||||||
|
6 |
4 |
0 |
1 |
-0,009765 |
-0,175372 |
|
|
|
|
|
0,2 |
2 |
0,195808 |
-0,171222 |
0,028875 |
0,163138 |
|
|
|
0 |
3 |
0,204217 |
-0,062816 |
|
|
|
|
|
0 |
4 |
0,609641 |
0,409410 |
|
|
|
6 |
3 |
0 |
1 |
-0,161756 |
-0,277443 |
|
|
|
|
|
0,2 |
2 |
0,170932 |
-0,187928 |
0,183254 |
0,266813 |
|
|
|
0,1 |
3 |
0,990824 |
0,465371 |
|
|
|
6 |
4 |
0,2 |
1 |
0,066540 |
-0,197410 |
|
|
|
|
|
0 |
2 |
0,111241 |
-0,154334 |
0,004657 |
0,156421 |
|
|
|
0 |
3 |
0,233432 |
-0,055395 |
|
|
|
|
|
0 |
4 |
0,588787 |
0,407139 |
|
|
|
6 |
3 |
0,2 |
1 |
-0,049611 |
-0,277728 |
|
|
|
|
|
0 |
2 |
0,049304 |
-0,197163 |
0,128792 |
0,242259 |
|
|
|
0,1 |
3 |
1,000307 |
0,474890 |
|
|
|
6 |
2 |
0,2 |
1 |
-0,352206 |
-0,421383 |
0,494420 |
0,415839 |
|
|
|
0,2 |
2 |
1,352206 |
0,421383 |
|
|
|
6 |
3 |
0,1 |
1 |
-0,069401 |
-0,245965 |
|
|
|
|
|
0,2 |
2 |
0,306555 |
-0,137608 |
0,118452 |
0,223278 |
|
|
|
0 |
3 |
0,762846 |
0,383573 |
|
|
|
6 |
3 |
0,2 |
1 |
-0,012161 |
-0,249133 |
|
|
|
|
|
0,1 |
2 |
0,251241 |
-0,136313 |
0,094017 |
0,213013 |
|
|
|
0 |
3 |
0,760920 |
0,385446 |
|
|
|
6 |
3 |
0 |
1 |
-0,114799 |
-0,241433 |
|
|
|
|
|
0,3 |
2 |
0,348115 |
-0,348115 |
0,137267 |
0,230648 |
|
|
|
0 |
3 |
0,766683 |
0,382692 |
|
|
|
6 |
3 |
0,3 |
1 |
0,065156 |
-0,249313 |
|
|
|
|
|
0 |
2 |
0,170061 |
-0,140648 |
0,060290 |
0,197481 |
|
|
|
0 |
3 |
0,764783 |
0,389961 |
|
|
|
6 |
2 |
0,3 |
1 |
-0,195708 |
-0,382326 |
0,398546 |
0,369957 |
|
|
|
0,1 |
2 |
1,195708 |
0,382326 |
|
|
|
6 |
2 |
0,4 |
1 |
0,019977 |
-0,325860 |
0,261817 |
0,299366 |
|
|
|
0 |
2 |
0,980023 |
0,325860 |
|
|
|
6 |
5 |
0 |
1 |
0,007521 |
-0,169920 |
|
|
|
|
|
0 |
2 |
0,048328 |
-0,166319 |
|
|
|
|
|
0 |
3 |
0,101608 |
-0,129510 |
0,008880 |
0,156905 |
|
|
|
0 |
4 |
0,172859 |
-0,054453 |
|
|
|
|
|
0,1 |
5 |
0,669685 |
0,520201 |
|
|
|
6 |
4 |
0 |
1 |
-0,063569 |
-0,225141 |
|
|
|
|
|
0 |
2 |
-0,006726 |
-0,209083 |
0,08035 |
0,212422 |
|
|
|
0 |
3 |
0,079882 |
-0,146386 |
|
|
|
|
|
0,2 |
4 |
0,990412 |
0,580610 |
|
|
|
6 |
3 |
0 |
1 |
-0,211474 |
-0,311847 |
|
|
|
|
|
0 |
2 |
-0,112994 |
-0,271381 |
0,232696 |
0,301732 |
|
|
|
0,3 |
3 |
1,324468 |
0,583229 |
|
|
|
6 |
2 |
0 |
1 |
-0,588298 |
-0,477782 |
0,631489 |
0,477340 |
|
|
|
0,4 |
2 |
1,588298 |
0,477782 |
|
|
|
6 |
5 |
0 |
1 |
0,013939 |
-0,159149 |
|
|
|
|
|
0 |
2 |
0,054654 |
-0,156823 |
|
|
|
|
|
0 |
3 |
0,106415 |
-0,123795 |
0,029984 |
0,146562 |
|
|
|
0,1 |
4 |
0,362619 |
0,046088 |
|
|
|
|
|
0 |
5 |
0,462373 |
0,393678 |
|
|
|
6 |
5 |
0 |
1 |
0,020733 |
-0,150942 |
|
|
|
|
|
0 |
2 |
0,061138 |
-0,149874 |
|
|
|
|
|
0,1 |
3 |
0,221969 |
-0,098017 |
-0,003302 |
0,138563 |
|
|
|
0 |
4 |
0,221097 |
-0,011326 |
|
|
|
|
|
0 |
5 |
0,475063 |
0,410160 |
|
|
|
6 |
4 |
0 |
1 |
-0,053485 |
-0,215020 |
|
|
|
|
|
0 |
2 |
0,002117 |
-0,200832 |
0,070668 |
0,202429 |
|
|
|
0,1 |
3 |
0,244120 |
-0,078892 |
|
|
|
|
|
0,1 |
4 |
0,807248 |
0,494744 |
|
|
|
6 |
5 |
0 |
1 |
0,027683 |
-0,145994 |
|
|
|
|
|
0,1 |
2 |
0,126713 |
-0,156106 |
|
|
|
|
|
0 |
3 |
0,140815 |
-0,103496 |
-0,009823 |
0,133605 |
|
|
|
0 |
4 |
0,231656 |
-0,004763 |
|
|
|
|
|
0 |
5 |
0,473133 |
0,410358 |
|
|
|
6 |
4 |
0 |
1 |
-0,040673 |
-0,205281 |
|
|
|
|
|
0,1 |
2 |
0,086730 |
-0,190784 |
0,304716 |
0,192644 |
|
|
|
0 |
3 |
0,130920 |
-0,112078 |
|
|
|
|
|
0,1 |
4 |
0,823023 |
0,508143 |
|
|
|
6 |
3 |
0 |
1 |
-0,190667 |
-0,297888 |
|
|
|
|
|
0,1 |
2 |
0,021498 |
-0,231059 |
0,211910 |
0,287517 |
|
|
|
0,2 |
3 |
1,169168 |
0,528947 |
|
|
|
6 |
5 |
0,1 |
1 |
0,056925 |
-0,158875 |
|
|
|
|
|
0 |
2 |
0,091381 |
-0,144922 |
|
|
|
|
|
0 |
3 |
0,150681 |
0,102910 |
-0,017433 |
0,132694 |
|
|
|
0 |
4 |
0,239715 |
-0,002716 |
|
|
|
|
|
0 |
5 |
0,461928 |
0,409423 |
|
|
|
6 |
3 |
0,1 |
1 |
-0,137983 |
-0,296928 |
|
|
|
|
|
0 |
2 |
-0,039253 |
-0,238187 |
0,184692 |
0,275156 |
|
|
|
0,2 |
3 |
1,177236 |
0,535115 |
|
|
|
6 |
4 |
0,1 |
1 |
-0,005788 |
-0,214536 |
|
|
|
|
|
0 |
2 |
0,046557 |
-0,184705 |
0,044942 |
0,188056 |
|
|
|
0 |
3 |
0,143920 |
-0,108911 |
|
|
|
|
|
0,1 |
4 |
0,815311 |
0,508151 |
|
|
|
6 |
2 |
0,1 |
1 |
-0,479380 |
-0,452110 |
0,569464 |
0,450055 |
|
|
|
0,3 |
2 |
1,479380 |
0,452110 |
|
|
|
6 |
4 |
0 |
1 |
-0,025177 |
-0,187606 |
|
|
|
|
|
0,1 |
2 |
0,099938 |
-0,178787 |
0,043607 |
0,175361 |
|
|
|
0,1 |
3 |
0,328356 |
-0,031369 |
|
|
|
|
|
0 |
4 |
0,596883 |
0,397762 |
|
|
Примечания:
1. В графе 3: 0 - отказ; 1, 2, 3, 4, 5 - цензурирования.
2. Коэффициенты , 
, 
, 
определяют в зависимости от чередования отказов и цензурирований: наработки до отказа и до цензурирования выстраивают в общий вариационный ряд по возрастанию наработок; каждому отказу присваивают символ 0; каждое цензурирование совмещают с ближайшим предшествующим в вариационном ряду отказом; группе цензурирований (одному или нескольким), совмещенных с рассматриваемым отказом, присваивают символ 1, ..., 5, равный числу цензурирований; последовательность символов 0 и 1, ..., 5 образует чередование отказов и цензурирований.
Таблица 63
Коэффициенты , для определения точечных оценок параметров
распределения Вейбулла (
15)
|
|
|
|
|
|
2 |
1 |
0,110731 |
-0,421383 |
|
|
2 |
0,889269 |
0,421383 |
|
3 |
1 |
-0,166001 |
-0,452110 |
|
|
2 |
1,166001 |
0,452110 |
|
3 |
1 |
0,081063 |
-0,278666 |
|
|
2 |
0,251001 |
-0,190239 |
|
|
3 |
0,667936 |
0,468904 |
|
4 |
1 |
-0,346974 |
-0,465455 |
|
|
2 |
1,346974 |
0,465455 |
|
4 |
1 |
-0,044975 |
-0,297651 |
|
|
2 |
0,088057 |
-0,234054 |
|
|
3 |
0,956918 |
0,531705 |
|
4 |
1 |
0,64336 |
-0,203052 |
|
|
2 |
0,147340 |
-0,182749 |
|
|
3 |
0,261510 |
-0,070109 |
|
|
4 |
0,526813 |
0,455910 |
|
5 |
1 |
-0,481434 |
-0,472962 |
|
|
2 |
1,481434 |
0,472962 |
|
5 |
1 |
-0,137958 |
-0,306562 |
|
|
2 |
-0,025510 |
-0,257087 |
|
|
3 |
1,163468 |
0,563650 |
|
5 |
1 |
-0,006983 |
-0,217766 |
|
|
2 |
0,059652 |
-0,199351 |
|
|
3 |
0,156664 |
-0,118927 |
|
|
4 |
0,790668 |
0,536044 |
|
5 |
1 |
0,052975 |
-0,158131 |
|
|
2 |
0,103531 |
-0,155707 |
|
|
3 |
0,163808 |
-0,111820 |
|
|
4 |
0,246092 |
-0,005600 |
|
|
5 |
0,433593 |
0,431259 |
|
6 |
1 |
-0,588298 |
-0,477782 |
|
|
2 |
1,588298 |
0,477782 |
|
6 |
1 |
-0,211474 |
-0,311847 |
|
|
2 |
-0,112994 |
-0,271381 |
|
|
3 |
1,324468 |
0,583229 |
|
6 |
1 |
-0,063569 |
-0,225141 |
|
|
2 |
-0,006726 |
-0,209083 |
|
|
3 |
0,079882 |
-0,146386 |
|
|
4 |
0,990412 |
0,580610 |
|
6 |
1 |
0,007521 |
-0,169920 |
|
|
2 |
0,048328 |
-0,166319 |
|
|
3 |
0,101607 |
-0,129510 |
|
|
4 |
0,172859 |
-0,054453 |
|
|
5 |
0,669695 |
0,520201 |
|
6 |
1 |
0,044826 |
-0,128810 |
|
|
2 |
0,079377 |
-0,132102 |
|
|
3 |
0,117541 |
-0,111951 |
|
|
4 |
0,163591 |
-0,064666 |
|
|
5 |
0,226486 |
0,031796 |
|
|
6 |
0,368179 |
0,405733 |
|
7 |
1 |
-0,676894 |
-0,481140 |
|
|
2 |
1,676894 |
0,481140 |
|
7 |
1 |
-0,272195 |
-0,315309 |
|
|
2 |
-0,184061 |
-0,281139 |
|
|
3 |
1,456255 |
0,596507 |
|
7 |
1 |
-0,110274 |
-0,229091 |
|
|
2 |
-0,060226 |
-0,215613 |
|
|
3 |
0,018671 |
-0,164168 |
|
|
4 |
1,151829 |
0,609472 |
|
7 |
1 |
-0,030368 |
-0,176203 |
|
|
2 |
0,004333 |
-0,172399 |
|
|
3 |
0,052957 |
-0,141218 |
|
|
4 |
0,117599 |
-0,982820 |
|
|
5 |
0,855480 |
0,572640 |
|
7 |
1 |
0,013524 |
-0,138436 |
|
|
2 |
0,041588 |
-0,140342 |
|
|
3 |
0,075499 |
-0,121821 |
|
|
4 |
0,117461 |
-0,082938 |
|
|
5 |
0,172092 |
-0,015394 |
|
|
6 |
0,579835 |
0,498931 |
|
7 |
1 |
0,38743 |
-0,108323 |
|
|
2 |
0,064086 |
-0,113479 |
|
|
3 |
0,090785 |
-0,103569 |
|
|
4 |
0,120971 |
-0,078748 |
|
|
5 |
0,157657 |
-0,032632 |
|
|
6 |
0,207825 |
0,054727 |
|
|
7 |
0,319934 |
0,382022 |
|
8 |
1 |
-0,752513 |
-0,483616 |
|
|
2 |
1,752513 |
0,483616 |
|
8 |
1 |
-0,323875 |
-0,317890 |
|
|
2 |
-0,243808 |
-0,288231 |
|
|
3 |
1,567683 |
0,806120 |
|
8 |
1 |
-0,149973 |
-0,232805 |
|
|
2 |
-0,105015 |
-0,220324 |
|
|
3 |
-0,032357 |
-0,176575 |
|
|
4 |
1,287245 |
0,629805 |
|
8 |
1 |
-0,062656 |
-0,180231 |
|
|
2 |
-0,032248 |
-0,176510 |
|
|
3 |
0,012767 |
-0,149566 |
|
|
4 |
0,072446 |
-0,101642 |
|
|
5 |
1,009691 |
0,607948 |
|
8 |
1 |
-0,013509 |
-0,143834 |
|
|
2 |
0,010292 |
-0,145006 |
|
|
3 |
0,041357 |
-0,128393 |
|
|
4 |
0,080475 |
-0,095696 |
|
|
5 |
0,130327 |
-0,043280 |
|
|
6 |
0,751058 |
0,556209 |
|
8 |
1 |
0,015973 |
-0,116317 |
|
|
2 |
0,036729 |
-0,120331 |
|
|
3 |
0,060439 |
-0,110582 |
|
|
4 |
0,088239 |
-0,088450 |
|
|
5 |
0,122062 |
-0,050995 |
|
|
6 |
0,165529 |
0,009700 |
|
|
7 |
0,511030 |
0,476975 |
|
8 |
1 |
0,034052 |
-0,093270 |
|
|
2 |
0,053552 |
-0,098886 |
|
|
3 |
0,073452 |
-0,093994 |
|
|
4 |
0,095062 |
-0,079752 |
|
|
5 |
0,119768 |
-0,053918 |
|
|
6 |
0,149934 |
-0,010179 |
|
|
7 |
0,191236 |
0,069325 |
|
|
8 |
0,282943 |
0,360675 |
|
9 |
1 |
-0,818444 |
-0,485517 |
|
|
2 |
1,818444 |
0,485517 |
|
9 |
1 |
-0,368833 |
-0,319786 |
|
|
2 |
-0,295280 |
-0,293621 |
|
|
3 |
1,664113 |
0,613407 |
|
9 |
1 |
-0,184461 |
-0,235080 |
|
|
2 |
-0,143505 |
-0,273891 |
|
|
3 |
-0,075815 |
-0,185970 |
|
|
4 |
1,403781 |
0,644941 |
|
9 |
1 |
-0,090726 |
-0,183061 |
|
|
2 |
-0,063541 |
-0,179515 |
|
|
3 |
-0,021495 |
-0,155825 |
|
|
4 |
0,034159 |
-0,115133 |
|
|
5 |
1,141604 |
0,633534 |
|
9 |
1 |
-0,037118 |
-0,147411 |
|
|
2 |
-0,016377 |
-0,148150 |
|
|
3 |
0,012499 |
-0,133219 |
|
|
4 |
0,049305 |
-0,105060 |
|
|
5 |
0,095614 |
-0,062073 |
|
|
6 |
0,896078 |
0,595913 |
|
9 |
1 |
-0,004220 |
-0,120988 |
|
|
2 |
0,013386 |
-0,124245 |
|
|
3 |
0,035068 |
-0,115091 |
|
|
4 |
0,061198 |
-0,095508 |
|
|
5 |
0,093013 |
-0,064162 |
|
|
6 |
0,132740 |
-0,017187 |
|
|
7 |
0,668315 |
0,537180 |
|
9 |
1 |
0,016797 |
-0,100011 |
|
|
2 |
0,032919 |
-0,104750 |
|
|
3 |
0,050582 |
-0,099608 |
|
|
4 |
0,070497 |
-0,086226 |
|
|
5 |
0,093635 |
-0,063541 |
|
|
6 |
0,121560 |
- 0,028346 |
|
|
7 |
0,157175 |
0,026525 |
|
|
8 |
0,456836 |
0,455956 |
|
9 |
1 |
0,030338 |
-0,081777 |
|
|
2 |
0,045872 |
-0,087308 |
|
|
3 |
0,061368 |
-0,085084 |
|
|
4 |
0,077742 |
-0,076470 |
|
|
5 |
0,095769 |
-0,060667 |
|
|
6 |
0,116517 |
-0,035136 |
|
|
7 |
0,141932 |
0,006001 |
|
|
8 |
0,176764 |
0,078828 |
|
|
9 |
0,253697 |
0,341614 |
|
10 |
1 |
-0,876869 |
-0,487022 |
|
|
2 |
1,876869 |
0,487022 |
|
10 |
1 |
-0,408602 |
-0,321265 |
|
|
2 |
-0,340443 |
-0,297858 |
|
|
3 |
1,749045 |
0,619124 |
|
10 |
1 |
-0,214930 |
-0,236817 |
|
|
2 |
-0,177223 |
-0,226688 |
|
|
3 |
-0,113820 |
-0,193159 |
|
|
4 |
1,505973 |
0,656663 |
|
10 |
1 |
-0,115524 |
-0,185169 |
|
|
2 |
-0,090868 |
-0,181821 |
|
|
3 |
-0,051341 |
-0,160697 |
|
|
4 |
0,000925 |
-0,125311 |
|
|
5 |
1,256809 |
0,652997 |
|
10 |
1 |
-0,058017 |
-0,149985 |
|
|
2 |
-0,039595 |
-0,150451 |
|
|
3 |
-0,012513 |
-0,136941 |
|
|
4 |
0,022314 |
-0,112224 |
|
|
5 |
0,022062 |
-0,075721 |
|
|
6 |
1,065750 |
0,625321 |
|
10 |
1 |
-0,022198 |
-0,124170 |
|
|
2 |
-0,006909 |
-0,126894 |
|
|
3 |
0,013224 |
-0,118392 |
|
|
4 |
0,037994 |
-0,100924 |
|
|
5 |
0,068153 |
-0,073988 |
|
|
6 |
0,105064 |
-0,035501 |
|
|
7 |
0,804572 |
0,579868 |
|
10 |
1 |
0,001179 |
-0,104082 |
|
|
2 |
0,014869 |
-0,108163 |
|
|
3 |
0,030998 |
-0,103119 |
|
|
4 |
0,049734 |
-0,090835 |
|
|
5 |
0,071745 |
-0,070902 |
|
|
6 |
0,098114 |
-0,041560 |
|
|
7 |
0,130649 |
0,000799 |
|
|
8 |
-0,602692 |
0,517864 |
|
10 |
1 |
0,016841 |
-0,087538 |
|
|
2 |
0,029807 |
-0,092405 |
|
|
3 |
0,043570 |
-0,089839 |
|
|
4 |
0,058640 |
-0,081428 |
|
|
5 |
0,075576 |
-0,066855 |
|
|
6 |
0,095169 |
-0,044670 |
|
|
7 |
0,118707 |
-0,011816 |
|
|
8 |
0,148575 |
0,038159 |
|
|
9 |
0,413116 |
0,436394 |
|
10 |
1 |
0,027331 |
-0,072734 |
|
|
2 |
0,040034 |
-0,077971 |
|
|
3 |
0,052496 |
-0,077242 |
|
|
4 |
0,065408 |
-0,071876 |
|
|
5 |
0,072963 |
-0,061652 |
|
|
6 |
0,094638 |
-0,045420 |
|
|
7 |
0,112414 |
-0,020698 |
|
|
8 |
0,134239 |
0,017927 |
|
|
9 |
0,164178 |
0,085070 |
|
|
10 |
0,230001 |
0,324597 |
|
11 |
1 |
-0,929310 |
-0,488243 |
|
|
2 |
1,929310 |
0,488243 |
|
11 |
1 |
-0,444245 |
-0,322452 |
|
|
2 |
-0,380642 |
-0,301277 |
|
|
3 |
1,824887 |
0,623729 |
|
11 |
1 |
-0,242206 |
-0,238188 |
|
|
2 |
-0,207204 |
-0,228941 |
|
|
3 |
-0,147490 |
-0,198888 |
|
|
4 |
1,596900 |
0,666017 |
|
11 |
1 |
-0,137718 |
-0,186803 |
|
|
2 |
-0,115110 |
-0,183651 |
|
|
3 |
-0,077762 |
-0,164597 |
|
|
4 |
-0,028411 |
-0,133278 |
|
|
5 |
1,359000 |
0,668329 |
|
11 |
1 |
-0,076739 |
-0,151936 |
|
|
2 |
-0,060142 |
-0,152227 |
|
|
3 |
-0,034581 |
-0,139907 |
|
|
4 |
-0,001490 |
-0,117886 |
|
|
5 |
0,039518 |
-0,086311 |
|
|
6 |
1,133134 |
0,648081 |
|
11 |
1 |
-0,038849 |
-0,126507 |
|
|
2 |
-0,024842 |
-0,128838 |
|
|
3 |
-0,005964 |
-0,120951 |
|
|
4 |
0,017632 |
-0,105219 |
|
|
5 |
0,046354 |
-0,081602 |
|
|
6 |
0,081182 |
-0,018929 |
|
|
7 |
0,923987 |
0,612017 |
|
11 |
1 |
-0,012943 |
-0,106922 |
|
|
2 |
-0,001050 |
-0,110198 |
|
|
3 |
0,013809 |
-0,105662 |
|
|
4 |
0,031661 |
-0,094405 |
|
|
5 |
0,052723 |
-0,076693 |
|
|
6 |
0,077815 |
-0,051525 |
|
|
7 |
0,108161 |
-0,016860 |
|
|
8 |
0,729765 |
0,562564 |
|
11 |
1 |
0,004425 |
-0,091125 |
|
|
2 |
0,015498 |
-0,095437 |
|
|
3 |
0,028073 |
-0,092780 |
|
|
4 |
0,042178 |
-0,084833 |
|
|
5 |
0,058340 |
-0,071581 |
|
|
6 |
0,077093 |
-0,052182 |
|
|
7 |
0,099349 |
-0,024880 |
|
|
8 |
0,126592 |
0,013606 |
|
|
9 |
0,548502 |
0,499201 |
|
11 |
1 |
0,016502 |
-0,077717 |
|
|
2 |
0,027205 |
-0,082449 |
|
|
3 |
0,038291 |
-0,081388 |
|
|
4 |
0,050160 |
-0,075977 |
|
|
5 |
0,063170 |
-0,066222 |
|
|
6 |
0,077772 |
-0,030120 |
|
|
7 |
0,114811 |
0,000537 |
|
|
8 |
0,094625 |
-0,051429 |
|
|
9 |
0,140333 |
0,046381 |
|
|
10 |
0,377130 |
0,418384 |
|
11 |
1 |
0,024850 |
-0,065444 |
|
|
2 |
0,035456 |
-0,070318 |
|
|
3 |
0,045727 |
-0,070456 |
|
|
4 |
0,056215 |
-0,067076 |
|
|
5 |
0,067261 |
-0,060207 |
|
|
6 |
0,079220 |
-0,049800 |
|
|
7 |
0,092560 |
-0,033156 |
|
|
8 |
0,108034 |
-0,009427 |
|
|
9 |
0,127088 |
0,026879 |
|
|
10 |
0,153197 |
0,089148 |
|
|
11 |
0,210412 |
0,309357 |
|
12 |
1 |
-0,976872 |
-0,489254 |
|
|
2 |
1,976872 |
0,459254 |
|
12 |
1 |
-0,476530 |
-0,323426 |
|
|
2 |
-0,416886 |
-0,301093 |
|
|
3 |
1,893367 |
0,627519 |
|
12 |
1 |
-0,266888 |
-0,239300 |
|
|
2 |
-0,234180 |
-0,230796 |
|
|
3 |
-0,177681 |
-0,202362 |
|
|
4 |
1,678749 |
0,673657 |
|
12 |
1 |
-0,157792 |
-0,188109 |
|
|
2 |
-0,136884 |
-0,185142 |
|
|
3 |
-0,101445 |
-0,167790 |
|
|
4 |
-0,054640 |
-0,139623 |
|
|
5 |
1,450761 |
0,689734 |
|
12 |
1 |
-0,093679 |
-0,153471 |
|
|
2 |
-0,078561 |
-0,153632 |
|
|
3 |
-0,054320 |
-0,142329 |
|
|
4 |
-0,022769 |
-0,122474 |
|
|
5 |
0,016136 |
-0,094355 |
|
|
6 |
1,233193 |
0,666261 |
|
12 |
1 |
-0,052987 |
-0,128808 |
|
|
2 |
-0,040893 |
-0,130339 |
|
|
3 |
-0,023072 |
-0,123007 |
|
|
4 |
-0,000515 |
-0,108712 |
|
|
5 |
0,026960 |
-0,087681 |
|
|
6 |
0,059918 |
-0,059256 |
|
|
7 |
1,030620 |
0,637307 |
|
12 |
1 |
-0,025785 |
-0,109045 |
|
|
2 |
-0,015312 |
-0,112242 |
|
|
3 |
-0,001353 |
-0,107627 |
|
|
4 |
0,015634 |
-0,097267 |
|
|
5 |
0,035853 |
-0,081361 |
|
|
6 |
0,059835 |
-0,059315 |
|
|
7 |
0,088444 |
-0,029900 |
|
|
8 |
0,842654 |
0,586748 |
|
12 |
1 |
-0,006944 |
-0,093650 |
|
|
2 |
0,002669 |
-0,097540 |
|
|
3 |
0,014239 |
-0,094893 |
|
|
4 |
0,027669 |
-0,087418 |
|
|
5 |
0,043189 |
-0,075371 |
|
|
6 |
0,061225 |
-0,058180 |
|
|
7 |
0,082441 |
-0,034802 |
|
|
8 |
0,107856 |
-0,003342 |
|
|
9 |
0,667655 |
0,545234 |
|
12 |
1 |
0,006411 |
-0,080881 |
|
|
2 |
0,015598 |
-0,085171 |
|
|
3 |
0,025675 |
-0,083952 |
|
|
4 |
0,036799 |
-0,078714 |
|
|
5 |
0,049211 |
-0,069510 |
|
|
6 |
0,063256 |
-0,056237 |
|
|
7 |
0,079438 |
-0,037675 |
|
|
8 |
0,098522 |
-0,012272 |
|
|
9 |
0,121752 |
0,022956 |
|
|
10 |
0,503338 |
0,481555 |
|
12 |
1 |
0,015982 |
-0,069798 |
|
|
2 |
0,024997 |
-0,074285 |
|
|
3 |
0,034156 |
-0,074131 |
|
|
4 |
0,043790 |
-0,070617 |
|
|
5 |
0,054149 |
-0,063891 |
|
|
6 |
0,065515 |
-0,033621 |
|
|
7 |
0,078264 |
-0,039034 |
|
|
8 |
0,692958 |
-0,018718 |
|
|
9 |
0,110521 |
0,009948 |
|
|
10 |
0,132666 |
0,052280 |
|
|
11 |
0,347003 |
0,401864 |
|
12 |
1 |
0,022771 |
-0,059449 |
|
|
2 |
0,031776 |
-0,063952 |
|
|
3 |
0,040408 |
-0,064601 |
|
|
4 |
0,059122 |
-0,052489 |
|
|
5 |
0,058175 |
-0,057754 |
|
|
6 |
0,067800 |
-0,050137 |
|
|
7 |
0,078281 |
-0,039010 |
|
|
8 |
0,090017 |
-0,023199 |
|
|
9 |
0,103664 |
-0,000505 |
|
|
10 |
0,120475 |
0,033695 |
|
|
11 |
0,143566 |
0,091751 |
|
|
12 |
0,193917 |
0,295648 |
|
13 |
1 |
- 1,020378 |
-0,490105 |
|
|
2 |
2,020378 |
0,490105 |
|
13 |
1 |
-0,506034 |
-0,324239 |
|
|
2 |
-0,449735 |
-0,306454 |
|
|
3 |
1,955765 |
0,630694 |
|
13 |
1 |
-0,289420 |
-0,240219 |
|
|
2 |
-0,258687 |
-0,232349 |
|
|
3 |
-0,205024 |
-0,207450 |
|
|
4 |
1,753131 |
0,680018 |
|
13 |
1 |
-0,176109 |
-0,189177 |
|
|
2 |
-0,156637 |
-0,186381 |
|
|
3 |
-0,122893 |
-0,170454 |
|
|
4 |
-0,078337 |
-0,144971 |
|
|
5 |
1,533976 |
0,690983 |
|
13 |
1 |
-0,109140 |
-0,154711 |
|
|
2 |
-0,0925246 |
-0,154785 |
|
|
3 |
-0,072165 |
-0,144347 |
|
|
4 |
-0,041997 |
-0,126268 |
|
|
5 |
-0,004940 |
-0,101028 |
|
|
6 |
1,323488 |
0,681140 |
|
13 |
1 |
-0,066358 |
-0,129743 |
|
|
2 |
-0,055414 |
-0,131538 |
|
|
3 |
-0,038503 |
-0,124701 |
|
|
4 |
-0,16879 |
-0,111609 |
|
|
5 |
0,009416 |
-0,092649 |
|
|
6 |
0,040810 |
-0,067475 |
|
|
7 |
1,126930 |
0,657714 |
|
13 |
1 |
-0,037540 |
-0,110705 |
|
|
2 |
-0,028206 |
-0,113563 |
|
|
3 |
-0,015049 |
-0,109206 |
|
|
4 |
0,001231 |
-0,099644 |
|
|
5 |
0,020686 |
-0,085201 |
|
|
6 |
0,043677 |
-0,065581 |
|
|
7 |
0,070830 |
-0,039995 |
|
|
8 |
0,944372 |
0,623896 |
|
13 |
1 |
-0,017389 |
-0,095590 |
|
|
2 |
-0,008934 |
-0,099109 |
|
|
3 |
0,001863 |
-0,096521 |
|
|
4 |
0,014684 |
-0,089554 |
|
|
5 |
0,029657 |
-0,078690 |
|
|
6 |
0,047027 |
-0,063068 |
|
|
7 |
0,067346 |
-0,042307 |
|
|
8 |
0,091328 |
-0,015928 |
|
|
9 |
0,774437 |
0,580865 |
|
13 |
1 |
-0,002927 |
-0,083170 |
|
|
2 |
0,005067 |
-0,087085 |
|
|
3 |
0,014356 |
-0,057928 |
|
|
4 |
0,024891 |
-0,080789 |
|
|
5 |
0,036816 |
-0,072325 |
|
|
6 |
0,050389 |
-0,060181 |
|
|
7 |
0,065995 |
-0,043768 |
|
|
8 |
0,084201 |
-0,022048 |
|
|
9 |
0,105863 |
0,006715 |
|
|
10 |
0,615348 |
0,528441 |
|
13 |
1 |
0,007623 |
-0,072617 |
|
|
2 |
0,015408 |
-0,076746 |
|
|
3 |
0,023732 |
-0,076418 |
|
|
4 |
0,032743 |
-0,072938 |
|
|
5 |
0,042611 |
-0,066531 |
|
|
6 |
0,053556 |
-0,057014 |
|
|
7 |
0,065876 |
-0,043886 |
|
|
8 |
0,080005 |
-0,026244 |
|
|
9 |
0,096594 |
-0,002552 |
|
|
10 |
0,116703 |
0,029910 |
|
|
11 |
0,465143 |
0,465037 |
|
13 |
1 |
0,015382 |
-0,063288 |
|
|
2 |
0,023100 |
-0,067492 |
|
|
3 |
0,030881 |
-0,067892 |
|
|
4 |
0,038824 |
-0,065622 |
|
|
5 |
0,047302 |
-0,060887 |
|
|
6 |
0,056414 |
-0,053540 |
|
|
7 |
0,066482 |
-0,043158 |
|
|
8 |
0,077739 |
-0,028970 |
|
|
9 |
0,090699 |
-0,009644 |
|
|
10 |
0,106166 |
0,017233 |
|
|
11 |
0,125627 |
0,056547 |
|
|
12 |
0,321416 |
0,386713 |
|
13 |
1 |
0,021005 |
-0,054436 |
|
|
2 |
0,028757 |
-0,058585 |
|
|
3 |
0,036127 |
-0,059535 |
|
|
4 |
0,045501 |
-0,058259 |
|
|
5 |
0,051078 |
-0,054942 |
|
|
6 |
0,059028 |
-0,049472 |
|
|
7 |
0,067533 |
-0,041505 |
|
|
8 |
0,076831 |
-0,030395 |
|
|
9 |
0,087274 |
-0,015037 |
|
|
10 |
0,099441 |
0,006644 |
|
|
11 |
0,114446 |
0,038943 |
|
|
12 |
0,135068 |
0,093324 |
|
|
13 |
0,179913 |
0,283257 |
|
14 |
1 |
-1,060461 |
-0,490831 |
|
|
2 |
2,060461 |
0,490831 |
|
14 |
1 |
-0,533158 |
-0,324929 |
|
|
2 |
-0,479874 |
-0,808462 |
|
|
3 |
2,013058 |
0,633913 |
|
14 |
1 |
-0,310144 |
- 0,240992 |
|
|
2 |
-0,281132 |
-0,233670 |
|
|
3 |
-0,229990 |
-0,210735 |
|
|
4 |
1,321236 |
0,685397 |
|
14 |
1 |
-0,192947 |
-0,190068 |
|
|
2 |
-0,174709 |
-0,187427 |
|
|
3 |
-0,142478 |
-0,172710 |
|
|
4 |
-0,099930 |
-0,049393 |
|
|
5 |
1,610065 |
0,699598 |
|
14 |
1 |
-0,123352 |
-0,155736 |
|
|
2 |
-0,110490 |
-0,155747 |
|
|
3 |
-0,088443 |
-0,146054 |
|
|
4 |
-0,059523 |
-0,129460 |
|
|
5 |
-0,024111 |
-0,105556 |
|
|
6 |
1,405919 |
0,693553 |
|
14 |
1 |
-0,070656 |
-0,130915 |
|
|
2 |
-0,068666 |
-0,152521 |
|
|
3 |
-0,052554 |
-0,126128 |
|
|
4 |
-0,031776 |
-0,114051 |
|
|
5 |
-0,006522 |
-0,096788 |
|
|
6 |
0,023467 |
0,074184 |
|
|
7 |
1,214708 |
1,674581 |
|
14 |
1 |
-0,048365 |
-0,112041 |
|
|
2 |
-0,039964 |
-0,114637 |
|
|
3 |
-0,027495 |
-0,110509 |
|
|
4 |
0,011849 |
-0,101635 |
|
|
5 |
0,006905 |
-0,088122 |
|
|
6 |
0,029002 |
-0,070735 |
|
|
7 |
0,054897 |
-0,048074 |
|
|
8 |
1,036868 |
0,646052 |
|
14 |
1 |
-0,027030 |
-0,097117 |
|
|
2 |
-0,019516 |
-0,100334 |
|
|
3 |
-0,009363 |
-0,097827 |
|
|
4 |
0,002928 |
-0,091298 |
|
|
5 |
0,017368 |
-0,081103 |
|
|
6 |
0,034165 |
-0,067124 |
|
|
7 |
0,053685 |
-0,048921 |
|
|
8 |
0,076476 |
-0,025720 |
|
|
9 |
0,371287 |
0,609445 |
|
14 |
1 |
-0,011580 |
-0,084931 |
|
|
2 |
-0,004548 |
-0,088528 |
|
|
3 |
0,004100 |
-0,087207 |
|
|
4 |
0,014144 |
-0,082451 |
|
|
5 |
0,025647 |
-0,074573 |
|
|
6 |
0,038794 |
-0,063473 |
|
|
7 |
0,053879 |
-0,048768 |
|
|
8 |
0,071335 |
-0,029776 |
|
|
9 |
0,091783 |
-0,005398 |
|
|
10 |
0,716445 |
0,565105 |
|
14 |
1 |
-0,000170 |
-0,074686 |
|
|
2 |
0,006622 |
-0,078499 |
|
|
3 |
0,014283 |
-0,078064 |
|
|
4 |
0,022800 |
-0,074680 |
|
|
5 |
0,032273 |
-0,068624 |
|
|
6 |
0,042866 |
-0,059816 |
|
|
7 |
0,054817 |
-0,047926 |
|
|
8 |
0,068463 |
-0,032355 |
|
|
9 |
0,084290 |
-0,012126 |
|
|
10 |
0,103025 |
-0,014349 |
|
|
11 |
0,570731 |
0,512429 |
|
14 |
1 |
0,008361 |
-0,065816 |
|
|
2 |
0,015058 |
-0,069728 |
|
|
3 |
0,022076 |
-0,069962 |
|
|
4 |
0,029552 |
-0,067659 |
|
|
5 |
0,037615 |
-0,056130 |
|
|
6 |
0,046411 |
-0,056130 |
|
|
7 |
0,056132 |
-0,046558 |
|
|
8 |
0,067039 |
-0,033834 |
|
|
9 |
0,079506 |
-0,017101 |
|
|
10 |
0,091096 |
0,005064 |
|
|
11 |
0,111723 |
0,035156 |
|
|
12 |
0,432431 |
0,449638 |
|
14 |
1 |
0,014760 |
-0,057849 |
|
|
2 |
0,021453 |
-0,061764 |
|
|
3 |
0,028064 |
-0,062606 |
|
|
4 |
0,034842 |
-0,061074 |
|
|
5 |
0,041933 |
-0,057693 |
|
|
6 |
0,049474 |
-0,052317 |
|
|
7 |
0,057619 |
-0,044707 |
|
|
8 |
0,066569 |
-0,034420 |
|
|
9 |
0,076605 |
-0,020713 |
|
|
10 |
0,088151 |
-0,002338 |
|
|
11 |
0,101914 |
-0,022943 |
|
|
12 |
0,119200 |
0,059643 |
|
|
13 |
0,299416 |
0,372795 |
|
14 |
1 |
0,019487 |
-0,050186 |
|
|
2 |
0,026238 |
-0,054008 |
|
|
3 |
0,032614 |
-0,055130 |
|
|
4 |
0,038947 |
-0,054419 |
|
|
5 |
0,045399 |
-0,052075 |
|
|
6 |
0,052097 |
-0,048066 |
|
|
7 |
0,059168 |
-0,042197 |
|
|
8 |
0,066767 |
-0,034099 |
|
|
9 |
0,075102 |
-0,023149 |
|
|
10 |
0,084482 |
-0,008285 |
|
|
11 |
0,095428 |
0,012430 |
|
|
12 |
0,108942 |
0,043015 |
|
|
13 |
0,127523 |
0,094166 |
|
|
14 |
0,167807 |
0,272004 |
|
15 |
1 |
- 1,097617 |
-0,491458 |
|
|
2 |
2,097617 |
0,491458 |
|
15 |
1 |
-0,558336 |
-0,325521 |
|
|
2 |
-0,607671 |
-0,310191 |
|
|
3 |
2,066007 |
0,635712 |
|
15 |
1 |
-0,329324 |
-0,241651 |
|
|
2 |
-0,301829 |
-0,234807 |
|
|
3 |
-0,252948 |
-0,213548 |
|
|
4 |
1,884101 |
0,690005 |
|
15 |
1 |
-0,136198 |
-0,156597 |
|
|
2 |
-0,124518 |
-0,156563 |
|
|
3 |
-0,103401 |
-0,147517 |
|
|
4 |
-0,075614 |
-0,132182 |
|
|
5 |
-0,041680 |
-0,111215 |
|
|
6 |
1,481712 |
0,704074 |
|
15 |
1 |
-0,208525 |
-0,190823 |
|
|
2 |
-0,191357 |
-0,188323 |
|
|
3 |
-0,160491 |
-0,174645 |
|
|
4 |
-0,119748 |
-0,153153 |
|
|
5 |
1,689121 |
0,706944 |
|
15 |
1 |
-0,090036 |
-0,131891 |
|
|
2 |
-0,080850 |
-0,133342 |
|
|
3 |
-0,065446 |
-0,127335 |
|
|
4 |
-0,045441 |
-0,116138 |
|
|
5 |
-0,021137 |
-0,100291 |
|
|
6 |
0,007597 |
-0,079774 |
|
|
7 |
1,295312 |
0,688771 |
|
15 |
1 |
-0,058390 |
-0,113143 |
|
|
2 |
-0,050767 |
-0,115520 |
|
|
3 |
-0,038897 |
-0,111607 |
|
|
4 |
-0,023825 |
-0,103332 |
|
|
5 |
-0,005717 |
-0,091156 |
|
|
6 |
0,015565 |
-0,075053 |
|
|
7 |
0,040351 |
-0,054703 |
|
|
8 |
1,121680 |
0,664514 |
|
15 |
1 |
-0,035972 |
-0,098361 |
|
|
2 |
-0,029235 |
-0,101322 |
|
|
3 |
-0,019633 |
-0,098904 |
|
|
4 |
-0,007812 |
-0,092773 |
|
|
5 |
0,006156 |
-0,083327 |
|
|
6 |
0,022403 |
-0,070544 |
|
|
7 |
0,041203 |
-0,054142 |
|
|
8 |
0,062969 |
-0,033595 |
|
|
9 |
0,959920 |
-0,632957 |
|
15 |
1 |
-0,019626 |
-0,086339 |
|
|
2 |
-0,013383 |
-0,089664 |
|
|
3 |
-0,005271 |
-0,088341 |
|
|
4 |
0,004351 |
-0,083828 |
|
|
5 |
0,015475 |
-0,076474 |
|
|
6 |
0,028227 |
-0,066261 |
|
|
7 |
0,042832 |
-0,052943 |
|
|
8 |
0,059624 |
-0,036054 |
|
|
9 |
0,079072 |
-0,014863 |
|
|
10 |
0,808700 |
-0,594768 |
|
15 |
1 |
-0,007450 |
-0,076297 |
|
|
2 |
-0,001467 |
-0,079835 |
|
|
3 |
0,005652 |
-0,079332 |
|
|
4 |
0,013759 |
-0,076068 |
|
|
5 |
0,022893 |
-0,070355 |
|
|
6 |
0,033174 |
-0,062181 |
|
|
7 |
0,044787 |
-0,051331 |
|
|
8 |
0,057997 |
-0,037396 |
|
|
9 |
0,073180 |
-0,19723 |
|
|
10 |
0,090865 |
0,002701 |
|
|
11 |
0,666610 |
0,549817 |
|
15 |
1 |
0,001756 |
-0,067695 |
|
|
2 |
0,007624 |
-0,071342 |
|
|
3 |
0,014079 |
-0,071459 |
|
|
4 |
0,021133 |
-0,069178 |
|
|
5 |
0,028861 |
-0,064779 |
|
|
6 |
0,037374 |
-0,058256 |
|
|
7 |
0,046822 |
-0,049425 |
|
|
8 |
0,057431 |
-0,037926 |
|
|
9 |
0,069479 |
-0,023180 |
|
|
10 |
0,083393 |
-0,004280 |
|
|
11 |
0,099799 |
0,020236 |
|
|
12 |
0,532243 |
0,497284 |
|
15 |
1 |
0,008779 |
-0,060130 |
|
|
2 |
0,014620 |
-0,063805 |
|
|
3 |
0,020637 |
-0,064394 |
|
|
4 |
0,026961 |
-0,062900 |
|
|
5 |
0,033693 |
-0,059574 |
|
|
6 |
0,040939 |
-0,054417 |
|
|
7 |
0,048828 |
-0,047269 |
|
|
8 |
0,057528 |
-0,037821 |
|
|
9 |
0,067265 |
-0,025565 |
|
|
10 |
0,078368 |
-0,009694 |
|
|
11 |
0,091330 |
0,011113 |
|
|
12 |
0,106947 |
0,039155 |
|
|
13 |
0,404106 |
0,435302 |
|
15 |
1 |
0,014143 |
-0,053241 |
|
|
2 |
0,020013 |
-0,056789 |
|
|
3 |
0,025750 |
-0,057827 |
|
|
4 |
0,031576 |
-0,056973 |
|
|
5 |
0,037611 |
-0,054542 |
|
|
6 |
0,043958 |
-0,050539 |
|
|
7 |
0,050725 |
-0,044833 |
|
|
8 |
0,058045 |
-0,037157 |
|
|
9 |
0,066092 |
-0,027072 |
|
|
10 |
0,075114 |
-0,013872 |
|
|
11 |
0,085490 |
-0,003612 |
|
|
12 |
0,097344 |
0,027465 |
|
|
13 |
0,113340 |
0,061879 |
|
|
14 |
0,280298 |
0,359950 |
|
15 |
1 |
0,013170 |
-0,046538 |
|
|
2 |
0,024108 |
-0,050064 |
|
|
3 |
0,029685 |
-0,051279 |
|
|
4 |
0,035191 |
-0,050957 |
|
|
5 |
0,040762 |
-0,049298 |
|
|
6 |
0,046496 |
-0,046315 |
|
|
7 |
0,052488 |
-0,041899 |
|
|
8 |
0,058844 |
-0,035827 |
|
|
9 |
0,065696 |
-0,027731 |
|
|
10 |
0,073230 |
-0,017008 |
|
|
11 |
0,081725 |
-0,002653 |
|
|
12 |
0,091651 |
0,017156 |
|
|
13 |
0,103914 |
0,016191 |
|
|
14 |
0,120784 |
0,094483 |
|
|
15 |
0,157255 |
0,261738 |
Таблицa 64
Коэффициенты , для определения точечных оценок параметров нормального распределения
|
|
|
|
|
|
2 |
1 |
0,5000 |
-0,8862 |
|
|
2 |
0,5000 |
0,8862 |
|
3 |
1 |
0,0000 |
-1,1816 |
|
|
2 |
1,0000 |
1,1816 |
|
3 |
1 |
0,3333 |
-0,5908 |
|
|
2 |
0,3333 |
0,0000 |
|
|
3 |
0,3333 |
0,5908 |
|
4 |
1 |
-0,4056 |
-1,3654 |
|
|
2 |
1,4056 |
1,3654 |
|
4 |
1 |
0,1161 |
-0,6971 |
|
|
2 |
0,2408 |
-0,1268 |
|
|
3 |
0,6431 |
0,8239 |
|
4 |
1 |
0,2500 |
-0,4539 |
|
|
2 |
0,2500 |
-0,1102 |
|
|
3 |
0,2500 |
0,1102 |
|
|
4 |
0,2500 |
0,4539 |
|
5 |
1 |
-0,7411 |
-1,4971 |
|
|
2 |
1,7411 |
1,4971 |
|
5 |
1 |
-0,0638 |
-0,7696 |
|
|
2 |
0,1498 |
-0,2121 |
|
|
3 |
0,9139 |
0,9817 |
|
5 |
1 |
0,125 |
-0,5117 |
|
|
2 |
0,183 |
-0,1668 |
|
|
5 |
0,2147 |
0,0274 |
|
|
4 |
0,4771 |
0,6511 |
|
5 |
1 |
0,2000 |
-0,3724 |
|
|
2 |
0,2000 |
-0,1352 |
|
|
3 |
0,2000 |
0,0000 |
|
|
4 |
0,2000 |
0,1352 |
|
|
5 |
0,2000 |
0,3724 |
|
6 |
1 |
-1,0261 |
-1,5988 |
|
|
2 |
2,0261 |
1,5988 |
|
6 |
1 |
-0,2159 |
-0,8244 |
|
|
2 |
0,0649 |
-0,2760 |
|
|
3 |
1,1511 |
1,1004 |
|
6 |
1 |
0,0185 |
-0,5528 |
|
|
2 |
0,1226 |
-0,2091 |
|
|
3 |
0,1761 |
-0,0290 |
|
|
4 |
0,6828 |
0,7909 |
|
6 |
1 |
0,1183 |
-0,4097 |
|
|
2 |
0,1510 |
-0,1685 |
|
|
3 |
0,1680 |
-0,0406 |
|
|
4 |
0,1828 |
0,0740 |
|
|
5 |
0,3799 |
0,5448 |
|
6 |
1 |
0,1667 |
-0,3175 |
|
|
2 |
0,1667 |
-0,1386 |
|
|
3 |
0,1667 |
-0,0432 |
|
|
4 |
0,1667 |
-0,0432 |
|
|
5 |
0,1667 |
0,1386 |
|
|
6 |
0,1667 |
0,3175 |
|
7 |
1 |
-1,2733 |
-1,6812 |
|
|
2 |
2,2733 |
1,6812 |
|
7 |
1 |
-0,3474 |
-0,8682 |
|
|
2 |
-0,0135 |
-0,3269 |
|
|
3 |
1,3609 |
1,1951 |
|
7 |
1 |
-0,0738 |
-0,5848 |
|
|
2 |
0,0677 |
-0,2428 |
|
|
3 |
0,1375 |
-0,0717 |
|
|
4 |
0,8686 |
0,8994 |
|
7 |
1 |
0,0465 |
-0,4370 |
|
|
2 |
0,1072 |
-0,1943 |
|
|
3 |
0,1375 |
0,0718 |
|
|
4 |
0,1626 |
0,0321 |
|
|
5 |
0,5462 |
0,6709 |
|
7 |
1 |
0,1088 |
-0,3440 |
|
|
2 |
0,1295 |
-0,1610 |
|
|
3 |
0,1400 |
-0,0681 |
|
|
4 |
0,1487 |
0,0114 |
|
|
5 |
0,1571 |
0,0901 |
|
|
6 |
0,3159 |
0,4716 |
|
7 |
1 |
0,1429 |
-0,2778 |
|
|
2 |
0,1429 |
-0,1351 |
|
|
3 |
0,1429 |
-0,0625 |
|
|
4 |
0,1429 |
0,0000 |
|
|
5 |
0,1429 |
0,0625 |
|
7 |
6 |
0,1429 |
0,1351 |
|
|
7 |
0,1429 |
0,2778 |
|
8 |
1 |
-1,4915 |
-0,7502 |
|
|
2 |
2,4915 |
1,7502 |
|
8 |
1 |
-0,4632 |
-0,9045 |
|
|
2 |
-0,0855 |
-0,3690 |
|
|
3 |
1,5487 |
1,2735 |
|
8 |
1 |
-0,1549 |
-0,6100 |
|
|
2 |
0,0176 |
-0,2770 |
|
|
3 |
0,1001 |
-0,1061 |
|
|
4 |
1,0372 |
0,9878 |
|
8 |
1 |
-0,0167 |
-0,4586 |
|
|
2 |
0,0617 |
-0,2156 |
|
|
3 |
0,1084 |
-0,0970 |
|
|
4 |
0,1413 |
0,0002 |
|
|
5 |
0,6993 |
0,7709 |
|
8 |
1 |
0,0569 |
-0,3638 |
|
|
2 |
0,0962 |
-0,1788 |
|
|
3 |
0,1153 |
-0,0881 |
|
|
4 |
0,1309 |
-0,0132 |
|
|
5 |
0,1451 |
0,0570 |
|
|
6 |
0,4555 |
0,5868 |
|
8 |
1 |
0,0997 |
-0,2978 |
|
|
2 |
0,1139 |
-0,1515 |
|
|
3 |
0,1208 |
-0,0796 |
|
|
4 |
0,1265 |
-0,0200 |
|
|
5 |
0,1318 |
0,0364 |
|
|
6 |
0,1370 |
0,0951 |
|
|
7 |
0,2704 |
0,4175 |
|
8 |
1 |
0,1250 |
-0,2476 |
|
|
2 |
0,1250 |
-0,1294 |
|
|
3 |
0,1250 |
-0,0713 |
|
|
4 |
0,1250 |
-0,0230 |
|
|
5 |
0,1250 |
0,0230 |
|
|
6 |
0,1250 |
0,0713 |
|
|
7 |
0,1250 |
0,1294 |
|
|
8 |
0,1250 |
0,2476 |
|
9 |
1 |
-1,6868 |
-1,8092 |
|
|
2 |
2,6868 |
1,8092 |
|
9 |
1 |
-0,5664 |
0,9355 |
|
|
2 |
-0,1521 |
-0,4047 |
|
|
3 |
1,7185 |
1,3402 |
|
9 |
1 |
-0,2272 |
0,6330 |
|
|
2 |
-0,0284 |
-0,2944 |
|
|
3 |
0,0644 |
-0,1348 |
|
|
4 |
1,1912 |
1,0622 |
|
9 |
1 |
-0,0731 |
-0,4765 |
|
|
2 |
0,0316 |
-0,2335 |
|
|
3 |
0,0809 |
-0,1181 |
|
|
4 |
0,1199 |
-0,0256 |
|
|
5 |
0,8408 |
0,8537 |
|
9 |
1 |
0,0104 |
-0,3797 |
|
|
2 |
0,0660 |
-0,1936 |
|
|
3 |
0,0923 |
-0,1048 |
|
|
4 |
0,1133 |
-0,0333 |
|
|
5 |
0,1320 |
0,0317 |
|
|
6 |
0,5860 |
0,6797 |
|
9 |
1 |
0,0602 |
-0,3129 |
|
|
2 |
0,0876 |
0,1647 |
|
|
3 |
0,1006 |
-0,0938 |
|
|
4 |
0,1110 |
-0,0364 |
|
|
5 |
0,1204 |
0,0160 |
|
|
6 |
0,1294 |
0,0678 |
|
|
7 |
0,3809 |
0,5239 |
|
9 |
1 |
0,0915 |
-0,2633 |
|
|
2 |
0,1018 |
-0,1421 |
|
|
3 |
0,1067 |
-0,0841 |
|
|
4 |
0,1106 |
-0,0370 |
|
|
5 |
0,1142 |
0,0062 |
|
|
6 |
0,1177 |
0,0492 |
|
|
7 |
0,1212 |
0,0954 |
|
|
8 |
0,2365 |
0,3757 |
|
9 |
1 |
0,1111 |
-0,2237 |
|
|
2 |
0,1111 |
-0,1233 |
|
|
3 |
0,1111 |
-0,0751 |
|
|
4 |
0,1111 |
-0,0360 |
|
|
5 |
0,1111 |
0,0000 |
|
|
6 |
0,1111 |
0,0360 |
|
|
7 |
0,1111 |
0,0751 |
|
|
8 |
0,1111 |
0,1244 |
|
|
9 |
0,1111 |
0,2237 |
|
10 |
1 |
-1,8634 |
-1,8608 |
|
|
2 |
2,8634 |
1,8008 |
|
10 |
1 |
-0,6596 |
-0,9625 |
|
|
2 |
-0,2138 |
-0,4357 |
|
|
3 |
1,8734 |
1,3981 |
|
10 |
1 |
-0,2923 |
-0,6520 |
|
|
2 |
-0,0709 |
-0,3150 |
|
|
3 |
0,0305 |
-0,1593 |
|
|
4 |
1,3327 |
1,1263 |
|
10 |
1 |
-0,1240 |
-0,4919 |
|
|
2 |
0,0016 |
-0,2491 |
|
|
3 |
0,0549 |
-0,1362 |
|
|
4 |
0,0990 |
-0,0472 |
|
|
5 |
0,9716 |
0,9243 |
|
10 |
1 |
-0,0316 |
-0,3930 |
|
|
2 |
0,0383 |
-0,2063 |
|
|
3 |
0,0707 |
-0,1192 |
|
|
4 |
0,0962 |
-0,0501 |
|
|
5 |
0,1185 |
0,0111 |
|
|
6 |
0,7078 |
0,7576 |
|
10 |
1 |
0,0244 |
-0,3252 |
|
|
2 |
0,0636 |
-0,1758 |
|
|
3 |
0,0818 |
-0,1058 |
|
|
4 |
0,0962 |
-0,0502 |
|
|
5 |
0,1089 |
-0,0008 |
|
|
6 |
0,1207 |
0,0469 |
|
|
7 |
0,5045 |
0,6107 |
|
10 |
1 |
0,0605 |
-0,2753 |
|
|
2 |
0,0804 |
-0,1523 |
|
|
3 |
0,0898 |
-0,0947 |
|
|
4 |
0,0972 |
-0,0488 |
|
|
5 |
0,1037 |
-0,0077 |
|
|
6 |
0,1099 |
0,0319 |
|
|
7 |
0,1161 |
0,0722 |
|
|
8 |
0,3424 |
0,4746 |
|
10 |
1 |
0,0843 |
-0,2364 |
|
|
2 |
0,0921 |
-0,1334 |
|
|
3 |
0,0957 |
-0,0851 |
|
|
4 |
0,0986 |
-0,0465 |
|
|
5 |
0,1011 |
-0,0119 |
|
|
6 |
0,1036 |
0,0215 |
|
|
7 |
0,1060 |
0,0559 |
|
|
8 |
0,1085 |
0,0937 |
|
|
9 |
0,2101 |
0,3423 |
|
10 |
1 |
0,1000 |
-0,2044 |
|
|
2 |
0,1000 |
-0,1172 |
|
|
3 |
0,1000 |
-0,0763 |
|
|
4 |
0,1000 |
-0,0436 |
|
|
5 |
0,1000 |
-0,0142 |
|
|
6 |
0,1000 |
0,0142 |
|
|
7 |
0,1000 |
0,0436 |
|
|
8 |
0,1000 |
0,0763 |
|
|
9 |
0,1000 |
0,1172 |
|
|
10 |
0,1000 |
0,2044 |
|
11 |
1 |
-2,0245 |
-1,9065 |
|
|
2 |
3,0245 |
1,9065 |
|
11 |
1 |
-0,7445 |
-0,9882 |
|
|
2 |
-0,2712 |
-0,4630 |
|
|
3 |
2,0157 |
1,4492 |
|
11 |
1 |
-0,3516 |
-0,6657 |
|
|
2 |
-0,1104 |
-0,3331 |
|
|
3 |
-0,0016 |
-0,1807 |
|
|
4 |
1,4636 |
1,1825 |
|
11 |
1 |
-0,1702 |
-0,5053 |
|
|
2 |
-0,0323 |
-0,2627 |
|
|
3 |
0,0303 |
-0,1519 |
|
|
4 |
0,0786 |
-0,0657 |
|
|
5 |
1,0937 |
-0,3357 |
|
11 |
1 |
-0,0698 |
-0,4045 |
|
|
2 |
0,0128 |
-0,2175 |
|
|
3 |
0,0504 |
-0,1317 |
|
|
4 |
0,0797 |
-0,0647 |
|
|
5 |
0,1049 |
-0,0061 |
|
|
6 |
0,8220 |
0,8246 |
|
11 |
1 |
-0,0082 |
-0,3357 |
|
|
2 |
0,0415 |
-0,1854 |
|
|
3 |
0,0642 |
-0,1163 |
|
|
4 |
0,0820 |
-0,0621 |
|
|
5 |
0,0974 |
-0,0146 |
|
|
6 |
0,1116 |
0,0299 |
|
|
7 |
0,6116 |
0,6842 |
|
11 |
1 |
0,0320 |
-0,2852 |
|
|
2 |
0,0609 |
-0,1610 |
|
|
3 |
0,0741 |
-0,1033 |
|
|
4 |
0,0845 |
-0,0589 |
|
|
5 |
0,0935 |
-0,0194 |
|
|
6 |
0,1020 |
0,0178 |
|
|
7 |
0,1101 |
0,0545 |
|
|
8 |
0,4430 |
0,5582 |
|
11 |
1 |
0,0592 |
-0,2463 |
|
|
2 |
0,0744 |
-0,1417 |
|
|
3 |
0,0814 |
-0,0934 |
|
|
4 |
0,0869 |
-0,0555 |
|
|
5 |
0,0917 |
-0,0220 |
|
|
6 |
0,0962 |
0,0095 |
|
|
7 |
0,1005 |
0,0409 |
|
|
8 |
0,1049 |
0,0736 |
|
|
9 |
0,3047 |
0,4349 |
|
11 |
1 |
0,0731 |
-0,2149 |
|
|
2 |
0,0841 |
-0,1256 |
|
|
3 |
0,0869 |
-0,0843 |
|
|
4 |
0,0891 |
-0,0519 |
|
|
5 |
0,0910 |
-0,0233 |
|
|
6 |
0,0928 |
0,0038 |
|
|
7 |
0,0945 |
0,0309 |
|
|
8 |
0,0983 |
0,0593 |
|
|
9 |
0,0982 |
0,0911 |
|
|
10 |
0,1891 |
0,3149 |
|
11 |
1 |
0,0909 |
-0,1883 |
|
|
2 |
0,0909 |
-0,1151 |
|
|
3 |
0,0909 |
-0,0760 |
|
|
4 |
0,0909 |
-0,0471 |
|
|
5 |
0,9099 |
-0,0234 |
|
|
6 |
0,0909 |
0,0000 |
|
|
7 |
0,0909 |
0,0234 |
|
|
8 |
0,0909 |
0,0471 |
|
|
9 |
0,0909 |
0,0760 |
|
|
10 |
0,0909 |
0,1151 |
|
|
11 |
0,0909 |
0,1883 |
|
12 |
1 |
-2,1723 |
-1,9474 |
|
|
2 |
3,1723 |
1,9474 |
|
12 |
1 |
-0,8225 |
-0,0075 |
|
|
2 |
-0,3249 |
-0,4874 |
|
|
3 |
2,1474 |
1,4918 |
|
12 |
1 |
-0,4059 |
-0,6836 |
|
|
2 |
-0,1472 |
-0,3493 |
|
|
3 |
-0,0321 |
-0,1096 |
|
|
4 |
1,5852 |
1,2324 |
|
12 |
1 |
-0,2125 |
-0,5171 |
|
|
2 |
-0,0609 |
-0,2749 |
|
|
3 |
0,0070 |
-0,1659 |
|
|
4 |
0,0589 |
-0,0820 |
|
|
5 |
0,2075 |
1,0399 |
|
12 |
1 |
0,1048 |
-0,4146 |
|
|
2 |
0,0109 |
-0,2274 |
|
|
3 |
0,0313 |
-0,1428 |
|
|
4 |
0,0637 |
-0,0744 |
|
|
5 |
0,0915 |
-0,0210 |
|
|
6 |
0,9292 |
0,8833 |
|
12 |
1 |
-0,0382 |
-0,3448 |
|
|
2 |
0,0210 |
-0,1939 |
|
|
3 |
0,0477 |
-0,1255 |
|
|
4 |
0,0684 |
-0,0726 |
|
|
5 |
0,0861 |
-0,0267 |
|
|
6 |
0,0222 |
0,0155 |
|
|
7 |
0,7128 |
0,7479 |
|
12 |
1 |
0,067 |
-0,2937 |
|
|
2 |
0,0428 |
-0,1686 |
|
|
3 |
0,0585 |
-0,1119 |
|
|
4 |
0,0724 |
-0,0678 |
|
|
5 |
0,0836 |
-0,0298 |
|
|
6 |
0,0938 |
0,0058 |
|
|
7 |
0,1036 |
0,0400 |
|
|
8 |
0,3386 |
0,6259 |
|
12 |
1 |
0,0360 |
-0,2545 |
|
|
2 |
0,0581 |
-0,1487 |
|
|
3 |
0,0682 |
-0,1007 |
|
|
4 |
0,0759 |
-0,0633 |
|
|
5 |
0,0827 |
-0,0308 |
|
|
6 |
0,0888 |
-0,0007 |
|
|
7 |
0,0948 |
0,0286 |
|
|
8 |
0,1006 |
0,0582 |
|
|
9 |
0,3950 |
0,5119 |
|
12 |
1 |
0,0574 |
-0,2232 |
|
|
2 |
0,0693 |
-0,1324 |
|
|
3 |
0,0747 |
-0,0911 |
|
|
4 |
0,0789 |
-0,0590 |
|
|
5 |
0,0825 |
-0,0310 |
|
|
6 |
0,0859 |
-0,0050 |
|
|
7 |
0,0891 |
0,0203 |
|
|
8 |
0,0923 |
0,0461 |
|
|
9 |
0,0959 |
0,0733 |
|
|
10 |
0,2745 |
0,4020 |
|
12 |
1 |
0,0726 |
-0,1972 |
|
|
2 |
0,0775 |
-0,1185 |
|
|
3 |
0,0796 |
-0,0827 |
|
|
4 |
0,0813 |
-0,0548 |
|
|
5 |
0,0828 |
0,0305 |
|
|
6 |
0,0842 |
0,0079 |
|
|
7 |
0,0855 |
0,0142 |
|
|
8 |
0,0868 |
0,0367 |
|
|
9 |
0,0882 |
0,0608 |
|
|
10 |
0,0896 |
0,0881 |
|
|
11 |
0,1789 |
0,2919 |
|
12 |
1 |
0,0833 |
-0,1748 |
|
|
2 |
0,0833 |
-0,1061 |
|
|
3 |
0,0833 |
-0,0749 |
|
|
4 |
0,0833 |
-0,0506 |
|
|
5 |
0,0833 |
-0,0294 |
|
|
6 |
0,0833 |
-0,0297 |
|
|
7 |
0,0833 |
0,0097 |
|
|
8 |
0,0833 |
0,0294 |
|
|
9 |
0,0833 |
0,0506 |
|
|
10 |
0,0833 |
0,0749 |
|
|
11 |
0,0833 |
0,1061 |
|
|
12 |
0,0833 |
0,1748 |
|
13 |
1 |
-2,3101 |
-1,9845 |
|
|
2 |
3,3101 |
1,9845 |
|
13 |
1 |
-0,8916 |
-1,0268 |
|
|
2 |
-0,3753 |
-0,5094 |
|
|
3 |
2,2699 |
1,5360 |
|
13 |
1 |
-0,4561 |
-0,6969 |
|
|
2 |
-0,1817 |
-0,3638 |
|
|
3 |
-0,0610 |
-0,2165 |
|
|
4 |
1,6958 |
1,2773 |
|
13 |
1 |
-0,2516 |
-0,5276 |
|
|
2 |
-0,0876 |
-0,2859 |
|
|
3 |
-0,0151 |
-0,1785 |
|
|
4 |
0,0400 |
-0,0964 |
|
|
5 |
1,3143 |
1,0834 |
|
13 |
1 |
-0,1371 |
-0,4236 |
|
|
2 |
-0,0330 |
-0,2663 |
|
|
3 |
0,0132 |
-0,1528 |
|
|
4 |
0,0484 |
-0,0888 |
|
|
5 |
0,0784 |
-0,0341 |
|
|
6 |
1,0301 |
0,9355 |
|
13 |
1 |
-0,0659 |
-0,3528 |
|
|
2 |
0,0020 |
-0,2015 |
|
|
3 |
0,0322 |
-0,1339 |
|
|
4 |
0,0553 |
-0,0819 |
|
|
5 |
0,0750 |
-0,0374 |
|
|
6 |
0,0923 |
0,0032 |
|
|
7 |
0,8085 |
0,8042 |
|
13 |
1 |
-0,0185 |
-0,3011 |
|
|
2 |
0,0259 |
-0,1754 |
|
|
3 |
0,0457 |
-0,1197 |
|
|
4 |
0,0610 |
-0,0758 |
|
|
5 |
0,0740 |
-0,0386 |
|
|
6 |
0,0857 |
-0,0046 |
|
|
7 |
0,0968 |
0,0276 |
|
|
8 |
0,6294 |
0,6867 |
|
13 |
1 |
0,0144 |
-0,2616 |
|
|
2 |
0,0430 |
-0,1549 |
|
|
3 |
0,0557 |
-0,1071 |
|
|
4 |
0,0655 |
-0,0703 |
|
|
5 |
0,0739 |
-0,0386 |
|
|
6 |
0,0816 |
-0,0095 |
|
|
7 |
0,0888 |
0,0182 |
|
|
8 |
0,0958 |
0,0456 |
|
|
9 |
0,4813 |
0,5781 |
|
13 |
1 |
0,0380 |
-0,2301 |
|
|
2 |
0,0555 |
-0,1382 |
|
|
3 |
0,0633 |
-0,0970 |
|
|
4 |
0,0693 |
-0,0653 |
|
|
5 |
0,0745 |
-0,0379 |
|
|
6 |
0,0792 |
-0,0128 |
|
|
7 |
0,0836 |
0,0113 |
|
|
8 |
0,0880 |
0,0352 |
|
|
9 |
0,0924 |
0,0598 |
|
|
10 |
0,3564 |
0,4750 |
|
13 |
1 |
0,0552 |
-0,2043 |
|
|
2 |
0,0648 |
-0,1243 |
|
|
3 |
0,0691 |
-0,0884 |
|
|
4 |
0,0724 |
-0,0607 |
|
|
5 |
0,0752 |
-0,0368 |
|
|
6 |
0,0778 |
-0,0148 |
|
|
7 |
0,0803 |
0,0063 |
|
|
8 |
0,0827 |
0,0273 |
|
|
9 |
0,0852 |
0,0490 |
|
|
10 |
0,0877 |
0,0723 |
|
|
11 |
0,2497 |
0,3743 |
|
13 |
1 |
0,0679 |
-0,1824 |
|
|
2 |
0,0718 |
-0,1222 |
|
|
3 |
0,0735 |
-0,0806 |
|
|
4 |
0,0749 |
0,0563 |
|
|
5 |
0,0761 |
-0,0353 |
|
|
6 |
0,0771 |
-0,0160 |
|
|
7 |
0,0781 |
0,0026 |
|
|
8 |
0,0792 |
0,0212 |
|
|
9 |
0,0802 |
0,0404 |
|
|
10 |
0,0813 |
0,0612 |
|
|
11 |
0,0824 |
0,0850 |
|
|
12 |
0,1576 |
0,2724 |
|
13 |
1 |
0,0769 |
-0,1632 |
|
|
2 |
0,0769 |
-0,1013 |
|
|
3 |
0,0769 |
-0,0735 |
|
|
4 |
0,0769 |
-0,0520 |
|
|
5 |
0,0769 |
-0,0335 |
|
|
6 |
0,0769 |
-0,0164 |
|
|
7 |
0,0769 |
+0,0164 |
|
|
8 |
0,0769 |
0,0000 |
|
|
9 |
0,0769 |
0,0335 |
|
|
10 |
0,0769 |
0,0164 |
|
|
11 |
0,0769 |
0,0735 |
|
|
12 |
0,0769 |
0,1013 |
|
|
13 |
0,0769 |
0,1632 |
|
14 |
1 |
-2,4378 |
-2,0182 |
|
|
2 |
3,4378 |
2,0182 |
|
14 |
1 |
-0,9616 |
-1,0441 |
|
|
2 |
-0,4228 |
-0,5293 |
|
|
3 |
2,3843 |
1,5734 |
|
14 |
1 |
-0,5027 |
-0,7091 |
|
|
2 |
-0,2142 |
-0,3771 |
|
|
3 |
-0,0866 |
-0,2318 |
|
|
4 |
1,8054 |
1,3180 |
|
14 |
1 |
-0,5027 |
-0,7091 |
|
|
2 |
-0,1127 |
-0,2959 |
|
|
3 |
0,0360 |
-0,1898 |
|
|
4 |
0,0218 |
-0,1094 |
|
|
5 |
1,4148 |
1,1322 |
|
14 |
1 |
-0,1670 |
-0,4317 |
|
|
2 |
-0,0537 |
-0,2444 |
|
|
3 |
-0,0040 |
-0,1618 |
|
|
4 |
0,0388 |
-0,0990 |
|
|
5 |
0,0655 |
-0,0457 |
|
|
6 |
1,1255 |
0,9855 |
|
14 |
1 |
-0,0915 |
-0,3599 |
|
|
2 |
-0,0158 |
-0,2084 |
|
|
3 |
0,017 |
-0,1414 |
|
|
4 |
0,042 |
-0,0903 |
|
|
5 |
0,064 |
-0,0469 |
|
|
6 |
0,083 |
-0,0770 |
|
|
7 |
0,899 |
0,8546 |
|
14 |
1 |
-0,0411 |
-0,3077 |
|
|
2 |
0,0102 |
-0,1815 |
|
|
3 |
0,0328 |
-0,1256 |
|
|
4 |
0,0500 |
-0,0829 |
|
|
5 |
0,0646 |
-0,0466 |
|
|
6 |
0,0777 |
-0,0137 |
|
|
7 |
0,0899 |
0,0172 |
|
|
8 |
0,7159 |
0,7407 |
|
14 |
1 |
-0,0057 |
-0,2678 |
|
|
2 |
0,0288 |
-0,1604 |
|
|
3 |
0,0410 |
-0,1129 |
|
|
4 |
0,0557 |
-0,0765 |
|
|
5 |
0,0655 |
-0,0455 |
|
|
6 |
0,0744 |
-0,0174 |
|
|
7 |
0,0828 |
0,0092 |
|
|
8 |
0,0908 |
0,0350 |
|
|
9 |
0,5637 |
0,6363 |
|
14 |
1 |
0,0199 |
-0,2361 |
|
|
2 |
0,0426 |
-0,1434 |
|
|
3 |
0,0526 |
-0,1023 |
|
|
4 |
0,0602 |
0,0709 |
|
|
5 |
0,0667 |
-0,0440 |
|
|
6 |
0,0726 |
-0,0196 |
|
|
7 |
0,0782 |
0,0035 |
|
|
8 |
0,0835 |
0,0260 |
|
|
9 |
0,0887 |
0,0487 |
|
|
10 |
0,4350 |
0,5382 |
|
14 |
1 |
0,0388 |
-0,2102 |
|
|
2 |
0,0529 |
-0,1292 |
|
|
3 |
0,0592 |
-0,0933 |
|
|
4 |
0,0639 |
-0,0658 |
|
|
5 |
0,0680 |
-0,0423 |
|
|
6 |
0,0717 |
-0,0209 |
|
|
7 |
0,0752 |
-0,0006 |
|
|
8 |
0,0785 |
0,0192 |
|
|
9 |
0,0819 |
0,0393 |
|
|
10 |
0,0852 |
0,0601 |
|
|
11 |
0,3247 |
0,4438 |
|
14 |
1 |
0,0530 |
-0,1885 |
|
|
2 |
0,0609 |
-0,1171 |
|
|
3 |
0,0643 |
-0,0854 |
|
|
4 |
0,0670 |
-0,0612 |
|
|
5 |
0,0692 |
-0,0404 |
|
|
6 |
0,0713 |
-0,0215 |
|
|
7 |
0,0732 |
-0,0036 |
|
|
8 |
0,0751 |
0,0140 |
|
|
9 |
0,0770 |
0,0319 |
|
|
10 |
0,0789 |
0,0505 |
|
|
11 |
0,0809 |
0,0707 |
|
|
12 |
0,2291 |
0,3506 |
|
14 |
1 |
0,0637 |
-0,1698 |
|
|
2 |
0,0669 |
-0,1065 |
|
|
3 |
0,0683 |
-0,0784 |
|
|
4 |
0,0694 |
-0,0568 |
|
|
5 |
0,0704 |
-0,0384 |
|
|
6 |
0,0712 |
-0,0216 |
|
|
7 |
0,0721 |
-0,0056 |
|
|
8 |
0,0728 |
0,0100 |
|
|
9 |
0,0736 |
0,0259 |
|
|
10 |
0,0745 |
0,0426 |
|
|
11 |
0,0753 |
0,0609 |
|
|
12 |
0,0762 |
0,0820 |
|
|
13 |
0,1455 |
0,2556 |
|
14 |
1 |
0,0714 |
-0,1532 |
|
|
2 |
0,0714 |
-0,0968 |
|
|
3 |
0,0714 |
-0,0717 |
|
|
4 |
0,0714 |
-0,0526 |
|
|
5 |
0,0714 |
-0,0362 |
|
|
6 |
0,0714 |
-0,0212 |
|
|
7 |
0,0714 |
-0,0070 |
|
|
8 |
0,0714 |
0,0000 |
|
|
9 |
0,0714 |
0,0212 |
|
|
10 |
0,0714 |
0,0362 |
|
|
11 |
0,0714 |
0,0256 |
|
|
12 |
0,0714 |
0,0717 |
|
|
13 |
0,0714 |
0,0968 |
|
|
14 |
0,0714 |
0,1532 |
|
15 |
1 |
-2,5574 |
-2,0493 |
|
|
2 |
3,5574 |
2,0493 |
|
15 |
1 |
-1,0242 |
-1,0601 |
|
|
2 |
-0,4676 |
-0,5477 |
|
|
3 |
2,4918 |
1,6077 |
|
15 |
1 |
-0,5462 |
-0,7201 |
|
|
2 |
-0,2448 |
-0,3892 |
|
|
3 |
-0,1148 |
-0,2458 |
|
|
4 |
1,9058 |
1,3552 |
|
15 |
1 |
-0,3217 |
-0,5459 |
|
|
2 |
-0,1364 |
-0,3050 |
|
|
3 |
-0,0560 |
-0,2002 |
|
|
4 |
0,0043 |
-0,1211 |
|
|
5 |
1,5097 |
1,1722 |
|
15 |
1 |
-0,1950 |
-0,4390 |
|
|
2 |
-0,0732 |
-0,2518 |
|
|
3 |
-0,0203 |
-0,1700 |
|
|
4 |
0,0196 |
-0,1082 |
|
|
5 |
0,0531 |
-0,0562 |
|
|
6 |
1,2157 |
1,0252 |
|
15 |
1 |
-0,1155 |
-0,3664 |
|
|
2 |
-0,0326 |
-0,2146 |
|
|
3 |
+0,0036 |
-0,1482 |
|
|
4 |
0,0309 |
-0,0979 |
|
|
5 |
0,0539 |
-0,0555 |
|
|
6 |
0,0743 |
-0,0174 |
|
|
7 |
0,9854 |
0,9001 |
|
15 |
1 |
-0,0821 |
-0,3136 |
|
|
2 |
-0,0046 |
-0,1870 |
|
|
3 |
0,0205 |
-0,1315 |
|
|
4 |
0,0395 |
-0,0894 |
|
|
5 |
0,0555 |
-0,0538 |
|
|
6 |
0,0698 |
-0,0219 |
|
|
7 |
0,0830 |
0,0079 |
|
|
8 |
0,7983 |
0,7892 |
|
15 |
1 |
-0,0244 |
-0,2733 |
|
|
2 |
0,0155 |
-0,1654 |
|
|
3 |
0,0330 |
-0,1181 |
|
|
4 |
0,0462 |
-0,0822 |
|
|
5 |
0,0574 |
-0,0518 |
|
|
6 |
0,0674 |
-0,0244 |
|
|
7 |
0,0767 |
0,0012 |
|
|
8 |
0,0856 |
0,0258 |
|
|
9 |
0,6245 |
0,6882 |
|
15 |
1 |
0,0030 |
-0,2414 |
|
|
2 |
0,0305 |
-0,1481 |
|
|
3 |
0,0425 |
-0,1071 |
|
|
4 |
0,0516 |
-0,0760 |
|
|
5 |
0,0593 |
-0,0496 |
|
|
6 |
0,0663 |
-0,0258 |
|
|
7 |
0,0727 |
-0,0035 |
|
|
8 |
0,0789 |
0,0180 |
|
|
9 |
0,0849 |
0,0393 |
|
|
10 |
0,5104 |
0,5940 |
|
15 |
1 |
0,0234 |
-0,2154 |
|
|
2 |
0,0418 |
-0,1336 |
|
|
3 |
0,0498 |
-0,0977 |
|
|
4 |
0,0560 |
-0,0705 |
|
|
5 |
0,0611 |
-0,0473 |
|
|
6 |
0,0658 |
-0,0264 |
|
|
7 |
0,0701 |
-0,0068 |
|
|
8 |
0,0743 |
0,0122 |
|
|
9 |
0,0784 |
0,0310 |
|
|
10 |
0,0824 |
0,0502 |
|
|
11 |
0,3669 |
0,5042 |
|
15 |
1 |
0,0390 |
-0,1937 |
|
|
2 |
0,0506 |
-0,1214 |
|
|
3 |
0,0556 |
-0,0897 |
|
|
4 |
0,0595 |
-0,0655 |
|
|
5 |
0,0628 |
-0,0450 |
|
|
6 |
0,0657 |
-0,0265 |
|
|
7 |
0,0685 |
-0,0091 |
|
|
8 |
0,0711 |
0,0078 |
|
|
9 |
0,0737 |
0,0246 |
|
|
10 |
0,0763 |
0,0417 |
|
|
11 |
0,0790 |
0,0598 |
|
|
12 |
0,2982 |
0,4169 |
|
15 |
1 |
0,0508 |
-0,1752 |
|
|
2 |
0,0574 |
-0,1108 |
|
|
3 |
0,0602 |
-0,0825 |
|
|
4 |
0,0624 |
-0,0610 |
|
|
5 |
0,0642 |
-0,0427 |
|
|
6 |
0,0659 |
-0,0262 |
|
|
7 |
0,0675 |
-0,0106 |
|
|
8 |
0,0690 |
0,0044 |
|
|
9 |
0,0704 |
0,0195 |
|
|
10 |
0,0719 |
0,0349 |
|
|
11 |
0,0735 |
0,0512 |
|
|
12 |
0,0751 |
0,0690 |
|
|
13 |
0,2216 |
0,3300 |
|
15 |
1 |
0,0599 |
-0,1590 |
|
|
2 |
0,0627 |
-0,1013 |
|
|
3 |
0,0639 |
-0,0760 |
|
|
4 |
0,0648 |
-0,0568 |
|
|
5 |
0,0655 |
-0,0404 |
|
|
6 |
0,0662 |
-0,0256 |
|
|
7 |
0,0669 |
-0,1116 |
|
|
8 |
0,0675 |
0,0019 |
|
|
9 |
0,0682 |
0,0154 |
|
|
10 |
0,0688 |
0,0293 |
|
|
11 |
0,0695 |
0,0440 |
|
|
12 |
0,0702 |
0,0602 |
|
|
13 |
0,0709 |
0,0791 |
|
|
14 |
0,1351 |
0,2409 |
|
15 |
1 |
0,0667 |
-0,1444 |
|
|
2 |
0,0667 |
-0,0927 |
|
|
3 |
0,0667 |
-0,0699 |
|
|
4 |
0,0667 |
-0,0526 |
|
|
5 |
0,0667 |
-0,0379 |
|
|
6 |
0,0667 |
-0,0247 |
|
|
7 |
0,0667 |
-0,0122 |
|
|
8 |
0,0667 |
0,0000 |
|
|
9 |
0,0667 |
0,0122 |
|
|
10 |
0,0667 |
0,0247 |
|
|
11 |
0,0667 |
0,0379 |
|
|
12 |
0,0667 |
0,0526 |
|
|
13 |
0,0667 |
0,0699 |
|
|
14 |
0,0667 |
0,0927 |
|
|
15 |
0,0667 |
0,1444 |
Таблица 65
|
|
|
| ||||||||
|
|
|
0,05 |
0,10 |
0,25 |
0,40 |
0,50 |
0,60 |
0,75 |
0,90 |
0,95 |
|
3 |
3 |
-2,54 |
-1,49 |
-0,52 |
-0,10 |
0,10 |
0,31 |
0,69 |
1,46 |
2,12 |
|
4 |
3 |
-3,85 |
-2,32 |
-0,84 |
-0,29 |
-0,04 |
0,18 |
0,50 |
1,06 |
1,55 |
|
|
4 |
-1,50 |
-0,96 |
-0,37 |
-0,08 |
0,09 |
0,25 |
0,55 |
1,07 |
1,49 |
|
5 |
3 |
-5,22 |
-3,04 |
-1,22 |
-0,50 |
-0,19 |
0,06 |
0,40 |
0,86 |
1,20 |
|
|
4 |
-1,94 |
-1,24 |
-0,50 |
-0,16 |
0,02 |
0,18 |
0,45 |
0,88 |
1,22 |
|
|
5 |
-1,08 |
-0,73 |
-0,31 |
-0,06 |
0,08 |
0,22 |
0,47 |
0,89 |
1,20 |
|
6 |
3 |
-6,12 |
-3,72 |
-1,56 |
-0,69 |
-0,32 |
-0,04 |
0,33 |
0,75 |
1,02 |
|
|
4 |
-2,39 |
-1,59 |
-0,67 |
-0,25 |
-0,05 |
0,12 |
0,38 |
0,76 |
1,03 |
|
|
5 |
-1,36 |
-0,91 |
-0,38 |
-0,11 |
0,04 |
0,17 |
0,40 |
0,77 |
1,04 |
|
|
6 |
-0,91 |
-0,64 |
-0,28 |
-0,06 |
0,07 |
0,19 |
0,41 |
0,77 |
1,04 |
|
7 |
3 |
-7,39 |
-4,45 |
-1,87 |
-0,89 |
-0,48 |
-0,16 |
0,26 |
0,68 |
0,90 |
|
|
4 |
-2,95 |
-1,94 |
-0,84 |
-0,36 |
-0,13 |
0,05 |
0,32 |
0,66 |
0,89 |
|
|
5 |
-1,59 |
-1,10 |
-0,48 |
-0,17 |
-0,02 |
0,12 |
0,34 |
0,66 |
0,89 |
|
|
6 |
-1,04 |
-0,73 |
-0,32 |
-0,10 |
0,03 |
0,15 |
0,35 |
0,67 |
0,90 |
|
|
7 |
-0,79 |
-0,56 |
-0,26 |
-0,06 |
0,05 |
0,17 |
0,36 |
0,68 |
0,90 |
|
8 |
3 |
-8,15 |
-5,01 |
-2,14 |
-1,04 |
-0,58 |
-0,21 |
0,24 |
0,67 |
0,88 |
|
|
4 |
-3,30 |
-2,18 |
-0,99 |
-0,43 |
-0,19 |
0,02 |
0,30 |
0,64 |
0,83 |
|
|
5 |
-1,86 |
-1,25 |
-0,56 |
-0,22 |
-0,05 |
0,10 |
0,32 |
0,62 |
0,82 |
|
|
6 |
-1,20 |
-0,83 |
-0,36 |
-0,12 |
0,01 |
0,13 |
0,33 |
0,63 |
0,82 |
|
|
7 |
-0,88 |
-0,61 |
-0,27 |
-0,07 |
0,04 |
0,15 |
0,33 |
0,63 |
0,82 |
|
|
8 |
-0,70 |
-0,50 |
-0,22 |
-0,05 |
0,06 |
0,16 |
0,34 |
0,63 |
0,82 |
|
9 |
3 |
-9,12 |
-5,64 |
-2,38 |
-1,17 |
-0,66 |
-0,28 |
0,20 |
0,66 |
0,86 |
|
|
4 |
-3,78 |
-2,47 |
-1,08 |
-0,50 |
-0,24 |
-0,01 |
0,28 |
0,61 |
0,79 |
|
|
5 |
-2,10 |
-1,40 |
-0,63 |
-0,26 |
-0,08 |
0,08 |
0,30 |
0,58 |
0,76 |
|
|
6 |
-1,38 |
-0,94 |
-0,41 |
-0,15 |
-0,01 |
0,11 |
0,30 |
0,57 |
0,76 |
|
|
7 |
-0,99 |
-0,70 |
-0,31 |
-0,10 |
0,02 |
0,13 |
0,31 |
0,57 |
0,76 |
|
|
8 |
-0,76 |
-0,55 |
-0,25 |
-0,07 |
0,04 |
0,14 |
0,31 |
0,58 |
0,76 |
|
|
9 |
-0,64 |
-0,47 |
-0,21 |
-0,05 |
0,05 |
0,15 |
0,32 |
0,58 |
0,76 |
|
10 |
3 |
-9,98 |
-6,05 |
-2,58 |
-1,29 |
-0,76 |
-0,34 |
0,17 |
0,66 |
0,87 |
|
|
4 |
-4,17 |
-2,70 |
-1,22 |
-0,58 |
-0,28 |
-0,04 |
0,27 |
0,60 |
0,77 |
|
|
5 |
-2,37 |
-1,56 |
-0,73 |
-0,31 |
-0,12 |
0,05 |
0,28 |
0,56 |
0,72 |
|
|
6 |
-1,51 |
-1,03 |
-0,48 |
-0,19 |
-0,04 |
0,09 |
0,28 |
0,54 |
0,71 |
|
|
7 |
-1,08 |
-0,77 |
-0,35 |
-0,12 |
-0,00 |
0,11 |
0,28 |
0,54 |
0,70 |
|
|
8 |
-0,86 |
-0,62 |
-0,27 |
-0,08 |
0,02 |
0,12 |
0,28 |
0,53 |
0,71 |
|
|
9 |
-0,70 |
-0,50 |
-0,23 |
-0,06 |
0,04 |
0,13 |
0,29 |
0,54 |
0,71 |
|
|
10 |
-0,60 |
-0,44 |
-0,20 |
-0,04 |
0,04 |
0,14 |
0,29 |
0,54 |
0,71 |
|
11 |
3 |
-10,68 |
-6,42 |
-2,76 |
-1,41 |
-0,85 |
-0,42 |
0,13 |
0,65 |
0,87 |
|
|
4 |
-4,57 |
-2,95 |
-1,37 |
-0,66 |
-0,36 |
-0,10 |
0,24 |
0,58 |
0,75 |
|
|
5 |
-2,58 |
-1,75 |
-0,81 |
-0,37 |
-0,16 |
0,01 |
0,26 |
0,54 |
0,69 |
|
|
6 |
-1,67 |
-1,16 |
-0,53 |
-0,22 |
-0,07 |
0,06 |
0,26 |
0,52 |
0,66 |
|
|
7 |
-1,21 |
-0,85 |
-0,40 |
-0,15 |
-0,02 |
0,09 |
0,26 |
0,50 |
0,65 |
|
|
8 |
-0,92 |
-0,66 |
-0,30 |
-0,11 |
0,00 |
0,10 |
0,26 |
0,50 |
0,65 |
|
|
9 |
-0,76 |
-0,54 |
-0,25 |
-0,08 |
0,02 |
0,11 |
0,26 |
0,50 |
0,65 |
|
|
10 |
-0,63 |
-0,46 |
-0,21 |
-0,06 |
0,03 |
0,12 |
0,27 |
0,50 |
0,65 |
|
|
11 |
-0,55 |
-0,42 |
-0,19 |
-0,05 |
0,03 |
0,12 |
0,27 |
0,50 |
0,65 |
|
12 |
3 |
-11,32 |
-6,92 |
-3,03 |
-1,58 |
-0,97 |
-0,49 |
0,10 |
0,64 |
0,88 |
|
|
4 |
-4,81 |
-3,17 |
-1,47 |
-0,74 |
-0,40 |
-0,14 |
0,21 |
0,58 |
0,75 |
|
|
5 |
-2,72 |
-1,88 |
-0,89 |
-0,42 |
-0,20 |
-0,01 |
0,24 |
0,53 |
0,68 |
|
|
6 |
-1,83 |
-1,27 |
-0,60 |
-0,26 |
-0,10 |
0,05 |
0,25 |
0,50 |
0,64 |
|
|
7 |
-1,32 |
-0,92 |
-0,42 |
-0,17 |
-0,04 |
0,08 |
0,25 |
0,48 |
0,62 |
|
|
8 |
-1,00 |
-0,71 |
-0,33 |
-0,12 |
-0,01 |
0,09 |
0,25 |
0,48 |
0,62 |
|
|
9 |
-0,80 |
-0,58 |
-0,27 |
-0,09 |
0,01 |
0,10 |
0,25 |
0,47 |
0,62 |
|
|
10 |
-0,67 |
-0,48 |
-0,23 |
-0,07 |
0,02 |
0,11 |
0,25 |
0,47 |
0,62 |
|
|
11 |
-0,58 |
-0,43 |
-0,20 |
-0,06 |
0,03 |
0,11 |
0,25 |
0,47 |
0,62 |
|
|
12 |
-0,53 |
-0,39 |
-0,19 |
-0,05 |
0,03 |
0,11 |
0,25 |
0,47 |
0,62 |
|
13 |
3 |
-11,66 |
-7,41 |
-3,21 |
-1,64 |
-1,02 |
-0,54 |
0,08 |
0,65 |
0,88 |
|
|
4 |
-5,21 |
-3,37 |
-1,60 |
-0,82 |
-0,48 |
-0,19 |
0,20 |
0,59 |
0,76 |
|
|
5 |
-2,95 |
-1,99 |
-0,96 |
-0,47 |
-0,24 |
-0,04 |
0,24 |
0,54 |
0,68 |
|
|
6 |
-1,94 |
-1,35 |
-0,66 |
-0,31 |
-0,13 |
0,03 |
0,25 |
0,51 |
0,64 |
|
|
7 |
-1,40 |
-0,98 |
-0,46 |
-0,19 |
-0,06 |
0,06 |
0,25 |
0,47 |
0,61 |
|
|
8 |
-1,06 |
-0,77 |
-0,36 |
-0,14 |
-0,02 |
0,08 |
0,24 |
0,46 |
0,59 |
|
|
9 |
-0,86 |
-0,61 |
-0,29 |
-0,10 |
-0,00 |
0,09 |
0,24 |
0,45 |
0,58 |
|
|
10 |
-0,72 |
-0,52 |
-0,24 |
-0,08 |
0,01 |
0,10 |
0,24 |
0,45 |
0,58 |
|
|
11 |
-0,63 |
-0,45 |
-0,21 |
-0,06 |
0,02 |
0,11 |
0,24 |
0,45 |
0,58 |
|
|
12 |
-0,56 |
-0,41 |
-0,19 |
-0,05 |
0,03 |
0,11 |
0,25 |
0,45 |
0,59 |
|
|
13 |
-0,51 |
-0,38 |
-0,18 |
-0,05 |
0,04 |
0,11 |
0,25 |
0,45 |
0,59 |
|
14 |
3 |
-12,49 |
-7,65 |
-3,31 |
-1,71 |
-1,08 |
-0,57 |
0,06 |
0,65 |
0,90 |
|
|
4 |
-5,38 |
-3,53 |
-1,68 |
-0,87 |
-0,49 |
-0,20 |
0,19 |
0,59 |
0,77 |
|
|
5 |
-3,13 |
-2,17 |
-1,03 |
-0,51 |
-0,26 |
-0,04 |
0,24 |
0,54 |
0,69 |
|
|
6 |
-2,10 |
-1,45 |
-0,70 |
-0,32 |
-0,14 |
0,02 |
0,24 |
0,50 |
0,63 |
|
|
7 |
-1,50 |
-1,06 |
-0,50 |
-0,22 |
-0,07 |
0,06 |
0,24 |
0,47 |
0,60 |
|
|
8 |
-1,15 |
-0,81 |
-0,39 |
-0,15 |
-0,04 |
0,08 |
0,24 |
0,45 |
0,58 |
|
|
9 |
-0,93 |
-0,66 |
-0,30 |
-0,11 |
-0,01 |
0,09 |
0,23 |
0,44 |
0,56 |
|
|
10 |
-0,76 |
-0,54 |
-0,26 |
-0,09 |
0,00 |
0,09 |
0,23 |
0,43 |
0,56 |
|
|
11 |
-0,65 |
-0,48 |
-0,22 |
-0,07 |
0,01 |
0,09 |
0,23 |
0,43 |
0,56 |
|
|
12 |
-0,57 |
-0,42 |
-0,19 |
-0,06 |
0,02 |
0,10 |
0,23 |
0,43 |
0,56 |
|
|
13 |
-0,51 |
-0,38 |
-0,18 |
-0,05 |
0,02 |
0,10 |
0,23 |
0,43 |
0,56 |
|
|
14 |
-0,47 |
-0,36 |
-0,17 |
-0,05 |
0,03 |
0,10 |
0,23 |
0,43 |
0,56 |
|
15 |
3 |
-13,14 |
-8,14 |
-3,63 |
-1,92 |
-1,20 |
-0,05 |
0,02 |
0,64 |
0,89 |
|
|
4 |
-5,55 |
-3,74 |
-1,78 |
-0,94 |
-0,55 |
-0,23 |
0,19 |
0,60 |
0,78 |
|
|
5 |
-3,35 |
-2,27 |
-1,10 |
-0,56 |
-0,29 |
-0,07 |
0,23 |
0,55 |
0,70 |
|
|
6 |
-2,21 |
-1,55 |
-0,75 |
-0,36 |
-0,17 |
-0,00 |
0,23 |
0,50 |
0,64 |
|
|
7 |
-1,56 |
-1,11 |
-0,55 |
-0,25 |
-0,09 |
0,04 |
0,23 |
0,47 |
0,59 |
|
|
8 |
-1,20 |
-0,86 |
-0,42 |
-0,18 |
-0,05 |
0,06 |
0,23 |
0,45 |
0,57 |
|
|
9 |
-0,96 |
-0,70 |
-0,35 |
-0,13 |
-0,03 |
0,07 |
0,23 |
0,43 |
0,56 |
|
|
10 |
-0,82 |
-0,59 |
-0,28 |
-0,10 |
-0,01 |
0,08 |
0,23 |
0,42 |
0,55 |
|
|
11 |
-0,70 |
-0,51 |
-0,24 |
-0,08 |
0,01 |
0,09 |
0,23 |
0,42 |
0,54 |
|
|
12 |
-0,62 |
-0,45 |
-0,21 |
-0,07 |
0,01 |
0,09 |
0,23 |
0,41 |
0,54 |
|
|
13 |
-0,55 |
-0,41 |
-0,19 |
-0,06 |
0,02 |
0,10 |
0,23 |
0,41 |
0,54 |
|
|
14 |
-0,50 |
-0,37 |
-0,18 |
-0,05 |
0,03 |
0,10 |
0,22 |
0,41 |
0,54 |
|
|
15 |
-0,46 |
-0,35 |
-0,17 |
-0,04 |
0,03 |
0,10 |
0,23 |
0,42 |
0,54 |
Таблица 66
|
|
|
|
|
0,80 |
1,61 |
0,842 |
|
0,90 |
2,30 |
1,282 |
|
0,95 |
3,00 |
1,645 |
|
0,975 |
3,69 |
1,960 |
|
0,990 |
4,61 |
2,326 |
|
0,995 |
5,30 |
2,576 |
|
0,9975 |
6,00 |
2,807 |
|
0,999 |
6,91 |
3,090 |
Таблица 67
|
|
|
|
1 |
1,253 |
|
2 |
1,128 |
|
3 |
1,085 |
|
4 |
1,064 |
|
5 |
1,051 |
|
6 |
1,042 |
|
7 |
1,036 |
|
8 |
1,032 |
|
9 |
1,028 |
|
10 |
1,025 |
|
11 |
1,023 |
|
12 |
1,021 |
|
13 |
1,019 |
|
14 |
1,018 |
|
15 |
1,017 |
|
16 |
1,016 |
|
17 |
1,015 |
|
18 |
1,014 |
|
19 |
1,013 |
|
20 |
1,013 |
|
25 |
1,010 |
|
30 |
1,008 |
|
35 |
1,007 |
|
40 |
1,006 |
|
45 |
1,006 |
|
50 |
1,005 |
|
60 |
1,004 |
Примечание. Коэффициенты 
для 20<
<60, не указанные в таблице, определяют по табличным значениям с помощью линейной интерполяции.
Таблица 68
|
|
| ||||||||||||
|
|
0,01 |
0,05 |
0,10 |
0,20 |
0,30 |
0,40 |
0,50 |
0,60 |
0,70 |
0,80 |
0,90 |
0,96 |
0,99 |
|
2 |
0,023 |
0,102 |
0,21 |
0,445 |
0,711 |
1,023 |
1,383 |
1,836 |
2,414 |
3,227 |
4,602 |
5,992 |
9,211 |
|
4 |
0,305 |
0,711 |
1,04 |
1,643 |
2,195 |
2,758 |
3,352 |
4,039 |
4,883 |
5,992 |
7,773 |
9,492 |
13,273 |
|
6 |
0,872 |
1,635 |
2,204 |
3,064 |
3,826 |
4,564 |
5,350 |
6,205 |
7,236 |
8,561 |
10,645 |
12,592 |
16,812 |
|
8 |
1,646 |
2,733 |
3,490 |
4,586 |
5,523 |
6,430 |
7,352 |
8,352 |
9,523 |
11,023 |
15,362 |
13,507 |
20,090 |
|
10 |
2,558 |
3,940 |
4,865 |
6,182 |
7,275 |
8,291 |
9,346 |
10,479 |
11,787 |
13,447 |
15,987 |
18,307 |
23,209 |
|
12 |
3,571 |
5,226 |
6,304 |
7,811 |
9,029 |
10,178 |
11,338 |
12,580 |
14,010 |
15,814 |
18,549 |
21,026 |
26,217 |
|
14 |
4,660 |
6,571 |
7,790 |
9,468 |
10,821 |
12,079 |
13,337 |
14,690 |
16,222 |
18,149 |
21,064 |
23,685 |
29,141 |
|
16 |
5,812 |
7,962 |
9,312 |
11,148 |
12,617 |
13,977 |
16,336 |
16,773 |
18,414 |
20,461 |
23,542 |
26,296 |
32,000 |
|
18 |
7,015 |
9,390 |
10,868 |
12,858 |
14,440 |
15,899 |
17,341 |
18,870 |
20,593 |
22,755 |
25,939 |
28,869 |
34,805 |
|
20 |
8,260 |
10,851 |
12,443 |
14,580 |
16,260 |
17,803 |
19,436 |
20,947 |
22,763 |
25,029 |
28,412 |
31,410 |
37,566 |
|
22 |
9,542 |
12,338 |
14,041 |
16,312 |
18,106 |
19,728 |
21,339 |
23,026 |
24,938 |
27,301 |
30,813 |
33,924 |
40,289 |
|
24 |
10,856 |
13,848 |
15,659 |
18,064 |
19,939 |
21,650 |
23,338 |
25,107 |
27,100 |
29,549 |
33,196 |
36,415 |
42,980 |
|
26 |
12,198 |
15,379 |
17,292 |
19,824 |
21,792 |
23,582 |
25,333 |
27,174 |
29,244 |
31,795 |
35,563 |
38,885 |
45,042 |
|
28 |
13,565 |
16,928 |
18,939 |
21,595 |
23,646 |
25,505 |
27,337 |
29,251 |
31,397 |
34,022 |
37,916 |
41,337 |
48,278 |
|
30 |
14,953 |
18,493 |
20,599 |
23,357 |
25,510 |
27,444 |
29,333 |
31,311 |
33,523 |
36,248 |
40,256 |
43,773 |
50,892 |
|
32 |
16,362 |
20,072 |
21,271 |
25,148 |
27,367 |
29,383 |
31,336 |
33,383 |
35,664 |
38,461 |
42,585 |
46,194 |
53,486 |
|
34 |
17,789 |
21,664 |
23,952 |
26,936 |
29,244 |
31,319 |
33,328 |
35,436 |
37,793 |
40,682 |
44,903 |
48,602 |
56,061 |
|
36 |
19,233 |
23,269 |
25,643 |
28,731 |
31,122 |
33,249 |
35,311 |
37,503 |
39,929 |
42,582 |
47,212 |
50,998 |
58,619 |
|
38 |
20,691 |
24,884 |
27,343 |
30,537 |
33,000 |
35,189 |
37,341 |
39,568 |
42,036 |
45,079 |
49,513 |
53,384 |
61,162 |
|
40 |
22,164 |
26,509 |
29,051 |
32,354 |
34,873 |
37,139 |
39,326 |
41,631 |
44,170 |
47,275 |
51,805 |
55,758 |
63,691 |
|
42 |
23,650 |
28,144 |
30,765 |
34,161 |
36,755 |
39,073 |
41,339 |
43,677 |
46,181 |
49,460 |
54,090 |
58,124 |
66,206 |
|
44 |
25,148 |
29,787 |
32,487 |
35,970 |
38,645 |
41,019 |
43,339 |
45,735 |
48,399 |
51,643 |
56,369 |
60,481 |
68,710 |
|
46 |
26,657 |
31,439 |
34,215 |
37,796 |
40,525 |
42,973 |
45,332 |
47,791 |
50,509 |
52,822 |
58,641 |
62,830 |
71,201 |
|
48 |
28,177 |
33,098 |
35,949 |
39,615 |
42,416 |
44,912 |
46,338 |
49,846 |
52,611 |
55,998 |
60,907 |
65,171 |
74,683 |
|
50 |
29,707 |
34,764 |
37,689 |
41,449 |
44,318 |
46,869 |
49,335 |
51,886 |
54,718 |
58,160 |
63,167 |
67,505 |
76,154 |
|
52 |
31,246 |
36,437 |
39,433 |
43,285 |
46,205 |
48,807 |
51,333 |
53,936 |
56,831 |
60,334 |
65,422 |
69,832 |
78,616 |
|
54 |
31,793 |
38,116 |
41,183 |
45,121 |
48,100 |
50,763 |
53,334 |
55,997 |
58,924 |
62,497 |
67,673 |
72,153 |
61,069 |
|
56 |
34,350 |
39,801 |
42,937 |
46,956 |
50,005 |
52,712 |
55,337 |
58,014 |
61,024 |
64,661 |
69,919 |
74,468 |
83,513 |
|
58 |
35,913 |
41,492 |
44,696 |
48,801 |
51,904 |
54,665 |
57,342 |
60,089 |
63,133 |
66,815 |
72,160 |
76,778 |
85,950 |
|
60 |
37,485 |
43,188 |
46,459 |
50,647 |
53,811 |
56,246 |
59,333 |
62,131 |
65,222 |
68,972 |
74,397 |
79,082 |
88,379 |
|
62 |
39,063 |
44,899 |
48,226 |
52,487 |
55,711 |
58,572 |
61,342 |
64,187 |
67,321 |
71,120 |
76,630 |
81,381 |
80,802 |
|
64 |
40,649 |
46,595 |
49,996 |
54,336 |
57,617 |
60,523 |
63,336 |
66,227 |
69,414 |
73,273 |
78,860 |
83,675 |
93,217 |
|
66 |
42,240 |
48,305 |
51,770 |
56,195 |
59,531 |
62,479 |
65,331 |
68,264 |
71,503 |
75,418 |
81,085 |
85,965 |
95,626 |
|
68 |
43,858 |
50,020 |
53,548 |
58,047 |
61,434 |
64,438 |
67,438 |
70,316 |
73,803 |
77,571 |
83,803 |
88,250 |
95,028 |
|
70 |
45,442 |
61,739 |
55,329 |
59,891 |
63,344 |
66,403 |
69,342 |
72,350 |
75,682 |
79,716 |
85,527 |
90,531 |
100,43 |
|
72 |
47,051 |
53,462 |
57,113 |
61,761 |
65,259 |
68,353 |
71,341 |
74,399 |
77,774 |
81,853 |
87,743 |
92,808 |
102,82 |
|
74 |
48,666 |
55,189 |
88,900 |
63,621 |
67,162 |
70,305 |
70,305 |
73,341 |
76,448 |
79,863 |
84,000 |
89,956 |
105,20 |
|
76 |
50,286 |
56,920 |
60,690 |
65,470 |
69,088 |
72,261 |
75,341 |
78,477 |
81,947 |
88,140 |
92,166 |
97,351 |
107,58 |
|
78 |
51,910 |
58,654 |
62,483 |
67,345 |
71,002 |
74,220 |
77,343 |
80,523 |
84,027 |
88,274 |
94,374 |
99,617 |
109,98 |
|
80 |
53,540 |
60,391 |
64,278 |
69,209 |
72,920 |
76,182 |
79,326 |
82,568 |
86,153 |
90,400 |
96,578 |
101,88 |
112,33 |
|
82 |
55,174 |
62,132 |
66,076 |
71,074 |
74,828 |
78,151 |
81,334 |
84,808 |
88,201 |
82,535 |
98,780 |
104,14 |
114,70 |
|
84 |
56,813 |
63,876 |
67,876 |
72,941 |
76,756 |
80,109 |
83,339 |
86,651 |
90,281 |
94,663 |
100,98 |
106,40 |
117,06 |
|
86 |
58,456 |
85,723 |
69,679 |
74,814 |
78,667 |
82,068 |
85,333 |
88,682 |
92,367 |
96,797 |
103,18 |
108,65 |
119,41 |
|
88 |
60,103 |
67,373 |
71,484 |
76,683 |
80,593 |
84,031 |
87,339 |
90,723 |
94,440 |
98,930 |
105,37 |
110,90 |
121,77 |
|
90 |
61,754 |
69,126 |
73,291 |
78,558 |
82,513 |
85,995 |
89,335 |
92,763 |
96,520 |
101,06 |
107,57 |
113,15 |
124,12 |
|
92 |
63,409 |
70,882 |
75,100 |
80,438 |
84,436 |
87,951 |
91,332 |
94,802 |
98,598 |
103,18 |
109,76 |
115,39 |
126,46 |
|
94 |
65,068 |
72,640 |
76,912 |
82,313 |
86,352 |
89,921 |
93,329 |
96,840 |
100,68 |
105,31 |
111,94 |
117,63 |
128,80 |
|
96 |
66,730 |
74,701 |
78,725 |
84,182 |
88,283 |
91,881 |
95,338 |
98,877 |
102,76 |
107,42 |
114,13 |
119,87 |
131,14 |
|
98 |
68,396 |
76,164 |
80,541 |
86,067 |
90,206 |
93,843 |
97,336 |
100,91 |
104,82 |
109,55 |
116,32 |
122,11 |
133,48 |
|
100 |
70,065 |
77,929 |
82,358 |
87,946 |
92,133 |
95,807 |
99,335 |
102,95 |
106,90 |
111,66 |
118,50 |
124,34 |
135,81 |
|
110 |
78,458 |
86,792 |
91,471 |
97,358 |
101,76 |
105,63 |
109,33 |
113,12 |
122,25 |
117,27 |
129,39 |
135,48 |
147,41 |
|
120 |
86,923 |
95,705 |
100,62 |
106,81 |
111,42 |
115,47 |
119,33 |
127,61 |
132,81 |
140,23 |
146,57 |
158,95 |
146,57 |
|
130 |
95,451 |
101,66 |
109,81 |
116,26 |
121,09 |
125,31 |
129,34 |
133,45 |
137,94 |
151,05 |
143,34 |
157,61 |
170,42 |
|
140 |
104,03 |
113,66 |
119,03 |
125,76 |
130,76 |
135,14 |
139,32 |
143,60 |
148,26 |
153,85 |
161,83 |
168,61 |
181,84 |
|
150 |
112,67 |
122,69 |
128,28 |
135,21 |
140,45 |
144,09 |
149,34 |
153,74 |
158,58 |
164,35 |
172,58 |
179,58 |
193,21 |
|
200 |
156,43 |
168,28 |
174,84 |
183,00 |
189,04 |
194,32 |
199,33 |
204,42 |
209,98 |
216,58 |
226,02 |
233,90 |
249,45 |
|
300 |
245,97 |
260,88 |
260,07 |
279,21 |
288,68 |
293,18 |
299,33 |
305,57 |
512,33 |
320,39 |
331,79 |
341,40 |
359,91 |
|
400 |
337,16 |
354,64 |
364,21 |
376,02 |
384,70 |
392,22 |
399,33 |
406,52 |
414,32 |
423,58 |
436,65 |
447,63 |
468,72 |
|
500 |
429,39 |
449,15 |
459,93 |
472,21 |
482,95 |
491,37 |
499,34 |
507,38 |
516,09 |
526,40 |
540,93 |
553,13 |
576,49 |
|
600 |
522,36 |
544,18 |
556,06 |
570,68 |
581,35 |
590,60 |
599,33 |
608,14 |
617,66 |
628,92 |
644,80 |
658,09 |
683,52 |
|
800 |
709,90 |
735,35 |
749,49 |
766,16 |
778,55 |
789,25 |
799,33 |
809,50 |
820,48 |
833,45 |
851,67 |
766,91 |
895,98 |
|
1000 |
698,91 |
927,59 |
943,13 |
962,17 |
976,07 |
988,04 |
999,32 |
1010,7 |
1022,9 |
1037,4 |
1057,7 |
1074,7 |
1107,0 |
при
Таблица 69
|
|
|
| |||||
|
|
|
0,05 |
0,10 |
0,25 |
0,90 |
0,95 |
0,98 |
|
3 |
3 |
1,10 |
1,43 |
2,18 |
8,99 |
13,16 |
20,93 |
|
4 |
3 |
1,16 |
1,49 |
2,18 |
9,03 |
13,07 |
20,23 |
|
|
4 |
1,16 |
1,46 |
2,06 |
6,47 |
8,39 |
11,66 |
|
5 |
3 |
1,18 |
1,51 |
2,17 |
8,78 |
12,58 |
20,38 |
|
|
4 |
1,23 |
1,51 |
2,09 |
6,49 |
8,48 |
11,73 |
|
|
5 |
1,23 |
1,49 |
2,02 |
5,48 |
6,73 |
8,66 |
|
6 |
3 |
1,18 |
1,53 |
2,15 |
8,24 |
11,74 |
18,65 |
|
|
4 |
1,28 |
1,55 |
2,10 |
6,33 |
8,18 |
11,39 |
|
|
5 |
1,29 |
1,54 |
2,05 |
5,42 |
6,73 |
8,89 |
|
|
6 |
1,27 |
1,53 |
2,01 |
4,86 |
5,83 |
7,31 |
|
7 |
3 |
1,18 |
1,53 |
2,13 |
7,80 |
11,12 |
17,54 |
|
|
4 |
1,31 |
1,58 |
2,10 |
6,16 |
7,89 |
10,90 |
|
|
5 |
1,33 |
1,57 |
2,06 |
5,36 |
6,68 |
8,44 |
|
|
6 |
1,32 |
1,56 |
2,03 |
4,86 |
5,82 |
7,23 |
|
|
7 |
1,32 |
1,55 |
2,00 |
4,46 |
5,25 |
6,37 |
|
8 |
3 |
1,13 |
1,52 |
2,11 |
7,51 |
10,67 |
16,36 |
|
|
4 |
1,33 |
1,60 |
2,10 |
5,96 |
7,79 |
10,76 |
|
|
5 |
1,36 |
1,60 |
2,08 |
5,28 |
6,50 |
8,62 |
|
|
6 |
1,36 |
1,59 |
2,05 |
4,83 |
5,83 |
7,18 |
|
|
7 |
1,36 |
1,58 |
2,03 |
4,49 |
5,31 |
6,40 |
|
|
8 |
1,36 |
1,58 |
2,01 |
4,21 |
4,90 |
5,84 |
|
9 |
3 |
1,12 |
1,51 |
2,09 |
7,14 |
10,21 |
15,61 |
|
|
4 |
1,36 |
1,61 |
2,10 |
5,77 |
7,39 |
10,26 |
|
|
5 |
1,41 |
1,63 |
2,08 |
5,13 |
6,34 |
8,13 |
|
|
6 |
1,41 |
1,62 |
2,06 |
4,74 |
5,67 |
7,06 |
|
|
7 |
1,41 |
1,62 |
2,04 |
4,48 |
5,28 |
6,46 |
|
|
8 |
1,40 |
1,61 |
2,02 |
4,26 |
4,95 |
5,94 |
|
|
9 |
1,40 |
1,60 |
2,00 |
4,04 |
4,66 |
5,50 |
|
10 |
3 |
0,99 |
1,46 |
2,05 |
6,75 |
9,36 |
14,88 |
|
|
4 |
1,34 |
1,62 |
2,08 |
5,56 |
7,17 |
9,60 |
|
|
5 |
1,42 |
1,64 |
2,07 |
5,00 |
6,13 |
8,02 |
|
|
6 |
1,43 |
1,64 |
2,05 |
4,67 |
5,59 |
6,99 |
|
|
7 |
1,43 |
1,64 |
2,04 |
4,41 |
5,18 |
6,29 |
|
|
8 |
1,43 |
1,63 |
2,02 |
4,22 |
4,91 |
5,83 |
|
|
9 |
1,42 |
1,63 |
2,01 |
4,03 |
4,63 |
5,51 |
|
|
10 |
1,42 |
1,62 |
1,99 |
3,86 |
4,41 |
5,16 |
|
11 |
3 |
0,90 |
1,42 |
2,01 |
6,41 |
9,11 |
14,47 |
|
|
4 |
1,35 |
1,61 |
2,06 |
5,46 |
7,04 |
9,98 |
|
|
5 |
1,43 |
1,64 |
2,05 |
4,90 |
6,07 |
7,83 |
|
|
6 |
1,45 |
1,64 |
2,04 |
4,58 |
5,52 |
6,96 |
|
|
7 |
1,45 |
1,64 |
2,03 |
4,36 |
4,16 |
6,34 |
|
|
8 |
1,45 |
1,64 |
2,01 |
4,15 |
4,87 |
5,82 |
|
|
9 |
1,44 |
1,64 |
2,00 |
4,01 |
4,63 |
5,54 |
|
|
10 |
1,44 |
1,64 |
1,99 |
3,87 |
4,44 |
5,23 |
|
|
11 |
1,45 |
1,64 |
1,98 |
3,76 |
4,26 |
4,94 |
|
12 |
3 |
0,75 |
1,37 |
1,98 |
6,00 |
8,40 |
12,96 |
|
|
4 |
1,34 |
1,60 |
2,05 |
5,17 |
6,60 |
9,07 |
|
|
5 |
1,44 |
1,66 |
2,05 |
4,72 |
5,79 |
7,35 |
|
|
6 |
1,46 |
1,67 |
2,04 |
4,41 |
5,31 |
6,61 |
|
|
7 |
1,47 |
1,67 |
2,03 |
4,21 |
4,98 |
6,09 |
|
|
8 |
1,47 |
1,66 |
2,02 |
4,06 |
4,75 |
5,71 |
|
|
9 |
1,46 |
1,66 |
2,01 |
3,94 |
4,53 |
5,40 |
|
|
10 |
1,47 |
1,65 |
2,00 |
3,87 |
4,37 |
5,11 |
|
|
11 |
1,46 |
1,64 |
1,99 |
3,72 |
4,23 |
4,88 |
|
|
12 |
1,47 |
1,64 |
1,99 |
3,62 |
4,07 |
4,68 |
|
13 |
3 |
0,72 |
1,34 |
1,99 |
5,88 |
8,16 |
12,45 |
|
|
4 |
1,31 |
1,60 |
2,06 |
5,10 |
6,45 |
8,82 |
|
|
5 |
1,45 |
1,67 |
2,07 |
4,71 |
5,75 |
7,32 |
|
|
6 |
1,48 |
1,68 |
2,07 |
4,43 |
5,30 |
6,49 |
|
|
7 |
1,49 |
1,68 |
2,06 |
4,23 |
4,96 |
6,02 |
|
|
8 |
1,49 |
1,68 |
2,04 |
4,06 |
4,73 |
5,63 |
|
|
9 |
1,49 |
1,68 |
2,03 |
3,94 |
4,55 |
5,32 |
|
|
10 |
1,49 |
1,68 |
2,03 |
3,83 |
4,37 |
5,11 |
|
|
11 |
1,49 |
1,68 |
2,02 |
3,74 |
4,23 |
4,90 |
|
|
12 |
1,49 |
1,67 |
2,01 |
3,65 |
4,09 |
4,73 |
|
|
13 |
1,49 |
1,67 |
2,01 |
3,57 |
3,97 |
4,51 |
|
14 |
3 |
0,57 |
1,25 |
1,93 |
5,56 |
7,69 |
11,56 |
|
|
4 |
1,29 |
1,59 |
2,03 |
4,93 |
6,17 |
8,28 |
|
|
5 |
1,46 |
1,67 |
2,05 |
4,58 |
5,54 |
6,96 |
|
|
6 |
1,51 |
1,69 |
2,05 |
4,33 |
5,12 |
6,27 |
|
|
7 |
1,52 |
1,69 |
2,04 |
4,15 |
4,82 |
5,75 |
|
|
8 |
1,52 |
1,69 |
2,03 |
4,03 |
4,61 |
5,47 |
|
|
9 |
1,52 |
1,69 |
2,03 |
3,90 |
4,45 |
5,18 |
|
|
10 |
1,51 |
1,68 |
2,02 |
3,78 |
4,30 |
4,94 |
|
|
11 |
1,51 |
1,68 |
2,01 |
3,71 |
4,20 |
4,79 |
|
|
12 |
1,51 |
1,68 |
2,01 |
3,64 |
4,09 |
4,67 |
|
|
13 |
1,51 |
1,68 |
2,00 |
3,55 |
3,98 |
4,51 |
|
|
14 |
1,51 |
1,68 |
2,00 |
3,46 |
3,85 |
4,36 |
|
15 |
3 |
0,43 |
1,19 |
1,91 |
5,39 |
7,23 |
10,78 |
|
|
4 |
1,26 |
1,59 |
2,03 |
4,78 |
5,95 |
7,94 |
|
|
5 |
1,44 |
1,67 |
2,06 |
4,43 |
5,36 |
6,85 |
|
|
6 |
1,50 |
1,69 |
2,06 |
4,22 |
4,97 |
6,19 |
|
|
7 |
1,52 |
1,70 |
2,06 |
4,08 |
4,72 |
5,77 |
|
|
8 |
1,52 |
1,70 |
2,05 |
3,95 |
4,57 |
5,40 |
|
|
9 |
1,52 |
1,69 |
2,04 |
3,85 |
4,40 |
5,16 |
|
|
10 |
1,52 |
1,69 |
2,04 |
3,76 |
4,26 |
4,95 |
|
|
11 |
1,52 |
1,69 |
2,03 |
3,69 |
4,15 |
4,76 |
|
|
12 |
1,52 |
1,69 |
2,02 |
3,62 |
4,08 |
4,62 |
|
|
13 |
1,52 |
1,68 |
2,01 |
3,55 |
3,98 |
4,51 |
|
|
14 |
1,51 |
1,69 |
2,01 |
3,49 |
3,89 |
4,39 |
|
|
15 |
1,52 |
1,68 |
2,01 |
3,41 |
3,77 |
4,23 |
при вероятности
Таблица 70
|
|
|
| |||||
|
|
|
0,05 |
0,10 |
0,25 |
0,90 |
0,95 |
0,98 |
|
3 |
3 |
1,64 |
2,04 |
2,94 |
11,85 |
17,21 |
27,32 |
|
4 |
3 |
1,73 |
2,11 |
2,98 |
12,17 |
17,55 |
27,59 |
|
|
4 |
1,69 |
2,04 |
2,78 |
8,40 |
10,88 |
15,06 |
|
5 |
3 |
1,79 |
2,16 |
3,00 |
12,07 |
17,36 |
28,30 |
|
|
4 |
1,76 |
2,10 |
2,82 |
8,56 |
11,14 |
15,51 |
|
|
5 |
1,74 |
2,06 |
2,72 |
7,06 |
8,68 |
11,14 |
|
6 |
3 |
1,83 |
2,20 |
2,99 |
11,53 |
16,66 |
26,85 |
|
|
4 |
1,83 |
2,15 |
2,84 |
8,47 |
10,95 |
15,32 |
|
|
5 |
1,81 |
2,12 |
2,76 |
7,08 |
8,82 |
11,58 |
|
|
6 |
1,80 |
2,10 |
2,70 |
6,27 |
7,53 |
9,39 |
|
7 |
3 |
1,87 |
2,22 |
2,97 |
11,20 |
16,07 |
25,31 |
|
|
4 |
1,88 |
2,19 |
2,86 |
8,39 |
10,80 |
14,80 |
|
|
5 |
1,86 |
2,16 |
2,78 |
7,12 |
8,84 |
11,18 |
|
|
6 |
1,84 |
2,14 |
2,72 |
6,33 |
7,61 |
9,40 |
|
|
7 |
1,85 |
2,14 |
2,68 |
5,76 |
6,73 |
8,19 |
|
8 |
3 |
1,90 |
2,24 |
2,96 |
11,02 |
15,76 |
24,57 |
|
|
4 |
1,91 |
2,22 |
2,87 |
8,19 |
10,74 |
15,22 |
|
|
5 |
1,90 |
2,20 |
2,79 |
7,70 |
8,78 |
11,57 |
|
|
6 |
1,89 |
2,18 |
2,75 |
6,35 |
7,67 |
9,43 |
|
|
7 |
1,89 |
2,17 |
2,71 |
5,83 |
6,91 |
8,38 |
|
|
8 |
1,89 |
2,17 |
2,69 |
5,44 |
6,29 |
7,50 |
|
9 |
3 |
1,93 |
2,26 |
2,95 |
10,71 |
15,33 |
23,80 |
|
|
4 |
1,96 |
2,25 |
2,88 |
8,02 |
10,40 |
14,41 |
|
|
5 |
1,95 |
2,23 |
2,80 |
6,90 |
8,59 |
11,05 |
|
|
6 |
1,95 |
2,22 |
2,76 |
6,27 |
7,51 |
9,46 |
|
|
7 |
1,94 |
2,21 |
2,73 |
5,86 |
6,91 |
8,40 |
|
|
8 |
1,94 |
2,20 |
2,70 |
5,53 |
6,39 |
7,73 |
|
|
9 |
1,95 |
2,19 |
2,68 |
5,72 |
6,00 |
7,09 |
|
10 |
3 |
1,91 |
2,26 |
2,91 |
10,24 |
14,50 |
23,00 |
|
|
4 |
1,98 |
2,27 |
2,86 |
7,81 |
10,12 |
13,69 |
|
|
5 |
1,97 |
2,24 |
2,80 |
6,87 |
8,39 |
11,00 |
|
|
6 |
1,97 |
2,23 |
2,76 |
6,24 |
7,50 |
9,42 |
|
|
7 |
1,96 |
2,22 |
2,73 |
5,79 |
6,83 |
8,29 |
|
|
8 |
1,96 |
2,21 |
3,71 |
5,52 |
6,40 |
7,61 |
|
|
9 |
1,96 |
2,21 |
2,69 |
5,23 |
6,01 |
7,12 |
|
|
10 |
1,96 |
2,21 |
2,69 |
4,98 |
5,67 |
6,65 |
|
11 |
3 |
1,93 |
2,25 |
2,88 |
9,87 |
14,11 |
22,60 |
|
|
4 |
2,01 |
2,27 |
2,83 |
7,71 |
10,03 |
14,44 |
|
|
5 |
2,01 |
2,26 |
2,78 |
6,72 |
8,34 |
10,93 |
|
|
6 |
2,00 |
2,24 |
2,74 |
6,16 |
7,42 |
9,39 |
|
|
7 |
1,99 |
2,23 |
2,72 |
5,79 |
6,83 |
8,42 |
|
|
8 |
1,99 |
2,22 |
2,70 |
5,46 |
6,38 |
7,65 |
|
|
9 |
1,98 |
2,22 |
2,68 |
5,23 |
6,04 |
7,23 |
|
|
10 |
2,00 |
2,22 |
2,67 |
5,03 |
5,75 |
6,73 |
|
|
11 |
2,00 |
2,22 |
2,66 |
4,85 |
5,49 |
6,35 |
|
12 |
3 |
1,91 |
2,26 |
2,87 |
9,41 |
13,40 |
21,39 |
|
|
4 |
2,02 |
2,28 |
2,84 |
7,42 |
9,56 |
13,27 |
|
|
5 |
2,03 |
2,28 |
2,78 |
6,54 |
8,08 |
10,40 |
|
|
6 |
2,02 |
2,27 |
2,75 |
5,97 |
7,22 |
9,00 |
|
|
7 |
2,02 |
2,26 |
2,73 |
5,63 |
6,66 |
8,08 |
|
|
8 |
2,01 |
2,25 |
2,71 |
5,36 |
6,27 |
7,49 |
|
|
9 |
2,00 |
2,24 |
2,69 |
5,16 |
5,95 |
7,06 |
|
|
10 |
2,01 |
2,23 |
2,67 |
4,99 |
5,67 |
6,63 |
|
|
11 |
2,01 |
2,24 |
2,67 |
4,84 |
5,47 |
6,29 |
|
|
12 |
2,02 |
2,24 |
2,66 |
4,68 |
5,26 |
6,00 |
|
13 |
3 |
1,92 |
2,27 |
2,88 |
9,23 |
13,11 |
20,76 |
|
|
4 |
2,05 |
2,31 |
2,84 |
7,38 |
9,47 |
13,09 |
|
|
5 |
2,06 |
2,30 |
2,81 |
6,57 |
8,04 |
10,25 |
|
|
6 |
2,05 |
2,29 |
2,78 |
6,03 |
7,24 |
8,89 |
|
|
7 |
2,05 |
2,28 |
2,75 |
5,65 |
6,68 |
8,10 |
|
|
8 |
2,04 |
2,27 |
1,74 |
5,40 |
6,29 |
7,43 |
|
|
9 |
2,04 |
2,27 |
2,72 |
5,17 |
6,00 |
6,99 |
|
|
10 |
2,04 |
2,27 |
2,70 |
5,01 |
5,70 |
6,66 |
|
|
11 |
2,04 |
2,27 |
2,70 |
4,87 |
5,50 |
6,36 |
|
|
12 |
2,04 |
2,27 |
2,69 |
4,73 |
5,30 |
6,12 |
|
|
13 |
2,05 |
2,27 |
2,68 |
4,61 |
5,12 |
5,80 |
|
14 |
3 |
1,92 |
2,26 |
2,84 |
8,84 |
12,73 |
19,14 |
|
|
4 |
2,06 |
2,31 |
2,82 |
7,18 |
9,10 |
12,45 |
|
|
5 |
2,08 |
2,31 |
2,79 |
6,38 |
7,82 |
9,93 |
|
|
6 |
2,08 |
2,30 |
2,76 |
5,91 |
7,07 |
8,71 |
|
|
7 |
2,07 |
2,29 |
2,73 |
5,58 |
6,53 |
7,78 |
|
|
8 |
2,07 |
2,28 |
2,72 |
5,35 |
6,16 |
7,30 |
|
|
9 |
2,07 |
2,28 |
2,71 |
5,14 |
5,88 |
6,92 |
|
|
10 |
2,06 |
2,27 |
2,70 |
4,98 |
5,65 |
6,49 |
|
|
11 |
2,07 |
2,28 |
2,69 |
4,86 |
5,48 |
6,26 |
|
|
12 |
2,07 |
2,28 |
2,68 |
4,73 |
5,31 |
6,06 |
|
|
13 |
2,07 |
2,29 |
2,68 |
4,61 |
5,14 |
5,80 |
|
|
14 |
2,08 |
2,28 |
2,66 |
4,48 |
4,97 |
5,60 |
|
15 |
3 |
1,88 |
2,24 |
2,84 |
8,75 |
12,22 |
18,38 |
|
|
4 |
2,06 |
2,31 |
2,83 |
7,00 |
8,90 |
11,93 |
|
|
5 |
2,09 |
2,32 |
2,80 |
6,25 |
7,64 |
9,79 |
|
|
6 |
2,09 |
2,31 |
2,79 |
5,79 |
6,91 |
8,55 |
|
|
7 |
2,08 |
2,30 |
2,76 |
5,50 |
6,41 |
7,90 |
|
|
8 |
2,08 |
2,29 |
2,74 |
5,29 |
6,10 |
7,26 |
|
|
9 |
2,07 |
2,29 |
2,73 |
5,11 |
5,81 |
6,87 |
|
|
10 |
2,07 |
2,28 |
2,72 |
4,96 |
5,61 |
6,50 |
|
|
11 |
2,07 |
2,28 |
2,70 |
4,84 |
5,43 |
6,22 |
|
|
12 |
2,07 |
2,28 |
2,70 |
4,73 |
5,31 |
6,00 |
|
|
13 |
2,07 |
2,28 |
2,69 |
4,63 |
5,17 |
5,88 |
|
|
14 |
2,07 |
2,28 |
2,68 |
4,53 |
5,02 |
5,66 |
|
|
15 |
2,08 |
2,28 |
2,68 |
4,43 |
4,88 |
5,46 |
при вероятности
Таблица 71
|
|
|
| |||||
|
|
|
0,05 |
0,10 |
0,25 |
0,90 |
0,95 |
0,98 |
|
3 |
3 |
2,75 |
3,32 |
4,63 |
18,15 |
26,71 |
42,07 |
|
4 |
3 |
2,87 |
3,44 |
4,74 |
19,38 |
27,97 |
43,72 |
|
|
4 |
2,82 |
3,31 |
4,38 |
12,79 |
16,62 |
23,12 |
|
5 |
3 |
2,95 |
3,47 |
4,80 |
19,73 |
28,71 |
46,68 |
|
|
4 |
2,86 |
3,37 |
4,44 |
13,31 |
17,41 |
24,31 |
|
|
5 |
2,87 |
3,32 |
4,28 |
10,75 |
13,23 |
16,87 |
|
6 |
3 |
3,02 |
3,55 |
4,80 |
19,28 |
28,02 |
45,73 |
|
|
4 |
2,96 |
3,45 |
4,49 |
13,49 |
17,54 |
24,27 |
|
|
5 |
2,94 |
3,38 |
4,33 |
10,96 |
13,67 |
17,96 |
|
|
6 |
2,94 |
3,39 |
4,25 |
9,49 |
11,41 |
14,37 |
|
7 |
3 |
3,11 |
3,61 |
4,81 |
19,27 |
27,76 |
44,93 |
|
|
4 |
3,04 |
3,49 |
4,52 |
13,53 |
17,47 |
23,96 |
|
|
5 |
3,00 |
3,44 |
4,37 |
11,20 |
13,91 |
17,78 |
|
|
6 |
3,01 |
3,41 |
4,26 |
9,75 |
11,74 |
14,36 |
|
|
7 |
3,02 |
3,43 |
4,21 |
8,75 |
10,20 |
12,38 |
|
8 |
3 |
3,12 |
3,65 |
4,82 |
19,24 |
27,78 |
44,29 |
|
|
4 |
3,07 |
3,53 |
4,54 |
13,42 |
17,64 |
25,03 |
|
|
5 |
3,05 |
3,47 |
4,39 |
11,12 |
13,92 |
18,42 |
|
|
6 |
3,04 |
3,45 |
4,30 |
9,82 |
11,87 |
14,78 |
|
|
7 |
3,06 |
3,47 |
4,24 |
8,92 |
10,52 |
12,89 |
|
|
8 |
3,08 |
3,47 |
4,20 |
8,27 |
9,52 |
11,35 |
|
9 |
3 |
3,20 |
3,66 |
4,81 |
19,00 |
27,91 |
43,02 |
|
|
4 |
3,12 |
3,56 |
4,56 |
13,28 |
17,57 |
24,34 |
|
|
5 |
3,10 |
3,52 |
4,40 |
10,98 |
13,78 |
17,99 |
|
|
6 |
3,10 |
3,52 |
4,32 |
9,82 |
11,78 |
14,84 |
|
|
7 |
3,10 |
3,61 |
4,27 |
9,06 |
10,66 |
12,96 |
|
|
8 |
3,12 |
3,50 |
4,24 |
8,44 |
9,75 |
11,85 |
|
|
9 |
3,17 |
3,50 |
4,20 |
7,90 |
9,04 |
10,71 |
|
10 |
3 |
3,20 |
3,68 |
4,77 |
18,61 |
27,05 |
43,21 |
|
|
4 |
3,16 |
3,60 |
4,53 |
13,12 |
17,17 |
23,48 |
|
|
5 |
3,13 |
3,54 |
4,41 |
11,05 |
13,70 |
17,82 |
|
|
6 |
3,11 |
3,51 |
4,33 |
9,81 |
11,86 |
15,01 |
|
|
7 |
3,12 |
3,50 |
4,28 |
8,99 |
10,66 |
13,03 |
|
|
8 |
3,15 |
3,50 |
4,23 |
8,49 |
9,88 |
11,69 |
|
|
9 |
3,16 |
3,51 |
4,21 |
7,97 |
9,17 |
10,82 |
|
|
10 |
3,19 |
3,53 |
4,18 |
7,57 |
8,57 |
10,03 |
|
11 |
3 |
3,22 |
3,67 |
4,75 |
18,19 |
26,45 |
43,82 |
|
|
4 |
3,16 |
3,58 |
4,53 |
13,02 |
17,25 |
24,97 |
|
|
5 |
3,15 |
3,55 |
4,39 |
10,99 |
13,66 |
18,13 |
|
|
6 |
3,14 |
3,52 |
4,30 |
9,79 |
11,86 |
15,02 |
|
|
7 |
3,16 |
3,51 |
4,26 |
9,03 |
10,72 |
13,30 |
|
|
8 |
3,16 |
3,51 |
4,23 |
8,43 |
9,86 |
11,88 |
|
|
9 |
3,17 |
3,51 |
4,20 |
8,02 |
9,24 |
11,08 |
|
|
10 |
3,20 |
3,53 |
4,18 |
7,67 |
8,73 |
10,20 |
|
|
11 |
3,24 |
3,55 |
4,17 |
7,36 |
8,31 |
9,57 |
|
12 |
3 |
3,28 |
3,72 |
4,77 |
17,59 |
25,73 |
41,44 |
|
|
4 |
3,22 |
3,62 |
4,52 |
12,72 |
16,60 |
23,41 |
|
|
5 |
3,19 |
3,58 |
4,59 |
10,68 |
13,37 |
17,35 |
|
|
6 |
3,19 |
3,55 |
4,31 |
9,61 |
11,60 |
14,59 |
|
|
7 |
3,28 |
3,54 |
4,27 |
8,85 |
10,55 |
12,65 |
|
|
8 |
3,18 |
3,54 |
4,24 |
8,34 |
9,75 |
11,64 |
|
|
9 |
3,18 |
3,53 |
4,21 |
7,98 |
9,18 |
10,90 |
|
|
10 |
3,20 |
3,54 |
4,18 |
7,66 |
8,68 |
10,17 |
|
|
11 |
3,23 |
3,55 |
4,17 |
7,37 |
8,31 |
9,53 |
|
|
12 |
3,27 |
3,57 |
4,17 |
7,09 |
7,96 |
9,03 |
|
13 |
3 |
3,30 |
3,74 |
4,78 |
17,58 |
25,37 |
40,28 |
|
|
4 |
3,25 |
3,66 |
4,58 |
12,81 |
16,56 |
23,73 |
|
|
5 |
3,22 |
3,60 |
4,43 |
10,86 |
13,47 |
17,15 |
|
|
6 |
3,21 |
3,57 |
4,35 |
9,71 |
11,72 |
14,47 |
|
|
7 |
3,21 |
3,57 |
4,30 |
8,97 |
10,61 |
13,04 |
|
|
8 |
3,22 |
3,57 |
4,28 |
8,46 |
9,88 |
11,74 |
|
|
9 |
3,23 |
3,56 |
4,25 |
8,02 |
9,27 |
10,88 |
|
|
10 |
3,24 |
3,57 |
4,23 |
7,72 |
8,80 |
10,25 |
|
|
11 |
3,25 |
3,58 |
4,22 |
7,46 |
8,42 |
9,65 |
|
|
12 |
3,27 |
3,60 |
4,21 |
7,21 |
8,03 |
9,27 |
|
|
13 |
3,30 |
3,61 |
4,20 |
6,99 |
7,75 |
8,76 |
|
14 |
3 |
3,30 |
3,75 |
4,75 |
17,23 |
25,09 |
39,16 |
|
|
4 |
3,28 |
3,68 |
4,52 |
12,48 |
16,19 |
22,41 |
|
|
5 |
3,25 |
3,62 |
4,40 |
10,64 |
13,22 |
16,89 |
|
|
6 |
3,24 |
3,58 |
4,33 |
9,59 |
11,55 |
14,29 |
|
|
7 |
3,23 |
3,58 |
4,28 |
8,88 |
10,47 |
12,51 |
|
|
8 |
3,24 |
3,58 |
4,25 |
8,40 |
9,71 |
11,54 |
|
|
9 |
3,25 |
3,58 |
4,23 |
8,00 |
9,17 |
10,81 |
|
|
10 |
3,26 |
3,58 |
4,22 |
7,71 |
8,72 |
10,06 |
|
|
11 |
3,28 |
3,60 |
4,20 |
7,46 |
8,42 |
9,61 |
|
|
12 |
3,31 |
3,61 |
4,20 |
7,25 |
8,11 |
9,25 |
|
|
13 |
3,31 |
3,62 |
4,19 |
7,03 |
7,82 |
8,81 |
|
|
14 |
3,34 |
3,63 |
4,17 |
9,81 |
7,49 |
8,45 |
|
15 |
3 |
3,34 |
3,77 |
4,78 |
17,15 |
24,54 |
38,14 |
|
|
4 |
3,29 |
3,69 |
4,55 |
12,41 |
15,96 |
21,82 |
|
|
5 |
3,28 |
3,64 |
4,42 |
10,56 |
12,94 |
16,99 |
|
|
6 |
3,26 |
3,61 |
4,37 |
9,45 |
11,38 |
14,24 |
|
|
7 |
3,25 |
3,59 |
4,31 |
8,81 |
10,31 |
12,84 |
|
|
8 |
3,25 |
3,59 |
4,27 |
8,36 |
9,36 |
11,58 |
|
|
9 |
3,26 |
3,58 |
4,26 |
8,00 |
9,11 |
10,79 |
|
|
10 |
3,27 |
3,59 |
4,24 |
7,71 |
8,72 |
10,06 |
|
|
11 |
3,26 |
3,59 |
4,21 |
7,48 |
8,37 |
9,61 |
|
|
12 |
3,29 |
3,61 |
4,21 |
7,29 |
8,17 |
9,24 |
|
|
13 |
3,30 |
3,61 |
4,20 |
7,09 |
7,89 |
8,92 |
|
|
14 |
3,32 |
3,62 |
4,19 |
6,92 |
7,63 |
8,59 |
|
|
15 |
3,35 |
3,62 |
4,19 |
6,70 |
7,37 |
8,24 |
при вероятности
Таблица 72
|
|
Квантили | |||||||||
|
|
0,75 |
0,90 |
0,95 |
0,975 |
0,990 |
0,995 |
0,9975 |
0,999 |
0,9995 |
|
|
1 |
1,0000 |
3,0777 |
6,3138 |
12,7062 |
31,8205 |
63,6567 |
127,3213 |
318,3088 |
636,6192 |
1 |
|
2 |
0,8165 |
1,8856 |
2,9200 |
4,3027 |
6,9646 |
9,9248 |
14,0890 |
22,3271 |
31,5991 |
2 |
|
3 |
7649 |
6377 |
3534 |
3,1824 |
4,5407 |
5,8409 |
7,4533 |
10,2145 |
12,9240 |
3 |
|
4 |
7407 |
5332 |
1318 |
2,7764 |
3,7469 |
4,6041 |
5,5976 |
7,1732 |
8,6103 |
4 |
|
5 |
7267 |
4759 |
0150 |
5706 |
3649 |
0321 |
4,7733 |
5,8934 |
6,8688 |
5 |
|
6 |
0,7176 |
1,4398 |
1,9432 |
2,4469 |
3,1427 |
3,7074 |
4,3168 |
5,2076 |
5,9588 |
6 |
|
7 |
7111 |
4149 |
8946 |
3646 |
2,9980 |
4995 |
0293 |
4,7853 |
4079 |
7 |
|
8 |
7064 |
3968 |
8595 |
3060 |
8965 |
3554 |
3,8325 |
5008 |
0413 |
8 |
|
9 |
7027 |
3830 |
8331 |
2622 |
8214 |
2498 |
6897 |
2968 |
4,7809 |
9 |
|
10 |
6998 |
3722 |
8125 |
2281 |
7638 |
1693 |
5814 |
1437 |
5869 |
10 |
|
11 |
0,6974 |
1,3634 |
1,7959 |
2,2010 |
2,7181 |
3,1058 |
3,4966 |
4,0247 |
4,4370 |
11 |
|
12 |
6955 |
3562 |
7823 |
1788 |
6810 |
0545 |
4284 |
3,9296 |
3178 |
12 |
|
13 |
6938 |
3502 |
7709 |
1604 |
6503 |
0123 |
3725 |
8520 |
2208 |
13 |
|
14 |
6924 |
3450 |
7613 |
1448 |
6245 |
2,9768 |
3257 |
7874 |
1405 |
14 |
|
15 |
6912 |
3406 |
7530 |
1314 |
6025 |
9467 |
2860 |
7328 |
0728 |
15 |
|
16 |
0,6901 |
1,3368 |
1,7459 |
2,1199 |
2,5835 |
2,9208 |
3,2520 |
3,6862 |
4,0150 |
16 |
|
17 |
6892 |
3334 |
7396 |
1098 |
5669 |
8982 |
2224 |
6458 |
3,9651 |
17 |
|
18 |
6884 |
3304 |
7341 |
1009 |
5524 |
8784 |
1966 |
6105 |
9216 |
18 |
|
19 |
6876 |
3277 |
7291 |
0930 |
5395 |
8609 |
1737 |
5794 |
8834 |
19 |
|
20 |
6870 |
3253 |
7247 |
0860 |
5280 |
8453 |
1534 |
5518 |
8495 |
20 |
|
21 |
0,6864 |
1,3232 |
1,7207 |
2,0796 |
2,5176 |
2,8314 |
3,1352 |
3,5272 |
3,8193 |
21 |
|
22 |
6858 |
3212 |
7171 |
0739 |
5083 |
8188 |
1188 |
5050 |
7921 |
22 |
|
23 |
0,6853 |
1,3195 |
1,7139 |
2,0687 |
2,4999 |
2,8073 |
3,1040 |
3,4850 |
3,7676 |
23 |
|
24 |
6848 |
3178 |
7109 |
0639 |
4922 |
7969 |
0905 |
4668 |
7455 |
24 |
|
25 |
6844 |
3163 |
7081 |
0595 |
4851 |
7874 |
0782 |
4502 |
7251 |
25 |
|
26 |
0,6840 |
1,3150 |
1,7056 |
2,0555 |
2,4786 |
2,7787 |
3,0669 |
3,4350 |
3,7066 |
26 |
|
27 |
6837 |
3137 |
7033 |
0518 |
4727 |
7707 |
0565 |
4210 |
6896 |
27 |
|
28 |
6834 |
3125 |
7011 |
0484 |
4671 |
7633 |
0469 |
4082 |
6739 |
28 |
|
29 |
6830 |
3114 |
6991 |
0452 |
4620 |
7564 |
0380 |
3962 |
6594 |
29 |
|
30 |
6828 |
3104 |
6973 |
0423 |
4573 |
7500 |
0298 |
3852 |
6460 |
30 |
|
32 |
0,6822 |
1,3086 |
1,6939 |
2,0369 |
2,4487 |
2,7385 |
3,0149 |
3,3653 |
3,6218 |
32 |
|
34 |
6818 |
3070 |
6909 |
0322 |
4411 |
7284 |
0020 |
3479 |
6007 |
34 |
|
36 |
6814 |
3055 |
6883 |
0281 |
4345 |
7195 |
2,9905 |
3326 |
5821 |
36 |
|
38 |
6810 |
3042 |
6860 |
0244 |
4286 |
7116 |
9803 |
3190 |
5657 |
38 |
|
40 |
6807 |
3031 |
6839 |
0211 |
4233 |
7045 |
9712 |
3069 |
5510 |
40 |
|
42 |
0,6804 |
1,3020 |
1,6820 |
2,0181 |
2,4185 |
2,6981 |
2,9630 |
3,2960 |
3,5377 |
42 |
|
44 |
6801 |
3011 |
6802 |
0154 |
4141 |
6923 |
9555 |
2861 |
5258 |
44 |
|
46 |
6799 |
3002 |
6787 |
0129 |
4102 |
6870 |
9488 |
2771 |
5150 |
46 |
|
48 |
6796 |
2994 |
6772 |
0106 |
4066 |
6822 |
9426 |
2689 |
5051 |
48 |
|
50 |
6794 |
2987 |
6759 |
0086 |
4033 |
6778 |
9370 |
2614 |
4960 |
50 |
|
55 |
0,6790 |
1,2971 |
1,6730 |
2,0040 |
2,3961 |
2,6682 |
2,9247 |
3,2561 |
3,4764 |
55 |
|
60 |
6786 |
2958 |
6706 |
0003 |
3901 |
6603 |
9146 |
2317 |
4602 |
60 |
|
65 |
6783 |
2947 |
6686 |
1,9971 |
3851 |
6536 |
9060 |
2204 |
4466 |
65 |
|
70 |
6780 |
2938 |
6669 |
9944 |
3808 |
6479 |
8987 |
2108 |
4350 |
70 |
|
80 |
6776 |
2922 |
6641 |
9901 |
3739 |
6387 |
8870 |
1953 |
4163 |
80 |
|
90 |
0,6772 |
1,2910 |
1,6620 |
1,9867 |
2,3685 |
2,6316 |
2,8779 |
3,1833 |
3,4019 |
90 |
|
100 |
6770 |
2901 |
6602 |
9840 |
3642 |
6259 |
8707 |
1737 |
3905 |
100 |
|
120 |
6765 |
2886 |
6577 |
9799 |
3578 |
6174 |
8599 |
1595 |
1735 |
120 |
|
150 |
0,6761 |
1,2872 |
1,6551 |
1,9759 |
2,3515 |
2,6090 |
2,8492 |
3,1455 |
3,3566 |
150 |
|
200 |
6757 |
2858 |
6525 |
9719 |
3451 |
6006 |
8385 |
1315 |
3398 |
200 |
|
250 |
0,6755 |
1,2849 |
1,6510 |
1,9695 |
2,3414 |
2,5956 |
2,8322 |
3,1232 |
3,3299 |
250 |
|
300 |
6753 |
2844 |
6499 |
9679 |
3388 |
5923 |
8279 |
1176 |
3233 |
300 |
|
400 |
6751 |
2837 |
6487 |
9659 |
3357 |
5882 |
8227 |
1107 |
3150 |
400 |
|
500 |
6750 |
2832 |
6479 |
9647 |
3338 |
5857 |
8195 |
1066 |
3101 |
500 |
|
|
6745 |
2816 |
6449 |
9600 |
3263 |
5758 |
8070 |
0902 |
2905 |
|
Таблица 73
Значения 
|
|
|
|
|
| |||||||||||||||
|
|
Доверительная вероятность | ||||||||||||||||||
|
|
0,975* |
0,90 |
0,95 |
0,99 |
0,975* |
0,90 |
0,95 |
0,99 |
0,975* |
0,90 |
0,95 |
0,99 |
0,975* |
0,90 |
0,95 |
0,99 | |||
|
3 |
1,464 |
2,501 |
3,152 |
4,396 |
2,602 |
4,258 |
5,310 |
7,340 |
3,804 |
6,158 |
7,655 |
10,552 |
|
|
|
| |||
|
4 |
1,256 |
2,134 |
2,680 |
3,726 |
1,972 |
3,187 |
3,957 |
5,437 |
2,619 |
4,163 |
5,145 |
7,042 |
|
|
|
| |||
|
5 |
1,152 |
1,961 |
2,463 |
3,421 |
1,698 |
2,742 |
3,400 |
4,666 |
2,149 |
3,407 |
4,202 |
5,741 |
|
|
|
| |||
|
6 |
1,087 |
1,860 |
2,336 |
3,243 |
1,540 |
2,494 |
3,091 |
4,242 |
1,895 |
3,006 |
3,707 |
5,062 |
2,849 |
4,408 |
5,409 |
7,334 | |||
|
7 |
1,043 |
1,791 |
2,250 |
3,126 |
1,435 |
2,333 |
2,894 |
3,972 |
1,732 |
2,755 |
3,399 |
4,641 |
2,490 |
3,856 |
4,730 |
6,411 | |||
|
8 |
1,010 |
1,740 |
2,192 |
3,042 |
1,360 |
2,219 |
2,755 |
3,783 |
1,617 |
2,582 |
3,188 |
4,353 |
2,252 |
3,496 |
4,287 |
5,811 | |||
|
9 |
0,984 |
1,702 |
2,141 |
2,977 |
1,302 |
2,133 |
2,649 |
3,641 |
1,532 |
2,454 |
3,031 |
4,143 |
2,085 |
3,242 |
3,971 |
5,389 | |||
|
10 |
0,964 |
1,671 |
2,103 |
2,927 |
1,257 |
2,065 |
2,568 |
3,532 |
1,465 |
2,355 |
2,911 |
3,981 |
1,954 |
3,048 |
3,739 |
5,075 | |||
|
11 |
0,947 |
1,646 |
2,073 |
2,885 |
1,219 |
2,012 |
2,503 |
3,444 |
1,411 |
2,275 |
2,815 |
3,852 |
1,854 |
2,897 |
3,557 |
4,828 | |||
|
12 |
0,933 |
1,624 |
2,048 |
2,851 |
1,188 |
1,966 |
2,448 |
3,371 |
1,366 |
2,210 |
2,736 |
3,747 |
1,771 |
2,773 |
3,410 |
4,633 | |||
|
13 |
0,919 |
1,606 |
2,026 |
2,822 |
1,162 |
1,928 |
2,403 |
3,310 |
1,329 |
2,155 |
2,670 |
3,659 |
1,702 |
2,677 |
3,290 |
4,472 | |||
|
14 |
0,909 |
1,591 |
2,007 |
2,796 |
1,139 |
1,895 |
2,363 |
3,257 |
1,296 |
2,108 |
2,614 |
3,585 |
1,645 |
2,592 |
3,189 |
4,336 | |||
|
15 |
0,899 |
1,577 |
1,991 |
2,776 |
1,119 |
1,866 |
2,329 |
3,212 |
1,268 |
2,068 |
2,566 |
3,520 |
1,596 |
2,521 |
3,102 |
4,224 | |||
|
16 |
0,891 |
1,566 |
1,977 |
2,756 |
1,101 |
1,842 |
2,299 |
3,172 |
1,242 |
2,032 |
2,523 |
3,463 |
1,553 |
2,458 |
3,028 |
4,124 | |||
|
17 |
0,883 |
1,554 |
1,964 |
2,739 |
1,085 |
1,820 |
2,272 |
3,136 |
1,220 |
2,001 |
2,486 |
3,415 |
1,514 |
2,405 |
2,962 |
4,038 | |||
|
18 |
0,876 |
1,544 |
1,951 |
2,723 |
1,071 |
1,800 |
2,249 |
3,106 |
1,200 |
1,974 |
2,453 |
3,370 |
1,481 |
2,357 |
2,906 |
3,961 | |||
|
19 |
0,870 |
1,536 |
1,942 |
2,710 |
1,058 |
1,781 |
2,228 |
3,078 |
1,183 |
1,949 |
2,423 |
3,331 |
1,450 |
2,315 |
2,855 |
3,893 | |||
|
20 |
0,865 |
1,528 |
1,933 |
2,697 |
1,046 |
1,765 |
2,208 |
3,052 |
1,167 |
1,926 |
3,396 |
3,295 |
1,424 |
2,275 |
2,807 |
3,832 | |||
|
21 |
0,859 |
1,520 |
1,923 |
2,686 |
1,035 |
1,750 |
2,190 |
3,028 |
1,152 |
1,905 |
2,371 |
3,262 |
1,397 |
2,241 |
2,768 |
3,776 | |||
|
22 |
0,854 |
1,514 |
1,916 |
2,675 |
1,025 |
1,736 |
2,174 |
3,007 |
1,138 |
1,887 |
2,350 |
3,233 |
1,376 |
2,208 |
2,729 |
3,727 | |||
|
23 |
0,849 |
1,508 |
1,907 |
2,665 |
1,016 |
1,724 |
2,159 |
2,987 |
1,126 |
1,869 |
2,329 |
3,206 |
1,355 |
2,179 |
2,693 |
3,680 | |||
|
24 |
0,845 |
1,502 |
1,901 |
2,656 |
1,007 |
1,712 |
2,145 |
2,969 |
1,114 |
1,853 |
2,309 |
3,181 |
1,336 |
2,154 |
2,663 |
3,638 | |||
|
25 |
0,842 |
1,496 |
1,895 |
2,647 |
0,999 |
1,702 |
2,132 |
2,952 |
1,103 |
1,838 |
2,292 |
3,158 |
1,319 |
2,129 |
2,632 |
3,601 | |||
|
30 |
0,825 |
1,475 |
1,869 |
2,613 |
0,966 |
1,657 |
2,080 |
2,884 |
1,059 |
1,778 |
2,220 |
3,064 |
1,249 |
2,029 |
2,516 |
3,446 | |||
|
35 |
0,812 |
1,458 |
1,849 |
2,588 |
0,942 |
1,623 |
2,041 |
2,833 |
1,025 |
1,732 |
2,166 |
2,994 |
1,195 |
1,957 |
2,431 |
3,334 | |||
|
40 |
0,803 |
1,445 |
1,834 |
2,568 |
0,923 |
1,598 |
2,010 |
2,793 |
0,999 |
1,697 |
2,126 |
2,941 |
1,154 |
1,902 |
2,365 |
3,250 | |||
|
45 |
0,795 |
1,435 |
1,821 |
2,552 |
0,908 |
1,577 |
1,986 |
2,762 |
0,978 |
1,669 |
2,092 |
2,897 |
1,122 |
1,857 |
2,313 |
3,181 | |||
|
50 |
0,788 |
1,426 |
1,811 |
2,538 |
0,894 |
1,560 |
1,965 |
2,735 |
0,961 |
1,646 |
2,065 |
2,863 |
1,096 |
1,821 |
2,296 |
3,124 | |||
=0,75_______________
* Соответствует оригиналу. - Примечание .
Примечание. Для 
50 
.
Таблица 74
Значения функции
|
|
|
|
-4,00 |
0,0001 |
|
-3,95 |
0,0002 |
|
-3,90 |
0,0002 |
|
-3,85 |
0,0002 |
|
-3,80 |
0,0003 |
|
-3,75 |
0,0004 |
|
-3,70 |
0,0004 |
|
-3,65 |
0,0005 |
|
-3,60 |
0,0006 |
|
-3,55 |
0,0007 |
|
-3,50 |
0,0009 |
|
-3,45 |
0,0010 |
|
-3,40 |
0,0012 |
|
-3,35 |
0,0015 |
|
-3,30 |
0,0017 |
|
-3,25 |
0,0020 |
|
-3,20 |
0,0024 |
|
-3,15 |
0,0028 |
|
-3,10 |
0,0033 |
|
-3,05 |
0,0038 |
|
-3,00 |
0,0044 |
|
-2,95 |
0,0052 |
|
-2,90 |
0,0060 |
|
-2,85 |
0,0069 |
|
-2,80 |
0,0079 |
|
-2,75 |
0,0091 |
|
-2,70 |
0,0105 |
|
-2,65 |
0,0120 |
|
-2,60 |
0,0136 |
|
-2,55 |
0,0155 |
|
-2,50 |
0,0176 |
|
-2,45 |
0,0200 |
|
-2,40 |
0,0226 |
|
-2,35 |
0,0255 |
|
-2,30 |
0,0286 |
|
-2,25 |
0,0321 |
|
-2,20 |
0,0360 |
|
-2,15 |
0,0402 |
|
-2,10 |
0,0448 |
|
-2,05 |
0,0498 |
|
-2,00 |
0,0552 |
|
-1,95 |
0,0612 |
|
-1,90 |
0,0676 |
|
-1,85 |
0,0745 |
|
-1,80 |
0,0819 |
|
-1,75 |
0,0899 |
|
-1,70 |
0,0984 |
|
-1,65 |
0,1076 |
|
-1,60 |
0,1174 |
|
-1,55 |
0,1277 |
|
-1,50 |
0,1388 |
|
-1,45 |
0,1505 |
|
-1,40 |
0,1629 |
|
-1,35 |
0,1760 |
|
-1,30 |
0,1897 |
|
-1,25 |
0,2042 |
|
-1,20 |
0,2194 |
|
-1,15 |
0,2354 |
|
-1,10 |
0,2520 |
|
-1,05 |
0,2694 |
|
-1,00 |
0,2876 |
|
-0,95 |
0,3065 |
|
-0,90 |
0,3261 |
|
-0,85 |
0,3465 |
|
-0,80 |
0,3676 |
|
-0,75 |
0,3894 |
|
-0,70 |
0,4119 |
|
-0,65 |
0,4352 |
|
-0,60 |
0,4591 |
|
-0,55 |
0,4838 |
|
-0,50 |
0,5092 |
|
-0,45 |
0,5352 |
|
-0,40 |
0,5619 |
|
-0,35 |
0,5892 |
|
-0,30 |
0,6172 |
|
-0,25 |
0,6458 |
|
-0,20 |
0,6751 |
|
-0,15 |
0,7049 |
|
-0,10 |
0,7353 |
|
-0,05 |
0,7663 |
|
0,00 |
0,7979 |
|
0,05 |
0,8300 |
|
0,10 |
0,8626 |
|
0,15 |
0,8958 |
|
0,20 |
0,9294 |
|
0,25 |
0,9636 |
|
0,30 |
0,9982 |
|
0,35 |
1,0332 |
|
0,40 |
1,0688 |
|
0,45 |
1,1047 |
|
0,50 |
1,1411 |
|
0,55 |
1,1779 |
|
0,60 |
1,2150 |
|
0,65 |
1,2526 |
|
0,70 |
1,2905 |
|
0,75 |
1,3288 |
|
0,80 |
1,3674 |
|
0,85 |
1,4064 |
|
0,90 |
1,4456 |
|
0,95 |
1,4852 |
|
1,00 |
1,5251 |
|
1,05 |
1,5653 |
|
1,10 |
1,6058 |
|
1,15 |
1,6465 |
|
1,20 |
1,6875 |
|
1,25 |
1,7288 |
|
1,30 |
1,7703 |
|
1,35 |
1,8121 |
|
1,40 |
1,8540 |
|
1,45 |
1,8963 |
|
1,50 |
1,9387 |
|
1,55 |
1,9813 |
|
1,60 |
2,0241 |
|
1,65 |
2,0672 |
|
1,70 |
2,1104 |
|
1,75 |
2,1538 |
|
1,80 |
2,1973 |
|
1,85 |
2,2410 |
|
1,90 |
2,2849 |
|
1,95 |
2,3290 |
|
2,00 |
2,3732 |
|
2,05 |
2,4176 |
|
2,10 |
2,4621 |
|
2,15 |
2,5067 |
|
2,20 |
2,5515 |
|
2,25 |
2,5964 |
|
2,30 |
2,6414 |
|
2,35 |
2,6866 |
|
2,40 |
2,7319 |
|
2,45 |
2,7773 |
|
2,50 |
2,8227 |
|
2,55 |
2,8684 |
|
2,60 |
2,9141 |
|
2,65 |
2,9598 |
|
2,70 |
3,0058 |
|
2,75 |
3,0519 |
|
2,80 |
3,0977 |
|
2,85 |
3,1441 |
|
2,90 |
3,1906 |
|
2,95 |
3,2366 |
|
3,00 |
3,2832 |
|
3,05 |
3,3311 |
|
3,10 |
3,3764 |
|
3,15 |
3,4244 |
|
3,20 |
3,4694 |
|
3,25 |
3,5180 |
|
3,30 |
3,5642 |
|
3,35 |
3,6121 |
|
3,40 |
3,6565 |
|
3,45 |
3,7069 |
|
3,50 |
3,7527 |
|
3,55 |
3,8002 |
|
3,60 |
3,8464 |
|
3,65 |
3,8964 |
|
3,70 |
3,9425 |
|
3,75 |
3,9924 |
|
3,80 |
4,0360 |
|
3,85 |
4,0891 |
|
3,90 |
4,1376 |
|
3,95 |
4,1842 |
|
4,00 |
4,2310 |
Таблица 75*
_______________
* Таблица приводится в соответствии с бумажным оригиналом. - Примечание .
Значения коэффициента 
|
|
| |||||||
|
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
4 |
3,428 |
|
|
|
|
|
|
|
|
5 |
4,444 |
|
|
|
|
|
|
|
|
6 |
5,454 |
4,864 |
|
|
|
|
|
|
|
7 |
6,461 |
5,887 |
|
|
|
|
|
|
|
8 |
7,466 |
6,904 |
6,303 |
|
|
|
|
|
|
9 |
8,470 |
7,916 |
7,330 |
|
|
|
|
|
|
10 |
9,473 |
8,925 |
8,351 |
7,744 |
|
|
|
|
|
11 |
10,476 |
9,933 |
9,367 |
8,773 |
|
|
|
|
|
12 |
11,478 |
10,939 |
10,380 |
9,797 |
9,185 |
|
|
|
|
13 |
12,480 |
11,944 |
11,390 |
10,816 |
10,216 |
|
|
|
|
14 |
13,481 |
12,948 |
12,399 |
11,831 |
11,242 |
10,626 |
|
|
|
15 |
14,482 |
13,952 |
13,406 |
12,844 |
12,263 |
11,659 |
|
|
|
16 |
15,483 |
14,955 |
14,413 |
13,856 |
13,281 |
12,686 |
12,068 |
|
|
17 |
16,484 |
15,958 |
15,419 |
14,865 |
14,296 |
13,709 |
13,102 |
|
|
18 |
17,485 |
16,960 |
16,424 |
15,874 |
15,310 |
14,729 |
14,130 |
13,510 |
|
19 |
18,486 |
17,962 |
17,428 |
16,881 |
16,321 |
15,747 |
15,155 |
14,544 |
|
20 |
19,487 |
18,964 |
18,432 |
17,888 |
17,332 |
16,762 |
16,177 |
15,574 |
|
21 |
20,487 |
19,966 |
19,435 |
18,894 |
18,341 |
17,775 |
17,195 |
16,600 |
|
22 |
21,488 |
20,968 |
20,438 |
19,899 |
19,349 |
18,787 |
18,212 |
17,623 |
|
23 |
22,488 |
21,969 |
21,441 |
20,904 |
20,356 |
19,798 |
19,227 |
18,643 |
|
24 |
23,489 |
22,970 |
22,444 |
21,908 |
21,363 |
20,808 |
20,241 |
19,662 |
|
25 |
24,489 |
23,972 |
23,446 |
22,912 |
22,369 |
21,817 |
21,253 |
20,678 |
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
26 |
21,110 |
20,515 |
19,905 |
19,279 |
|
|
|
|
|
27 |
22,128 |
21,537 |
20,934 |
20,315 |
|
|
|
|
|
28 |
23,144 |
22,558 |
21,960 |
21,348 |
20,722 |
|
|
|
|
29 |
24,159 |
23,577 |
22,984 |
22,378 |
21,758 |
|
|
|
|
30 |
25,173 |
24,594 |
24,005 |
23,405 |
22,791 |
22,164 |
|
|
|
31 |
26,185 |
25,610 |
25,025 |
24,429 |
23,821 |
23,201 |
|
|
|
32 |
27,197 |
26,625 |
26,044 |
25,452 |
24,849 |
24,234 |
23,606 |
|
|
33 |
28,208 |
27,639 |
27,061 |
26,473 |
25,875 |
25,265 |
24,643 |
|
|
34 |
29,218 |
28,651 |
28,076 |
27,492 |
26,898 |
26,294 |
25,677 |
25,049 |
|
35 |
30,227 |
29,663 |
29,091 |
28,510 |
27,920 |
27,320 |
26,709 |
26,086 |
|
36 |
31,236 |
30,674 |
30,105 |
29,527 |
28,940 |
28,344 |
27,738 |
27,121 |
|
37 |
32,244 |
31,685 |
31,118 |
30,543 |
29,959 |
29,367 |
28,765 |
28,152 |
|
38 |
33,252 |
32,694 |
32,130 |
31,557 |
30,977 |
30,388 |
29,790 |
29,182 |
|
39 |
34,259 |
33,703 |
33,141 |
32,571 |
31,993 |
31,408 |
30,813 |
30,209 |
|
40 |
35,266 |
34,712 |
34,151 |
33,584 |
33,009 |
32,426 |
31,835 |
31,235 |
|
41 |
36,272 |
35,720 |
35,161 |
34,596 |
34,023 |
33,443 |
32,855 |
32,259 |
|
42 |
37,278 |
36,728 |
36,171 |
35,607 |
35,037 |
34,460 |
33,875 |
33,282 |
|
43 |
38,284 |
37,735 |
37,180 |
36,618 |
36,050 |
35,475 |
34,893 |
34,303 |
|
44 |
39,290 |
38,742 |
38,188 |
37,628 |
37,062 |
36,489 |
35,910 |
35,323 |
|
45 |
40,295 |
39,748 |
39,196 |
38,638 |
38,074 |
37,503 |
36,926 |
36,342 |
|
46 |
41,300 |
40,754 |
40,204 |
39,647 |
39,085 |
38,516 |
37,941 |
37,359 |
|
47 |
42,305 |
41,760 |
41,211 |
40,656 |
40,095 |
39,528 |
38,956 |
38,376 |
|
48 |
43,309 |
42,766 |
42,218 |
41,664 |
41,105 |
40,540 |
39,969 |
39,392 |
|
49 |
44,314 |
43,771 |
43,224 |
42,672 |
42,114 |
41,551 |
40,982 |
40,407 |
|
50 |
45,318 |
44,776 |
44,230 |
43,679 |
43,123 |
42,562 |
41,995 |
41,422 |
|
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
26 |
25,490 |
24,973 |
24,448 |
23,916 |
23,375 |
22,825 |
22,264 |
21,693 |
|
27 |
26,490 |
25,974 |
25,450 |
24,919 |
24,380 |
23,832 |
23,274 |
22,707 |
|
28 |
27,490 |
26,975 |
26,452 |
25,922 |
25,385 |
24,389* |
24,284 |
23,719 |
|
_______________ | ||||||||
|
29 |
28,491 |
27,976 |
27,454 |
26,925 |
26,399 |
25,845 |
25,292 |
24,731 |
|
30 |
29,491 |
28,977 |
28,456 |
27,928 |
27,393 |
26,851 |
26,300 |
25,741 |
|
31 |
30,491 |
29,977 |
29,457 |
28,930 |
28,397 |
27,856 |
27,308 |
26,751 |
|
32 |
31,492 |
30,978 |
30,458 |
29,933 |
29,400 |
28,861 |
28,314 |
27,760 |
|
33 |
32,492 |
31,979 |
31,460 |
30,935 |
30,404 |
29,866 |
29,321 |
28,768 |
|
34 |
33,492 |
32,979 |
32,461 |
31,937 |
31,407 |
30,870 |
30,327 |
29,776 |
|
35 |
34,492 |
33,980 |
33,462 |
32,939 |
32,410 |
31,874 |
31,332 |
30,783 |
|
36 |
35,492 |
34,980 |
34,463 |
33,941 |
33,412 |
32,878 |
32,337 |
31,790 |
|
37 |
36,493 |
35,981 |
35,464 |
34,942 |
34,415 |
33,882 |
33,342 |
32,797 |
|
38 |
37,493 |
36,981 |
36,465 |
35,944 |
35,417 |
34,885 |
34,347 |
33,803 |
|
39 |
38,493 |
37,982 |
37,466 |
36,945 |
36,419 |
35,888 |
35,351 |
34,808 |
|
40 |
39,493 |
38,982 |
38,467 |
37,947 |
37,422 |
36,891 |
36,355 |
35,814 |
|
41 |
40,493 |
39,983 |
39,468 |
38,948 |
38,424 |
37,894 |
37,359 |
36,819 |
|
42 |
41,493 |
40,983 |
40,469 |
39,949 |
39,426 |
38,897 |
38,363 |
37,823 |
|
43 |
42,494 |
41,984 |
41,469 |
40,951 |
40,427 |
39,899 |
39,366 |
38,828 |
|
44 |
43,494 |
42,984 |
42,470 |
41,952 |
41,429 |
40,902 |
40,370 |
39,832 |
|
45 |
44,494 |
43,984 |
43,471 |
42,953 |
42,431 |
41,904 |
41,373 |
40,836 |
|
46 |
45,494 |
44,985 |
44,471 |
43,954 |
43,432 |
42,906 |
42,376 |
41,840 |
|
47 |
46,494 |
45,985 |
45,472 |
44,955 |
44,434 |
43,908 |
43,379 |
42,844 |
|
48 |
47,494 |
46,985 |
46,473 |
45,956 |
45,435 |
44,910 |
44,381 |
43,848 |
|
49 |
48,494 |
47,986 |
47,473 |
46,957 |
46,437 |
45,912 |
45,384 |
44,851 |
|
50 |
49,494 |
48,986 |
48,474 |
47,958 |
47,438 |
46,914 |
46,386 |
45,854 |
Примечание.
или
Таблица 76
Значения 
и
|
|
|
|
|
0,10 |
0,957 |
11,65 |
|
0,15 |
0,941 |
7,92 |
|
0,20 |
0,927 |
6,00 |
|
0,25 |
0,913 |
4,50 |
|
0,30 |
0,903 |
3,68 |
ПРИЛОЖЕНИЕ 10
Справочное
ПРИМЕРЫ ПЛАНИРОВАНИЯ ИСПЫТАНИЙ И ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
ПО РЕЗУЛЬТАТАМ ИСПЫТАНИЙ
Пример 1. Для плана испытаний определить число объектов испытаний, чтобы с доверительной вероятностью =0,90 предельная относительная ошибка в определении среднего ресурса не превышала 0,10. Предполагается, что ресурс распределен нормально с коэффициентом вариации =0,20.
Решение. В соответствии с п.1.1 приложения 4 по табл.5 для =0,90; =0,10; =0,20 находим =8.
По результатам испытаний 8 объектов получен коэффициент вариации 
=0,25.
В соответствии с п.1.3 приложения 4 определяем дополнительное число объектов, которые необходимо поставить на испытание. Для =0,90; =0,10; =0,25 по табл.5 находим =12. Следовательно, на испытания необходимо дополнительно поставить 4 объекта.
По результатам испытаний 12 объектов получен коэффициент вариации 
=0,23. Так как <0,25, то перепланирование не требуется.
Пример 2. Для плана испытаний определить число объектов испытаний, чтобы с доверительной вероятностью =0,80 предельная относительная ошибка в определении средней наработки до отказа для объема совокупности , равного 40, не превышала 0,15. Предполагается, что наработка до отказа имеет распределение Вейбулла с коэффициентом вариации =0,5.
Решение. В соответствии с п.1.1 приложения 4 по табл.17 (=40) для =0,80; =0,15; =0,5 находим =3.
По результатам испытаний 3 объектов получен коэффициент вариации =0,4. Перепланирование не требуется.
Пример 3. Для плана испытаний определить число объектов испытаний, чтобы с доверительной вероятностью =0,80 предельная относительная ошибка в определении 90%-ного ресурса не превышала 0,20. Предполагается, что распределение ресурса логарифмически нормальное с коэффициентом вариации =0,4, относительная продолжительность испытаний =0,9.
Решение. В соответствии с п.2.3 приложения 4 по табл.25 для
;
=0,80; =0,20 и =0,4 находим число предельных состояний, равное 8.
В соответствии с п.2.4 приложения 4 находим объем выборки из условия =0,9; значение находим по табл.60 приложения 9.
.
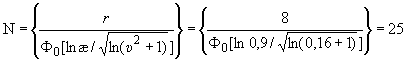Пример 4. Для плана испытаний определить число объектов испытаний, чтобы с доверительной вероятностью =0,90 предельная относительная ошибка в определении средней наработки до отказа не превышала 0,20. Предполагается, что распределение наработки до отказа нормальное с коэффициентом вариации, равным 0,20, относительная продолжительность испытаний =1.
Решение. В соответствии с п.3.1 приложения 4 по табл.5 для =0,90; =0,20, =0,20 находим прогнозируемое число отказов , равное 4. Для найденного значения определяем объем выборки по формуле п.2.2 приложения 3 из условия =1.
.
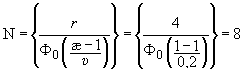Пример 5. Для плана испытаний определить число объектов испытаний, чтобы с доверительной вероятностью =0,80 определить 90%-ный ресурс объектов. Установленное число предельных состояний равно 20.
Решение. В соответствии с п.2.6 приложения 4 по табл.26 для =0,80;
и =20 находим =200.
Пример 6. Для плана испытаний определить число объектов испытаний, чтобы с доверительной вероятностью =0,8 предельная относительная ошибка в определении средней наработки на отказ не превышала 0,2. Предполагается, что наработка между отказами распределяется экспоненциально.
Решение. В соответствии с п.4.3 приложения 4 по табл.27 для =0,8 и =0,2 определим прогнозируемое число отказов , равное 29. Объем выборки находим, полагая =2:
.
Для =0,5 объем выборки равен
.
Пример 7. Для плана определить число отказов, чтобы с доверительной вероятностью =0,8 предельная относительная ошибка в определении коэффициента готовности не превышала 0,10. Коэффициент вариации наработки между отказами равен 0,4, коэффициент вариации времени восстановления равен 0,6.
Решение. В соответствии с п.42 приложения 4 по табл.33 находим =0,8; =0,1; =0,4; 
=0,6 находим =40.
Пример 8. Для плана определить объем выборки , чтобы с доверительной вероятностью =0,9 предельная относительная ошибка в оценке средней наработки до отказа не превышала =0,15. Коэффициент вариации равен 0,6. Закон распределения наработки до отказа неизвестен.
Решение. В соответствии с п.5 приложения 4 находим объем выборки для случаев, когда распределения наработки до отказа являются Вейбулловски и логарифмически нормальными. В соответствии с п.1.1 приложения 4 по табл.6 и табл.8 находим =32 и =25.
Таким образом, объем выборки равен 32.
Пример 9. Определить объем выборки при биноминальных испытаниях для оценки нижней доверительной границы вероятности безотказной работы 
за наработку с доверительной вероятностью =0,80 при допустимом числе отказавших изделий =5. Ожидаемое значение =0,80.
Решение. В соответствии с п.3.5 приложения 4 объем выборки определяют по табл.28.
Для =0,80; =0,80 и =5 объем выборки =38.
Пример 10. По результатам испытаний по плану 
получены следующие исходные данные для оценки показателей надежности:
10 выборочных значений наработки до отказа (тыс. км): 25; 59; 61; 65; 79; 98; 109; 118; 153; 195;
10 выборочных значений наработки до цензурирования 
(10 изделий остались в работоспособном состоянии к моменту окончания испытаний): 36; 48; 71; 85; 88; 102; 129; 138; 156; 200.
Определить точечные оценки средней наработки до отказа , вероятности безотказной работы за 72 ч 
и с доверительной вероятностью =0,8 нижние доверительные границы 
и 
.
Решение. В соответствии с п.1.2 приложения 5 наработки до отказа и наработки до цензурирования выстраивают в общий вариационный ряд в порядке неубывания наработок (наработки до цензурирования помечены *): 25; 36*; 48*; 52; 61; 65; 71*; 79; 85*; 88*; 98; 102*; 109; 118; 129*; 138*; 153; 156*; 195; 200*.
В соответствии с п.1.2 приложения 5 вычисляют оценку функции распределения 
:
;
;
;
;
.
Аналогично подсчитывают:
;
_______________
* Соответствует оригиналу. - Примечание .
;
;
;
.
По формулам табл.36 вычисляют точечные оценки и 
:
.
Здесь
.
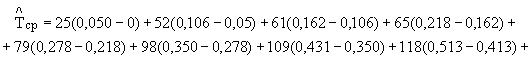
(тыс. км).
,
где 
;
.
По формулам табл.37 вычисляют нижнюю доверительную границу для средней наработки до отказа:
(тыс. км).
По формулам табл.37 вычисляют нижнюю доверительную границу для вероятности безотказной работы:
;
;
;
.
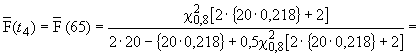
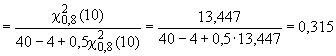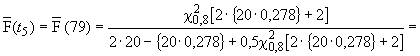
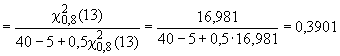Пример 11. По результатам испытаний по плану получены следующие данные для оценки показателей надежности (основная экспериментальная информация): 5 выборочных значений наработки до отказа: 1,96; 2,92; 6,45; 8,84; 9,95 (час); 5 выборочных значений наработки до цензурирования: 1,78; 2,03; 9,21; 11,24; 16,9 (час).
Определить точечные и интервальные оценки средней наработки до отказа 
. Наработка до отказа подчиняется распределению Вейбулла.
Решение. Вычисления проводим в соответствии с п.1 приложения 7.
Вычисляем точечные оценки параметров распределения в соответствии с приложением в следующей последовательности (=0,01):
Вычисляют коэффициент :
;
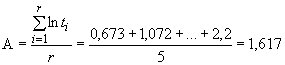вычисляют начальное приближение 
:
;
вычисляют 1-е приближение 
:
Аналогично вычисляют
=1,39; 
=1,44; 
=1,41; 
=1,42.
Так как 
=0,007<0,01, то в качестве оценки параметра следует принять 
.
Вычисляют оценку параметра :
.
Вычисляют точечную оценку средней наработки до отказа по формуле табл.38 приложения 5:
.
Вычисляют нижнюю одностороннюю границу средней наработки до отказа по формуле табл.48 приложения 5.
Значение определяют по табл.65 приложения 8 для
и 
.
.
.
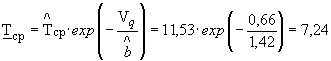Пример 12. По результатам испытаний по плану определить точечные и интервальные оценки с доверительной вероятностью =0,9 средней наработки до отказа и 90%-ной наработки до отказа. Исходные данные - по примepy 11.
Наработка до отказа подчиняется нормальному распределению.
Решение. Вычисление проводим в соответствии с п.2.2 приложения 5.
Вычисляем точечные оценки параметров в соответствии с приложением 7 в следующей последовательности. (Точность решения уравнений 
).
Уравнения для вычисления оценок 
и 
имеют вид:
;
.
Здесь 
;
;
;
;
.
Для вычисления первого приближения 
и 
необходимо определить остаточный член 
линейного разложения 
:
.
После подстановки значений 
, 
получаем (индекс при 
опущен):
.
Аналогично вычисляем:
;
;
;
.
Вычисляем
;
.
Подставляя полученные значения в уравнение относительно , находим:
;
.
Проверяем достигнута ли требуемая точность
;
.
Следовательно, точечные оценки и равны: =10,4; =6,44.
Необходимо подчеркнуть, что истинные (смоделированные) значения параметров были равны =10, =6,78.
Вычисляют точечную и интервальную (нижнюю доверительную границу) оценки средней наработки до отказа и 
по формулам из табл.38, 51:
(ч);
(ч).
Квантиль распределения Стьюдента 
определяют по табл.72.
Вычисляют точечную и интервальную (нижнюю доверительную границу) 90% наработки до отказа 
и 
по формулам из табл.38, 51:
(ч);
.
Следовательно, =0.
Значение 
определяют из табл.66.
Значение 
определяют по табл.73.
Пример 13. По результатам испытаний 10 восстанавливаемых изделий вычислить оценку средней наработки на отказ 
. Испытания проводились по плану в течение =1000 ч, при этом было зафиксировано 6 отказов. Распределение наработки между отказами неизвестно.
Решение. В соответствии с п.1.3 приложения 5 определяют суммарную наработку 10 изделий за время испытаний:
(ч).
Вычисляют точечную оценку средней наработки на отказ:
(ч).
Вычисляют нижнюю доверительную границу средней наработки на отказ при доверительной вероятности =0,8 по формулам табл.46, 47:
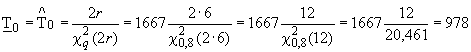(ч).
Пример 14. По результатам примера 13 вычислить оценку средней наработки на отказ, если за время испытаний отказов не наблюдалось.
Решение. Вычисляют нижнюю доверительную границу наработки на отказ по формулам табл.46 и 47, значение 
определяют по табл.66
(ч).
Пример 15. Определить точечную оценку и нижнюю доверительную границу вероятности безотказной работы технического объекта за 100 (ч). Структурная схема надежности объекта представлена на черт.10. Доверительная вероятность =0,8.
Черт.10
Одинаковыми цифрами обозначены однотипные составные части.
Испытания объекта проводились по плану , =3, =300 ч.
Закон распределения наработок до отказа элементов объекта - экспоненциальный. Результаты испытаний объекта представлены в табл.77.
Таблица 77
Результаты испытаний объекта
|
Номер объекта |
Наработки до отказа в часах | ||
|
|
элемента первого типа |
элемента второго типа |
объекта в целом |
|
1 |
250 |
- |
250 |
|
2 |
- |
150, 280 |
280 |
|
3 |
- |
250, 300 |
300 |
В качестве дополнительной информации о надежности элементов первого типа используют результаты автономных испытаний элемента в ужесточенном режиме.
За время испытаний произошло 3 отказа. Наработки отказавших элементов составили 100, 350, 200 (ч).
Отношение средних наработок до отказа в автономных и системных испытаниях элемента первого типа имеет вид:
.
В качестве дополнительной информации о надежности элементов второго типа используются результаты автономных испытаний элемента-прототипа. Испытания проводились по плану , =8, =400. Заведомо известно, что надежность прототипа не превосходит надежности элемента второго типа.
Решение. Объединенные (с использованием дополнительной информации) оценки показателей надежности элемента первого типа получают по формулам приложения 7 в условиях ТС-2*:
; 
;
;
;
.
________________
* Здесь и далее первый индекс соответствует типу элемента.
Объединенные оценки показателей надежности элементов второго типа получают по формулам приложения 7 в условиях ТС-4. При этом вначале получают точечные оценки средней наработки до отказа по основным и дополнительным данным:
;
.
Поскольку 
, объединенная точечная оценка средней наработки до отказа вычисляется следующим образом:
.
Тогда
.
В соответствии с методами приложения 7 в условиях ТС-4 для определения нижней доверительной границы элемента второго типа, соответствующей доверительной вероятности =0,8 определяют нижние доверительные границы по основной и дополнительной информации отдельно с доверительной вероятностью
.
В соответствии с приложением 5 вычисляют нижние доверительные границы для вероятности безотказной работы для экспоненциального распределения
.
Таким образом, объединенная интервальная оценка вероятности безотказной работы элемента второго типа, соответствующая доверительной вероятности 0,80, равна
.
В соответствии со структурной схемой надежности функция связи вероятности безотказной работы объекта с вероятностями безотказной работы элементов имеет вид:
,
поэтому объединенная точечная оценка вероятности безотказной работы объекта имеет вид:
.
Интервальная оценка вероятности безотказной работы объекта определяется в соответствии с приложением 5 методом подстановки:
.
Пример 16. Определить нижнюю доверительную границу вероятности безотказной работы 
за наработку с доверительной вероятностью =0,90. При биноминальных испытаниях (по плану ) =20 изделий зафиксировано 2 отказа.
Решение. В соответствии с п.2.1 приложения 8 нижняя доверительная граница вероятности безотказной работы за наработку равна:
.
Текст документа сверен по:
/ Госстандарт СССР. -
М.: Издательство стандартов, 1990
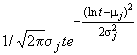
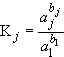
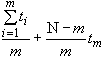
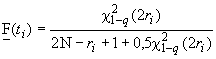
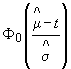
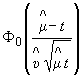
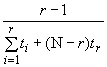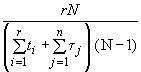
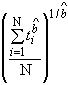
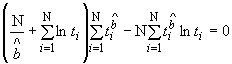
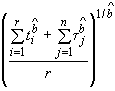
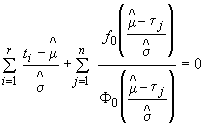
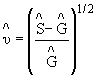
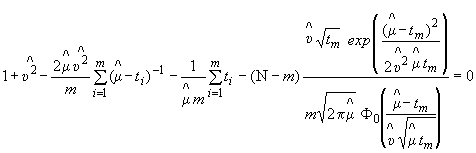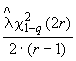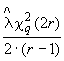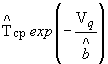
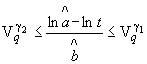
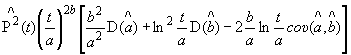
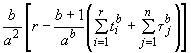