- USD ЦБ 03.12 30.8099 -0.0387
- EUR ЦБ 03.12 41.4824 -0.0244
|
Краснодар:
|
погода |
Курсы
Индексы
- DJIA 03.12 12019.4 -0.01
- NASD 03.12 2626.93 0.03
- RTS 03.12 1545.57 -0.07
Р 50.1.061-2007
Группа Т59
РЕКОМЕНДАЦИИ ПО СТАНДАРТИЗАЦИИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
ПРАКТИЧЕСКОЕ РУКОВОДСТВО ПО ИСПОЛЬЗОВАНИЮ
ГОСТ Р ИСО 5725-2-2002 ПРИ ПЛАНИРОВАНИИ, ВЫПОЛНЕНИИ
И СТАТИСТИЧЕСКОМ АНАЛИЗЕ МЕЖЛАБОРАТОРНОЙ ПОВТОРЯЕМОСТИ
И ВОСПРОИЗВОДИМОСТИ РЕЗУЛЬТАТОВ
Statistical methods.
Practical guidance for the use of GOST R ISO 5725-2-2002 in designing,
implementing and statistically analyzing interlaboratory repeatability
and reproducibility results
ОКС 03.120.30
Дата введения 2007-11-01
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. N 184-ФЗ "О техническом регулировании", а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 "Стандартизация в Российской Федерации. Основные положения"
Сведения о рекомендациях
1 ПОДГОТОВЛЕНЫ Открытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (ОАО НИЦ КД) и Техническим комитетом по стандартизации ТК 125 "Статистические методы в управлении качеством продукции" на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2 ВНЕСЕНЫ Управлением развития, информационного обеспечения и аккредитации Федерального агентства по техническому регулированию и метрологии
3 УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 7 июня 2007 г. N 120-ст
4 Настоящие рекомендации являются идентичными по отношению к документу ИСО/ТО 22971:2005 "Точность, правильность и прецизионность методов и результатов измерений. Практическое руководство по использованию ИСО 5725-2:1994 при планировании, выполнении и статистическом анализе межлабораторной повторяемости и воспроизводимости результатов" (ISO/TR 22971:2005 "Accuracy (trueness and precision) of measurement methods and results - Practical guidance for the use of ISO 5725-2:1994 in designing, implementing and statistically analysing interlaboratory repeatability and reproducibility results").
Наименование настоящих рекомендаций изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении А
5 ВВЕДЕНЫ ВПЕРВЫЕ
Информация об изменениях к настоящим рекомендациям и текст изменений и поправок публикуются в ежемесячно издаваемых информационных указателях "Национальные стандарты". В случае пересмотра (замены) или отмены настоящих рекомендаций соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте национального органа в сети Интернет
Введение
Серия стандартов ИСО 5725 состоит из шести частей, общая структура которых показана на рисунке 1.
ИСО 5725-2 [2] был разработан как руководство для технических комитетов и других организаций, ответственных за проведение межлабораторных исследований для оценки изменчивости, соответствующей стандартным методам измерений. Такие меры изменчивости, как повторяемость и воспроизводимость, приняты во многих дисциплинах как характеристики данных, с которыми сталкиваются при измерениях.
Повторяемость характеризует изменчивость измерений, выполняемых на идентичных образцах или материалах в идентичных условиях. Очевидно, что из-за неизвестных или не поддающихся контролю факторов, которые влияют на процесс измерений, повторные измерения обычно не совпадают с первоначальными. Степень этой изменчивости может быть выражена стандартным отклонением, названным внутрилабораторным стандартным отклонением повторяемости результатов.
Воспроизводимость характеризует изменчивость измерений, сделанных на идентичных образцах или материалах в отличающихся условиях различными лабораториями одним и тем же стандартным методом измерений. Воспроизводимость включает в себя воздействия, вызванные различиями инструментов, реактивов, операторов, лабораторий и экологических условий. Изменчивость результатов в этих условиях может быть описана стандартным отклонением, названным стандартным отклонением воспроизводимости.
Настоящее руководство включает в себя четыре основных раздела.
Раздел 2 включает в себя описание организации межлабораторной программы, относится к организации межлабораторных испытаний и касается роли ответственного исполнителя, лабораторного персонала и статистика при подготовке и управлении испытаниями, выбора материалов и уровней исследования для испытаний и выбора лабораторий. Руководство также описывает, какое количество повторных измерений (выполняемых на каждом образце) необходимо статистически обработать, и способ регистрации результатов.
Раздел 3 описывает экспертизу с помощью графических и вычислительных процедур. Даются рекомендации по выделению аномальных данных, то есть данных, противоречащих другим данным, и для независимых тестов для идентификации наличия и отсутствия аномальных данных.
Раздел 4 включает в себя методы оценки повторяемости и стандартного отклонения повторяемости, описывает интерпретацию повторяемости и стандартного отклонения повторяемости. Раздел также включает в себя сравнение относительных вкладов стандартных отклонений повторяемости и воспроизводимости в полную изменчивость метода испытаний.
Раздел 5 включает в себя примеры обработки, использующие программное обеспечение по статистическим методам, и обработанные примеры, в которых рассмотрены различные методы.
Рекомендуется изучать настоящее руководство вместе с ИСО 5725-2 [2], но не использовать его вместо ИСО 5725-2.
1 Область применения
Настоящие рекомендации являются руководством по использованию ИСО 5725-2 (см. [2]) и содержат упрощенные последовательные процедуры для планирования, выполнения и статистического анализа межлабораторных исследований для оценки изменчивости стандартного метода измерений и определения повторяемости и воспроизводимости данных, полученных при межлабораторных испытаниях.
2 Организация межлабораторной программы
2.1 Требования к прецизионности эксперимента
Эксперимент проводят чтобы:
a) обеспечить полный набор результатов для:
- определения количества лабораторий ![]() , необходимых для демонстрации того, что их процедура испытаний хорошо контролируется, и для определения количественной оценки наблюдаемых рассеяний, характеризуемых воспроизводимостью;
, необходимых для демонстрации того, что их процедура испытаний хорошо контролируется, и для определения количественной оценки наблюдаемых рассеяний, характеризуемых воспроизводимостью;
Примечание - Символ ![]() , используемый в настоящих рекомендациях, имеет тот же смысл, что и символ
, используемый в настоящих рекомендациях, имеет тот же смысл, что и символ ![]() , используемый в ИСО 5725-2 (см. [2]). Замена символа была сделана, чтобы четко отличать этот символ от символа
, используемый в ИСО 5725-2 (см. [2]). Замена символа была сделана, чтобы четко отличать этот символ от символа ![]() , используемого для обозначения вероятности.
, используемого для обозначения вероятности.
- определения количества образцов или продукции ![]() , необходимых для представления различных уровней результатов или параметра. Минимальное значение
, необходимых для представления различных уровней результатов или параметра. Минимальное значение ![]() - два, но для демонстрации того, что процедура испытаний способна правильно различать уровни, более подходящими являются значения от пяти до десяти;
- два, но для демонстрации того, что процедура испытаний способна правильно различать уровни, более подходящими являются значения от пяти до десяти;
- определения количества базовых элементов ![]() , демонстрирующих, что процедура испытаний хорошо контролируется в пределах единственной лаборатории. Когда количество лабораторий и уровней является достаточным, требуется по крайней мере два определения;
, демонстрирующих, что процедура испытаний хорошо контролируется в пределах единственной лаборатории. Когда количество лабораторий и уровней является достаточным, требуется по крайней мере два определения;
b) статистически анализировать (см. разделы 2 и 3) таблицу результатов, зафиксированных ![]() лабораториями, анализирующими
лабораториями, анализирующими ![]() образцов, испытанных
образцов, испытанных ![]() раз в условиях повторяемости.
раз в условиях повторяемости.
Таблица результатов, предоставляемых ответственному исполнителю, показана в таблице 1 (см. ИСО 5725-2 [2], 7.2.8).
2.2 Обязанности персонала, вовлеченного в эксперимент на прецизионность
2.2.1 Общие положения
Межлабораторная программа является очень дорогой как в отношении ее координации, так и в отношении участия в этой программе. Следовательно, выполнение испытаний должно быть хорошо скоординировано и спланировано. В любой межлабораторной программе необходимо рассмотреть три типа деятельности, показанных на рисунке 2.
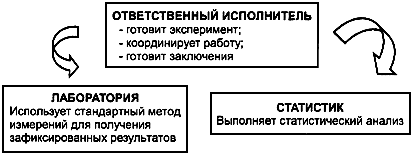
Рисунок 2 - Обязанности и функции исполнителей
2.2.2 Ответственный исполнитель
Главные задачи ответственного исполнителя:
- организация межлабораторной программы с участием статистика при разработке плана эксперимента;
- координация выполнения программы;
- формирование заключений.
Обязанности ответственного исполнителя могут выполнять несколько человек. Однако только один человек должен нести ответственность за программу в целом. Ответственный исполнитель должен быть знаком со стандартным методом, но не должен участвовать в процессе измерений.
2.2.3 Лаборатория
Лабораторный персонал должен быть хорошо знаком с исследуемым методом измерений.
Лаборатория должна выполнять анализ, придерживаясь процедуры испытаний, полученной от ответственного исполнителя. Любые комментарии лаборатории по использованию исследуемого метода необходимо сообщать ответственному исполнителю. Однако процедуры, выполненные лабораторией, должны быть обеспечены ответственным исполнителем.
Лаборатория должна выполнять любые требования, предписанные ответственным исполнителем, включая:
- хранение образцов;
- время и порядок выполнения анализа.
Лаборатория должна обеспечивать ответственного исполнителя результатами анализа в соответствии с установленным им способом.
2.2.4 Статистик
Статистик должен получать от ответственного исполнителя необработанные данные, полученные с использованием заявленного метода и представленные в соответствии с таблицей 1.
Статистик должен исследовать данные и применять любой статистический критерий, предпочтительно критерий, описанный в ИСО 5725-2 [2], для идентификации потенциальных выбросов. Статистические выбросы должны быть представлены ответственному исполнителю. Ответственный исполнитель должен предпринимать необходимые исследования и принимать решение о сохранении, отклонении или изменении каких-либо данных.
Статистик должен выполнять статистический анализ, подготавливать графики и рассчитывать оценки среднего и дисперсий (ИСО 5725-2 [2], 7.1.2). Статистик должен суммировать все результаты статистического анализа в отчете, который направляют ответственному исполнителю.
3 Критическая экспертиза данных
3.1 Описание данных
3.1.1 Необработанные данные
Данные представляют в соответствии с таблицей 1. Таблицы 2 и 3 получают из таблицы 1. Некоторые статистические пакеты программ обеспечивают другое представление той же самой информации.
Таблица 1 - Сопоставление всех необработанных данных
|
Лаборатория |
Уровень | ||||||
|
|
1 |
2 |
… |
|
… |
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 - Сопоставление выборочных средних для каждого базового элемента таблицы 1
|
Лаборатория |
Уровень | ||||||
|
|
1 |
2 |
… |
|
… |
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3 - Сопоставление величин, характеризующих разброс![]() для каждого базового элемента таблицы 1
для каждого базового элемента таблицы 1
|
Лаборатория |
Уровень | ||||||
|
|
1 |
2 |
… |
|
… |
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
3.1.2 Графическое представление данных
3.1.2.1 График данных лаборатории (необработанные данные)
Перед выполнением любых тестов для определения потенциальных выбросов рекомендуется делать графическое отображение необработанных данных. Этот способ позволяет получать наглядную картину результатов, например, как показано на рисунке 3 (который основан на рисунках В.1-В.4 ИСО 5725-2 [2]). В результате визуального анализа графического отображения необработанных данных можно получать много информации и устанавливать мгновенную оценку разброса данных. Следовательно, можно сделать предположения о наличии выбросов или можно выявлять необычные различия в конкретных уровнях исследования простым визуальным осмотром соответствующего графического отображения данных. Например, на рисунке 3 по отображению данных лаборатории 3 можно предположить больший, чем ожидалось, разброс результатов по сравнению со всеми другими лабораториями. Следовательно, это может влиять на полную повторяемость. Эти предположения можно проверить с помощью критерия Кохрена. Кроме того, по результатам лаборатории 9 можно предположить существенное отклонение выборочного среднего лаборатории по сравнению с выборочными средними других лабораторий. Следовательно, это может влиять на воспроизводимость и это можно подтвердить критерием Граббса.

Обозначения:
![]() - номер лаборатории;
- номер лаборатории;
![]() - результаты лаборатории
- результаты лаборатории
Рисунок 3 - Графическое представление необработанных данных
для конкретного уровня исследований
3.1.2.2 График "квадратики и усики"
Когда известно много результатов, особенно для конкретного уровня исследований, график "квадратики и усики" может показывать информацию аналогично 3.1.2.1, например см. рисунок 4. Однако этот тип графика, основанный на робастных методах статистики, включая определение значения медианы, не описан в ИСО 5725-2 [2]. Он определен и иллюстрирован в примерах раздела 4, так как эти графики имеются в большинстве статистических пакетов программ.
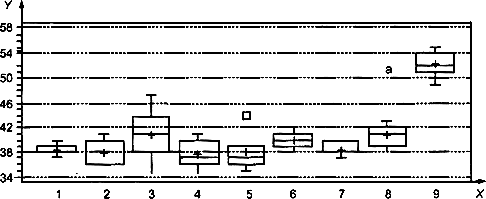
Обозначения:
![]() - номер лаборатории;
- номер лаборатории;
![]() - результаты лаборатории;
- результаты лаборатории;
"+" - обозначение выборочного среднего
Рисунок 4 - График "квадратики и усики"
3.1.2.3 Графики ![]() и
и ![]() тестовых статистик Манделя
тестовых статистик Манделя
3.1.2.3.1 График ![]() -статистики Манделя
-статистики Манделя
Для конкретного исследуемого уровня выборочные средние, полученные для всех лабораторий, используют для вычисления единственного общего выборочного среднего. Это значение затем используют для вычисления ![]() -статистики Манделя всех лабораторий этого уровня. Эта статистика определена в ИСО 5725-2 [2], уравнение (6), и представляет собой отношение разности среднего для конкретного набора данных и среднего всех наборов данных и стандартного отклонения средних по всем наборам данных. Это значение затем наносят на график и сравнивают с вычисленными или табулированными значениями отношения для 95% и 99% уровней доверия. Затем ту же процедуру используют для вычисления
-статистики Манделя всех лабораторий этого уровня. Эта статистика определена в ИСО 5725-2 [2], уравнение (6), и представляет собой отношение разности среднего для конкретного набора данных и среднего всех наборов данных и стандартного отклонения средних по всем наборам данных. Это значение затем наносят на график и сравнивают с вычисленными или табулированными значениями отношения для 95% и 99% уровней доверия. Затем ту же процедуру используют для вычисления ![]() -статистики Манделя для всех лабораторий всех других уровней (см. рисунок 5). Необходимо отметить, что могут быть получены положительные и отрицательные значения.
-статистики Манделя для всех лабораторий всех других уровней (см. рисунок 5). Необходимо отметить, что могут быть получены положительные и отрицательные значения.

Обозначения:
![]() - номер лаборатории;
- номер лаборатории;
![]() -
- ![]() -статистика Манделя;
-статистика Манделя;
![]() - уровень доверия 99%;
- уровень доверия 99%;
![]() - уровень доверия 95%
- уровень доверия 95%
Рисунок 5 - График ![]() -статистик Манделя
-статистик Манделя
3.1.2.3.2 График ![]() -статистики Манделя
-статистики Манделя
Для конкретного исследуемого уровня стандартные отклонения, полученные для всех лабораторий, используют для вычисления среднего стандартного отклонения или объединенного единственного стандартного отклонения. Это значение затем используют для вычисления ![]() -статистики Манделя для всех лабораторий этого уровня. Эта статистика определена в ИСО 5725-2 [2], уравнение (7), и представляет собой отношение стандартного отклонения результатов к среднему или объединенному стандартному отклонению. Это значение отношения затем наносят на график и сравнивают с вычисленными или табличными значениями отношения, полученными для 95% и 99% уровней доверия. Затем ту же процедуру используют для вычисления
-статистики Манделя для всех лабораторий этого уровня. Эта статистика определена в ИСО 5725-2 [2], уравнение (7), и представляет собой отношение стандартного отклонения результатов к среднему или объединенному стандартному отклонению. Это значение отношения затем наносят на график и сравнивают с вычисленными или табличными значениями отношения, полученными для 95% и 99% уровней доверия. Затем ту же процедуру используют для вычисления ![]() -статистики Манделя для всех лабораторий всех других исследуемых уровней (см. рисунок 6). Необходимо отметить, что могут быть получены только положительные значения.
-статистики Манделя для всех лабораторий всех других исследуемых уровней (см. рисунок 6). Необходимо отметить, что могут быть получены только положительные значения.
3.1.2.3.3 Графический контроль
По графику можно идентифицировать результаты каждой лаборатории, которые можно рассматривать отличными от ожидаемого распределения результатов. Например, график ![]() для конкретных исследуемых уровней каждой лаборатории мог бы приближать или превышать значение
для конкретных исследуемых уровней каждой лаборатории мог бы приближать или превышать значение ![]() -статистики Манделя, вычисленной для 95%-го или 99%-го уровня доверия, если критерий Граббса показывает наличие выбросов.
-статистики Манделя, вычисленной для 95%-го или 99%-го уровня доверия, если критерий Граббса показывает наличие выбросов.
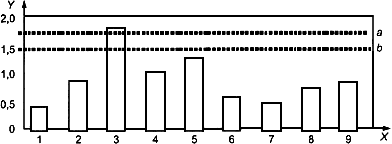
Обозначения:
![]() - номер лаборатории;
- номер лаборатории;
![]() -
- ![]() -статистика Манделя;
-статистика Манделя;
![]() - уровень доверия 99%;
- уровень доверия 99%;
![]() - уровень доверия 95%
- уровень доверия 95%
Рисунок 6 - График ![]() -статистики Манделя
-статистики Манделя
Кроме того, график ![]() -статистики для конкретных исследуемых уровней каждой лаборатории может приближаться или превышать значение
-статистики для конкретных исследуемых уровней каждой лаборатории может приближаться или превышать значение ![]() -статистики Манделя, вычисленной для 95%-го или 99%-го уровня доверия, если критерий Кохрена показывает наличие выбросов.
-статистики Манделя, вычисленной для 95%-го или 99%-го уровня доверия, если критерий Кохрена показывает наличие выбросов.
3.2 Тест на выбросы
3.2.1 Общие точки
3.2.1.1 Уровень доверия
Обработка выбросов описана в ИСО 5725-2 [2], пункты 7.1-7.3. В качестве выброса рассматривают результат, который достаточно сильно отличается от всех других результатов, используемых для дальнейших исследований. В зависимости от типа распределения, которому принадлежат результаты наблюдений, результат, который кажется выбросом, в действительности может им не быть (ИСО 5725-2 [2], пункты 7.3.2.1 и 7.3.3.2, рекомендует уровни доверия 95% для выбросов, которые называют "квазивыбросами", и 99% для выбросов, которые называют "статистическими выбросами"). Для конкретных обстоятельств выбор 95%-ных и 99%-ных уровней доверия означает, что один результат из 20 и один результат из 100, соответственно, могут быть ошибочно истолкованы. Следовательно, этот единственный результат может произойти случайно, а уровень доверия, установленный в ИСО 5725-2 [2], может не соответствовать конкретным требованиям. Он может представлять степень приемлемости, которая недостаточна для некоторых целей. Поэтому предполагается, что в конкретных обстоятельствах необходимо рассматривать вопрос о применении ИСО 5725-2 [2] с используемыми уровнями доверия.
3.2.1.2 Основные предположения
В тестах, используемых для определения наличия или отсутствия выбросов, предполагается, что результаты распределены в соответствии с распределением Гаусса (нормальное распределение, ИСО 5725-2 [2], пункт 1.4) или, по крайней мере, в соответствии с унимодальным распределением (ИСО 5725-2 [2], пункт 7.3.1.7). Следовательно, перед выполнением любого теста, особенно теста, который требует использования большого количества результатов, должна быть сделана проверка этого предположения. Предполагается также (ИСО 5725-2 [2], пункты 1.3 и 5.1.1), что количество результатов в каждом наборе данных (от каждой лаборатории) одинаково и что количество результатов для каждого исследуемого уровня или количество различных образцов является одинаковым. Таким образом, результаты являются "сбалансированными". Если результаты "не сбалансированы", рекомендуется (ИСО 5725-2 [2], пункт 7.2.2) результаты из соответствующих наборов данных отбрасывать случайным образом до достижения "сбалансированной" ситуации. Хотя "сбалансированная" ситуация предпочтительна, признано (даже в пределах примеров, иллюстрированных в ИСО 5725-2 [2]), что "несбалансированные" ситуации могут быть приемлемыми. Далее предполагается (ИСО 5725-1 [1], пункт 4.4, и ИСО 5725-2 [2], пункт 7.3.3.3), что результаты получены в условиях повторяемости. Следовательно, можно предполагать, что образцы для определенного исследуемого уровня являются гомогенными, идентичными во всех отношениях и анализируются в пределах короткого периода времени с использованием одинаковых реактивов и результатов калибровки. Теоретически эти предположения должны быть проведены и удовлетворены до использования любых тестов для проверки наличия или отсутствия выбросов.
3.2.1.3 Декларация о выбросах
При выполнении тестов на выбросы следует понимать, что выбросы не должны отклоняться только по статистическим соображениям. Для каждой выборки причину, по которой результат отличается от всех других, следует исследовать и идентифицировать. Тесты на выбросы, основанные на используемых предположениях, указывают на наличие достаточной статистической причины выбросов, но они не указывают, почему это произошло. Только после проведения полного исследования для идентификации вероятной причины данные могут быть объявлены выбросами и отброшены.
Если конкретный исследуемый уровень проанализирован по критерию Кохрена, Граббса или некоторым другим критериям и никаких выбросов не обнаружено или они идентифицированы, проводят проверку других исследуемых уровней. Если несколько выбросов идентифицировано в различных исследуемых уровнях для данного набора данных, полученных единственной лабораторией, необходимо рассмотреть вопрос о тестировании всех наборов данных для всех исследуемых уровней.
Кроме того, следует решать - надо исключать только выбросы, идентифицированные для этой лаборатории, или надо отклонять весь набор данных этой лаборатории. Необходимые действия определяют индивидуально на основе опыта и знания исследований, выполняемых для идентификации возможных причин.
Контроль выбросов по графикам может получить дополнительное обоснование по результатам тестов на выбросы (количества выбросов). Следовательно, графики ![]() - и
- и ![]() -статистик Манделя допускается использовать для облегчения этих решений. Рассмотрение должно дать отклонение всех результатов лаборатории, если конкретный набор данных (например, для лаборатории 9 на рисунке 5 или для лаборатории 3 на рисунке 6) показывает, что все расчетные значения положительны и близки или превышают приведенные в таблице значения для 95%-ного и 99%-ного уровня доверия. Может быть, что все выборочные средние одной лаборатории больше, чем соответствующие значения всех других лабораторий. Этот факт может быть причиной для беспокойства. Как прежде, решение об отклонении данных следует принимать только на основе соответствующих исследований для выявления вероятной причины выбросов.
-статистик Манделя допускается использовать для облегчения этих решений. Рассмотрение должно дать отклонение всех результатов лаборатории, если конкретный набор данных (например, для лаборатории 9 на рисунке 5 или для лаборатории 3 на рисунке 6) показывает, что все расчетные значения положительны и близки или превышают приведенные в таблице значения для 95%-ного и 99%-ного уровня доверия. Может быть, что все выборочные средние одной лаборатории больше, чем соответствующие значения всех других лабораторий. Этот факт может быть причиной для беспокойства. Как прежде, решение об отклонении данных следует принимать только на основе соответствующих исследований для выявления вероятной причины выбросов.
3.2.1.4 Выбор теста
Для каждой лаборатории или исследуемого уровня, или конкретной выборки большинство тестов на выбросы сравнивает некоторую меру относительного отклонения подозрительного результата от среднего всех результатов и оценивает, возможно ли считать происхождение этого результата случайным. Существует много доступных тестов для практических целей, но не все они полностью описаны в ИСО 5725-2 [2]. Таким образом, в дополнение к тестам, упомянутым в ИСО 5725-2 [2], пункты 7.1-7.3, необходимо понимать, что для определения выбросов допускается использовать другие тесты. Следовательно, необходимость использования тестов на выбросы, описанных в ИСО 5725-2 [2], определяет статистик. Все детали используемого теста должны быть зафиксированы вместе с его результатами.
3.2.2 Критерий Кохрена
3.2.2.1 Основные принципы
Критерий Кохрена используют для проверки, есть ли слишком большие стандартные отклонения базовых элементов в таблице 3, которые увеличивают оценку стандартного отклонения повторяемости, если их сохранять. Статистика, используемая в критерии Кохрена, тесно связана с ![]() -статистикой Манделя.
-статистикой Манделя.
3.2.2.2 Интерпретация
Критерий Кохрена по таблице 3 допускается использовать для определения совместимости небольшой дисперсии для конкретного набора данных с дисперсиями всех наборов данных для исследуемого уровня. Этот критерий определяет отношение наибольшей дисперсии, полученной для конкретной лаборатории, к сумме всех дисперсий, полученных для всех лабораторий. Это подсчитанное значение сравнивают с вычисленным или табличным (критическим) значением отношения и оценивают наличие выбросов.
Критерий Кохрена идентифицирует дисперсии, которые больше средних дисперсий для этого уровня. В этом отношении критерий является односторонним, поскольку лаборатория с наименьшей дисперсией (относительно других лабораторий) не подвергается контролю по этому критерию. Решение о повторении критерия Кохрена зависит от того, идентифицированы ли выбросы, и от количества тестируемых наборов данных на конкретном исследуемом уровне. Если выбросы не обнаружены, то критерий не повторяют. Если выбросы обнаружены, то для проверки повторяют критерий Кохрена на оставшихся наборах данных рассматриваемого уровня. Эта осторожность особенно уместна для небольшого количества данных, особенно если приблизительно 20% данных отклонены как выбросы.
3.2.2.3 Альтернативные критерии
Альтернативой критерию Кохрена являются критерии Бартлетта, Левина и Хартлея. Однако могут быть случаи, когда выбросы идентифицированы с использованием одного критерия, но не идентифицированы при использовании другого критерия. Следовательно, важно чтобы статистик зафиксировал, какие критерии использовались и какие сделаны заключения.
3.2.3 Критерий Граббса
3.2.3.1 Принцип
Критерий Граббса используют для проверки наличия базовых элементов в таблице 2, которые являются слишком большими или слишком маленькими и могут дать большую оценку стандартного отклонения воспроизводимости. Статистика, используемая в критерии Граббса, тесно связана с ![]() -статистикой Манделя.
-статистикой Манделя.
3.2.3.2 Интерпретация
После применения критерия Кохрена сведенные в таблицу средние для каждого конкретного исследуемого уровня, показанного в таблице 2, располагают в неубывающем порядке. Затем выполняют несколько критериев Граббса. Сначала выполняют критерий для определения, являются ли наибольшее или наименьшее среднее единственным выбросом. Если выброс идентифицирован, его отбрасывают и повторяют критерии для следующего подозрительного значения. Для конкретного исследуемого уровня критерий Граббса для одного выброса позволяет вычислять отношение разности подозреваемого значения и среднего всех значений уровня к стандартному отклонению всех значений. Это отношение затем сравнивают с вычисленным или табличным критическим значением отношения с 95%-ным и 99%-ным уровнем доверия.
Если единичный выброс не обнаружен, выполняют критерий Граббса для определения присутствия (или отсутствия) двух выбросов. Например, тестируют два наименьших средних и, если выбросы не обнаружены, тестируют два наибольших средних. В этом критерии, если вычисленное отношение больше расчетного (или табличного) для заданного уровня доверия, среднее расценивают как удовлетворительное.
3.2.3.3 Альтернативные критерии
Альтернативой критерию Граббса является критерий Диксона. Однако возможны ситуации, когда выброс идентифицирован по одному критерию, но не идентифицирован по другому критерию. Следовательно, важно, чтобы статистик фиксировал, какие критерии использовались.
3.3 Заключение
В схеме процесса, приведенной на рисунке 7, указаны основные процедуры, которые должны быть выполнены.

Рисунок 7 - Схема процедуры статистической обработки выбросов
Данные, идентифицированные как статистические выбросы, сообщают ответственному исполнителю. Ответственный исполнитель должен провести необходимые исследования, чтобы принять решение о сохранении, отклонении или изменении этих данных. Когда это исследование завершено, в зависимости от его результата статистик получает пересмотренный набор данных в соответствии с таблицей 1. При необходимости повторно рассчитывают дополнительные таблицы, аналогичные таблицам 2 и 3. Затем статистик оценивает для каждого исследуемого уровня стандартные отклонения повторяемости и воспроизводимости.
4 Оценка стандартных отклонений повторяемости и воспроизводимости
4.1 Дисперсионный анализ
В межлабораторной программе большое количество лабораторий выполняет повторные испытания на одном и том же образце материала. Этот процесс изображен на рисунке 8.

Рисунок 8 - Схема межлабораторной программы
Если образец испытан один раз в различных лабораториях, дисперсия полученных значений характеристики ![]() отразит некоторую комбинацию изменчивости, являющейся результатом внутрилабораторной и межлабораторной изменчивости. Для объяснения генерации отдельных результатов
отразит некоторую комбинацию изменчивости, являющейся результатом внутрилабораторной и межлабораторной изменчивости. Для объяснения генерации отдельных результатов ![]() используется модель, описанная в 4.2.
используется модель, описанная в 4.2.
4.2 Описание модели
Прецизионность (повторяемость и воспроизводимость) метода измерений может быть оценена на основе анализа данных группы лабораторий, отобранных из совокупности лабораторий, использующих один и тот же метод. Каждая лаборатория поставляет набор результатов, который статистически сравнивают с другими наборами результатов.
Примечание - Описанные процедуры допускается также использовать для оценки параметров группы аналитиков или операторов вместо группы лабораторий.
Статистическая обработка основана на следующих предположениях:
- несколько выборок результатов или действий различных уровней анализируются несколькими лабораториями;
- каждая лаборатория выполняет метод испытаний и фиксирует результаты повторений;
- на каждом уровне общее рассеивание результатов формируется за счет случайных изменений.
Этот процесс описан в ИСО 5725-2 [2], пункт 4.1, уравнением:
![]() ,
,
где ![]() - среднее (математическое ожидание) результатов;
- среднее (математическое ожидание) результатов;
![]() - лабораторная составляющая смещения в условиях повторяемости;
- лабораторная составляющая смещения в условиях повторяемости;
![]() - случайное отклонение, имеющее место при любом измерении в условиях повторяемости.
- случайное отклонение, имеющее место при любом измерении в условиях повторяемости.
Наилучшая оценка истинного значения исследуемой характеристики - общее среднее всех результатов ![]() . Единственное фиксируемое значение
. Единственное фиксируемое значение ![]() в общем случае не будет равно
в общем случае не будет равно ![]() .
.
Общая погрешность ![]() содержит две части:
содержит две части: ![]() и
и ![]() (
(![]() - отклонение
- отклонение ![]() от среднего из большого количества результатов, полученных в конкретной лаборатории, в которой значение
от среднего из большого количества результатов, полученных в конкретной лаборатории, в которой значение ![]() было измерено, а
было измерено, а ![]() - отклонение (или разность) между этим концептуальным, средним и общим средним). Это разбиение
- отклонение (или разность) между этим концептуальным, средним и общим средним). Это разбиение ![]() изображено на рисунке 9.
изображено на рисунке 9.

Обозначения:
1 - лаборатория N 1;
2 - лаборатория N 2;
3 - лаборатория N ![]() ;
;
4 - среднее лаборатории N 2;
![]() - дисперсия лабораторной составляющей смещения;
- дисперсия лабораторной составляющей смещения;
![]() - внутрилабораторная дисперсия результатов испытаний
- внутрилабораторная дисперсия результатов испытаний
Рисунок 9 - Разбиение общей погрешности
Ожидается, что ![]() и
и ![]() близки к нулю. Целью ИСО 5725-2 [2] является оценка их дисперсий. Дисперсия
близки к нулю. Целью ИСО 5725-2 [2] является оценка их дисперсий. Дисперсия ![]() - внутрилабораторная дисперсия
- внутрилабораторная дисперсия ![]() , а дисперсия
, а дисперсия ![]() - межлабораторная дисперсия
- межлабораторная дисперсия ![]() .
.
Внутрилабораторная дисперсия - дисперсия повторяемости.
Сумма межлабораторной дисперсии и внутрилабораторной дисперсии ![]() , представляет собой дисперсию результатов, полученных в условиях, которые значительно различаются (например, замена лабораторий), и является дисперсией воспроизводимости
, представляет собой дисперсию результатов, полученных в условиях, которые значительно различаются (например, замена лабораторий), и является дисперсией воспроизводимости ![]() .
.
Структуру, изображенную на рисунке 8, называют вложенной или иерархической схемой. Для оценки дисперсий ![]() и
и ![]() необходимо оценить
необходимо оценить ![]() и
и ![]() .
.
На языке статистики лабораторное воздействие ![]() является случайным. Это означает также, что набор лабораторий, которые участвуют в межлабораторной программе, является случайной выборкой из теоретически бесконечного набора лабораторий, которые могли бы использовать данный метод испытаний. Необходимо оценить, насколько эти лаборатории подобны друг другу.
является случайным. Это означает также, что набор лабораторий, которые участвуют в межлабораторной программе, является случайной выборкой из теоретически бесконечного набора лабораторий, которые могли бы использовать данный метод испытаний. Необходимо оценить, насколько эти лаборатории подобны друг другу.
4.3 Примеры
4.3.1 Пример 1
Поясним, как следует оценивать два компонента дисперсии ![]() и
и ![]() на примере четырех лабораторий, каждая из которых выполняет три повторения измерений одного и того же образца. Потерянные данные и выбросы отсутствуют. Например, зафиксированные данные являются данными, показанными на рисунке 10.
на примере четырех лабораторий, каждая из которых выполняет три повторения измерений одного и того же образца. Потерянные данные и выбросы отсутствуют. Например, зафиксированные данные являются данными, показанными на рисунке 10.

Обозначения:
1 - лаборатория N 1;
2 - лаборатория N 2;
3 - лаборатория N 3;
4 - лаборатория N 4
Рисунок 10 - План эксперимента для примера 1
Оценка ![]() по данным лаборатории
по данным лаборатории ![]() определяется как дисперсия трех результатов:
определяется как дисперсия трех результатов:
![]() . Она имеет две степени свободы.
. Она имеет две степени свободы.
Оценка ![]() по данным лаборатории
по данным лаборатории ![]() определяется как дисперсия трех результатов:
определяется как дисперсия трех результатов:
![]() . Она имеет две степени свободы.
. Она имеет две степени свободы.
Оценка ![]() по данным лаборатории
по данным лаборатории ![]() определяется как дисперсия трех результатов:
определяется как дисперсия трех результатов:
![]() . Она имеет две степени свободы.
. Она имеет две степени свободы.
Оценка ![]() по данным лаборатории
по данным лаборатории ![]() определяется как дисперсия трех результатов:
определяется как дисперсия трех результатов:
![]() . Она имеет две степени свободы.
. Она имеет две степени свободы.
Более хорошую оценку ![]() истинной неизвестной дисперсии повторяемости
истинной неизвестной дисперсии повторяемости ![]() получают усреднением
получают усреднением ![]() ,
, ![]() ,
, ![]() и
и ![]() в соответствии с гипотезой о равенстве четырех дисперсий. Эта гипотеза может быть проверена по критерию Кохрена (см. раздел 2). Для максимальной дисперсии 2,33 и суммы всех дисперсий 5,66 статистика Кохрена равна 2,33/5,66=0,41. Сравнение с критическим значением 0,768 для 5% четырех лабораторий и трех повторений показывает, что равенство дисперсий не может быть отклонено. Следовательно,
в соответствии с гипотезой о равенстве четырех дисперсий. Эта гипотеза может быть проверена по критерию Кохрена (см. раздел 2). Для максимальной дисперсии 2,33 и суммы всех дисперсий 5,66 статистика Кохрена равна 2,33/5,66=0,41. Сравнение с критическим значением 0,768 для 5% четырех лабораторий и трех повторений показывает, что равенство дисперсий не может быть отклонено. Следовательно, ![]() =1,42 и имеет восемь степеней свободы.
=1,42 и имеет восемь степеней свободы.
Имеется четыре выборочных средних (16,00, 14,67, 14,33 и 15,00) по одному для каждой лаборатории. Каждое среднее является оценкой измеряемого параметра. Общее среднее ![]() равно 15,00, а дисперсия равна 0,52 и имеет три степени свободы. Поскольку в этом случае каждое лабораторное среднее является выборочным средним трех отдельных результатов, дисперсия этих средних не является оценкой только
равно 15,00, а дисперсия равна 0,52 и имеет три степени свободы. Поскольку в этом случае каждое лабораторное среднее является выборочным средним трех отдельных результатов, дисперсия этих средних не является оценкой только ![]() , но содержит также часть дисперсии повторяемости (одна треть в этом примере).
, но содержит также часть дисперсии повторяемости (одна треть в этом примере).
Эту информацию представляют в виде таблицы 4.
Таблица 4 - Оценка компонентов дисперсии
|
Оцениваемая величина |
Значение оценки |
|
|
0,52 |
|
|
1,42 |
Приравнивая оценки к соответствующим оцениваемым величинам, можно получать оценки ![]() и
и ![]() для
для ![]() и
и ![]() .
.
Здесь ![]() равна 1,42;
равна 1,42;
![]() равно 0,05 (т.е. 0,52-1,42/3).
равно 0,05 (т.е. 0,52-1,42/3).
Оценка ![]() дисперсии повторяемости определяется как
дисперсии повторяемости определяется как ![]() и равна 1,47 (т.е. 0,05+1,42). Обычно результаты представлены в виде таблицы 5.
и равна 1,47 (т.е. 0,05+1,42). Обычно результаты представлены в виде таблицы 5.
Таблица 5 - Оценка компонентов дисперсии
|
Оцениваемая величина |
Значение оценки |
|
|
1,56 (=3x0,52) |
|
|
1,42 |
Вычисления становятся более сложными, когда количество результатов в лабораториях не равное, и в этом случае рекомендуется использовать соответствующий пакет программ. Однако принцип остается тем же самым.
4.3.2 Пример 2
В таблице 6 приведены необработанные данные, соответствующие средние и дисперсии для различных лабораторий.
Таблица 6 - Пример 1, средние и дисперсии
|
Параметр |
Лаборатория 1 |
Лаборатория 2 |
Лаборатория 3 |
Лаборатория 4 |
|
Результаты |
63 |
44 |
50 |
53 |
|
|
57 |
51 |
40 |
57 |
|
|
54 |
43 |
42 |
46 |
|
Среднее |
58 |
46 |
44 |
52 |
|
|
21 |
19 |
28 |
31 |
|
Число степеней свободы |
2 |
2 |
2 |
2 |
|
Примечание - Индекс | ||||
Из этих результатов, следует:
|
- общее среднее |
50,00, т. е. (58+46+44+52)/4; |
|
- дисперсия средних |
40,00; |
|
- дисперсия повторяемости |
24,75, т. е. (21+19+28+31)/4. |
|
Следовательно, |
|
|
- межлабораторная дисперсия |
31,75, т.е. 40-24,75/3; |
|
- дисперсия воспроизводимости |
56,50, т. е. 31,75+24,75. |
4.4 Использование пределов повторяемости и воспроизводимости
Оценку стандартных отклонений повторяемости и воспроизводимости допускается использовать для определения пределов повторяемости и воспроизводимости. Эти пределы используются на практике для принятия решения о выполнении метода измерений без существенных неблагоприятных воздействий и/или значимых отличиях двух видов продукции.
Пределы повторяемости и воспроизводимости представляют собой абсолютную разность между двумя единственными результатами, полученными в условиях повторяемости и воспроизводимости соответственно, которая не будет превышена в 95% случаев. Грубая оценка пределов повторяемости и воспроизводимости может быть получена перемножением стандартных отклонений повторяемости и воспроизводимости на 2,8 в соответствии с ИСО 5725-6 [6] (пункт 4.1), а также с помощью применения следующих правил:
а) если два результата измерений одной и той же продукции в условиях повторяемости (или условиях воспроизводимости) отличаются больше, чем на предел повторяемости (или воспроизводимости), вероятно, что причина скрыта в неправильном применении метода и/или осуществлении отбора выборки. Рекомендуется дальнейшее исследование. Возможно, будет необходимо большее количество результатов;
b) если два результата измерений двух различных изделий в условиях повторяемости (или условиях воспроизводимости) отличаются больше, чем на предел повторяемости (или воспроизводимости), разумно задать вопрос, имеют ли эти два изделия одинаковое качество.
Примечание - Стандартные отклонения повторяемости и воспроизводимости являются оценками прецизионности, и поэтому их используют для оценки ошибок (погрешностей). Они предназначены для руководства при оценке законности или уместности результатов, полученных методом измерений, а не в качестве жестких числовых критериев для отклонения или утверждения результатов. В частности, значение параметра 2,8, используемых для получения пределов повторяемости и воспроизводимости, основано на предположении о нормальном распределении. Справедливость этого предположения должна быть проверена до измерений, что редко случается на практике. Многие специалисты используют значение три для этого значения параметра без потери информации. Здравый смысл должен преобладать во всех случаях.
Результаты применения этой оценки в примере 2 следующие:
- предел повторяемости ![]() ;
;
- предел воспроизводимости ![]() .
.
Разность двух результатов, полученных для одного изделия в условиях повторяемости (или воспроизводимости), не будет превышать 13,93 (или 21,05) в 95 случаях из 100.
5 Примеры использования статистического программного обеспечения
5.1 Общие положения
Настоящий раздел иллюстрирует, как графики и статистики могут быть получены с использованием статистических программ. Цель - показать главные преимущества автоматизированных расчетов (точность, скорость и возможность использовать процедуры, которые являются слишком усложненными для расчетов на калькуляторе).
Есть некоторые ограничения для использования пакетов программ. Не все пакеты обладают способностью вычислять все необходимые статистические параметры, например ![]() -и
-и ![]() -статистики Манделя или статистику Граббса.
-статистики Манделя или статистику Граббса.
Два примера из ИСО 5725-2 [2] (приложение В) представлены ниже:
- пример 1. ИСО 5725-2 [2], В.1 "Определение содержания серы в угле";
- пример 3. ИСО 5725-2 [2], В.3 "Термометрическое титрование креозотового масла".
По возможности ссылки на пункты этих приложений будут указаны.
5.2 Определение содержания серы в угле
5.2.1 Исходные данные
Данные могут быть введены из таблицы В.1 ИСО 5725-2 [2]. Первая колонка содержит номер лаборатории, а остальные четыре колонки одного уровня содержат данные (см. таблицу 7).
Таблица 7 - Представление данных (содержание серы в угле![]() )
)
|
Лаборатория |
Уровень | |||
|
|
1 |
2 |
3 |
4 |
|
1 |
0,71 |
1,20 |
1,68 |
3,26 |
|
1 |
0,71 |
1,18 |
1,70 |
3,26 |
|
1 |
0,70 |
1,23 |
1,68 |
3,20 |
|
1 |
0,71 |
1,21 |
1,69 |
3,24 |
|
2 |
0,69 |
1,22 |
1,64 |
3,20 |
|
2 |
0,67 |
1,21 |
1,64 |
3,20 |
|
2 |
0,68 |
1,22 |
1,65 |
3,20 |
|
3 |
0,66 |
1,28 |
1,61 |
3,37 |
|
3 |
0,65 |
1,31 |
1,61 |
3,36 |
|
3 |
0,69 |
1,30 |
1,62 |
3,38 |
|
4 |
0,67 |
1,23 |
1,68 |
3,16 |
|
4 |
0,65 |
1,18 |
1,66 |
3,22 |
|
4 |
0,66 |
1,20 |
1,66 |
3,23 |
|
5 |
0,70 |
1,31 |
1,64 |
3,20 |
|
5 |
0,69 |
1,22 |
1,67 |
3,19 |
|
5 |
0,66 |
1,22 |
1,60 |
3,18 |
|
5 |
0,71 |
1,24 |
1,66 |
3,27 |
|
5 |
0,69 |
- |
1,68 |
3,24 |
|
6 |
0,73 |
1,39 |
1,70 |
3,27 |
|
6 |
0,74 |
1,36 |
1,73 |
3,31 |
|
6 |
0,73 |
1,37 |
1,73 |
3,29 |
|
7 |
0,71 |
1,20 |
1,69 |
3,27 |
|
7 |
0,71 |
1,26 |
1,70 |
3,24 |
|
7 |
0,69 |
1,26 |
1,68 |
3,23 |
|
8 |
0,70 |
1,24 |
1,67 |
3,25 |
|
8 |
0,65 |
1,22 |
1,68 |
3,26 |
|
8 |
0,68 |
1,30 |
1,67 |
3,26 |
|
| ||||
Альтернативно данные могут быть также введены из трех колонок одной лаборатории по одному из каждого уровня. В этом случае содержание серы выражается в процентах массы. Пример такого расположения данных приведен в таблице 8 для лабораторий 1 и 2. Весь файл в этом случае включает также данные лабораторий 3-8.
Таблица 8 - Альтернативное представление данных (содержание серы в угле![]() ) лабораторий 1 и 2
) лабораторий 1 и 2
|
Лаборатория |
Уровень |
Содержание серы |
|
1 |
1 |
0,71 |
|
1 |
1 |
0,71 |
|
1 |
1 |
0,70 |
|
1 |
1 |
0,71 |
|
1 |
2 |
1,20 |
|
1 |
2 |
1,18 |
|
1 |
2 |
1,23 |
|
1 |
2 |
1,21 |
|
1 |
3 |
1,68 |
|
1 |
3 |
1,70 |
|
1 |
3 |
1,68 |
|
1 |
3 |
1,69 |
|
1 |
4 |
3,26 |
|
1 |
4 |
3,26 |
|
1 |
4 |
3,20 |
|
1 |
4 |
3,24 |
|
2 |
1 |
0,69 |
|
2 |
1 |
0,67 |
|
2 |
1 |
0,68 |
|
2 |
2 |
1,22 |
|
2 |
2 |
1,21 |
|
2 |
2 |
1,22 |
|
2 |
3 |
1,64 |
|
2 |
3 |
1,64 |
|
2 |
3 |
1,65 |
|
2 |
4 |
3,20 |
|
2 |
4 |
3,20 |
|
2 |
4 |
3,20 |
|
| ||
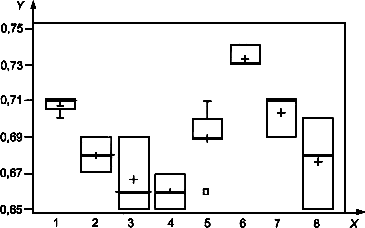
Как уже было отмечено, для выявления потенциальных выбросов рекомендуется данные изображать графически. Ниже приведены два примера таких графических представлений. Разброс необработанных данных уровня 1 показан на рисунке 11, аналогичном рисункам В.1-В.4 по ИСО 5725-2 [2]. Эти графики показывают расположение результатов лабораторий вдоль горизонтальной линии, соответствующей значению общего среднего. График "квадратики и усики", представленный на рисунке 12, состоит из квадратиков и выбросов, включающих все результаты лабораторий уровня 1, и полезен при проведении начальной оценки потенциальных выбросов. Это очень информативный способ исследования данных.
Выборочное среднее и медиана для каждой лаборатории изображены соответственно крестиком и более жирной линией. Основание квадратика является первой квартилью (![]() ), а вершина - третьей квартилью (
), а вершина - третьей квартилью (![]() ). Приближенный диапазон изменения данных изображен линиями, называемыми усиками, которые идут от вершины и основания квадратика до наибольшего и наименьшего значений данных соответственно. Эти значения все еще находятся в области, ограниченной следующими пределами:
). Приближенный диапазон изменения данных изображен линиями, называемыми усиками, которые идут от вершины и основания квадратика до наибольшего и наименьшего значений данных соответственно. Эти значения все еще находятся в области, ограниченной следующими пределами:
- нижний предел=![]() ;
;
- верхний предел=![]() .
.
Для нормального распределения (распределение Гаусса) это соответствует интервалу, включающему приблизительно 99,30% значений случайной величины. Джон Такей изобретатель графика "квадратики и усики" назвал эти пределы "внутренними барьерами". Далее он определил "внешние барьеры", полученные с использованием множителя 3 вместо 1,5. Точки данных между "внутренними" и "внешними" барьерами определяют как возможные выбросы. Данные, лежащие вне "внешнего" барьера, являются очень подозрительными, поскольку внутренняя область внешних барьеров охватывает 99,99% интервала значений переменной. Некоторые статистические пакеты программ используют различные символы для этих двух типов выбросов, например "*" для данных, попадающих между внутренними и внешними барьерами, и "0" для данных, лежащих вне внешних барьеров.
Оба графика показывают, что все результаты для лаборатории 6 находятся выше, чем соответствующие значения для других лабораторий. Кроме того, имеются значения для лаборатории 5, легко идентифицируемые на рисунке 12, которые требуют дальнейших исследований.
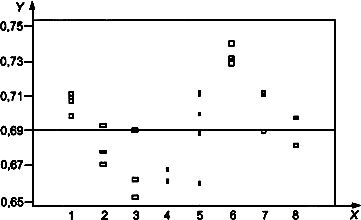
Обозначения:
![]() - номер лаборатории;
- номер лаборатории;
![]() - концентрация, процент массы;
- концентрация, процент массы;
![]() - общее среднее
- общее среднее ![]() , равное 0,69
, равное 0,69
Рисунок 11 - График разброса данных уровня 1
Обозначения:
![]() - номер лаборатории;
- номер лаборатории;
![]() - концентрация, процент массы;
- концентрация, процент массы;
![]() - медиана;
- медиана;
![]() - выборочное среднее;
- выборочное среднее;
![]() - усик
- усик
Рисунок 12 - График "квадратики и усики" данных уровня 1
5.2.2 Таблица средних и стандартных отклонений базового элемента
В таблице 9 показаны результаты расчетов, рассматриваемые в ИСО 5725-2 [2], пункты В.1.3 и В.1.4, для межлабораторных испытаний с помощью типичного пакета программ.
Значения в соответствии с ИСО 5725-2 [2] (таблицы 2 и 3) необходимы для расчета статистик Манделя ![]() и
и ![]() , а также статистик критерия Граббса, которые, как правило, не вычисляются во многих пакетах программ.
, а также статистик критерия Граббса, которые, как правило, не вычисляются во многих пакетах программ.
Таблица 9 - Таблица средних и стандартных отклонений базового элемента
|
Номер лаборатории |
Количество данных |
Среднее |
Стандартное отклонение |
|
Общее | |||
|
- |
27 |
0,69037 |
0,02549 |
|
для отдельных лабораторий | |||
|
1 |
4 |
0,70750 |
0,00500 |
|
2 |
3 |
0,68000 |
0,01000 |
|
3 |
3 |
0,66667 |
0,02082 |
|
4 |
3 |
0,66000 |
0,01000 |
|
5 |
5 |
0,69000 |
0,01871 |
|
6 |
3 |
0,73333 |
0,00577 |
|
7 |
3 |
0,70333 |
0,01155 |
|
8 |
3 |
0,67667 |
0,02517 |
5.2.3 Исследование непротиворечивости данных и выбросов
Во многих пакетах программ применяют несколько критериев однородности, включая критерии Кохрена, Бартлетта, Хартлея и Левина. Результаты этих тестов для данных по содержанию серы в угле приведены в таблице 10.
Таблица 10 - Исследование непротиворечивости и выбросов
|
Тест |
Статистика |
|
|
|
0,350 |
0,308 |
|
Бартлетта |
1,679 |
0,296 |
|
Левина |
1,679 |
0,332 |
|
Хартлея |
25,333 |
- |
![]() -значение представляет собой вероятность наблюдения данного значения статистики, если дисперсии гомогенны. Низкое
-значение представляет собой вероятность наблюдения данного значения статистики, если дисперсии гомогенны. Низкое ![]() -значение (0,05 или ниже) является достаточным для вывода, что внутрилабораторные дисперсии различны. Следовательно, для критерия Кохрена недостаточно оснований для вывода, что внутрилабораторные дисперсии различны.
-значение (0,05 или ниже) является достаточным для вывода, что внутрилабораторные дисперсии различны. Следовательно, для критерия Кохрена недостаточно оснований для вывода, что внутрилабораторные дисперсии различны.
5.2.4 Вычисление общего среднего и стандартных отклонений повторяемости и воспроизводимости
В соответствии с ИСО 5725-2 [2] и ИСО 5725-3 [3] для вычисления ![]() и
и ![]() (стандартных отклонений повторяемости и воспроизводимости для уровня
(стандартных отклонений повторяемости и воспроизводимости для уровня ![]() ) допускается использовать методы регрессионного анализа.
) допускается использовать методы регрессионного анализа.
Большинство пакетов программ позволяет вычислять компоненты дисперсии. Эти возможности дают и другие статистические программы, в том числе предназначенные для "Компонент дисперсии" или "Иерархических планов", или "Вложенных планов".
Вложение заключается в том, что проанализированные образцы отличаются от лаборатории к лаборатории, даже если они взяты из одной единственной партии продукции. Поэтому образцы являются вложенными по отношению к "лабораториям" или, наоборот, лаборатории расположены иерархически выше образцов.
Если такого выбора не существует, необходимо использовать "однофакторный" дисперсионный анализ, где фактор "лаборатория" ("единственный" фактор) является случайным.
Компоненты дисперсии соответствуют разделению полной дисперсии на две части: внутрилабораторную дисперсию ![]() и межлабораторную дисперсию
и межлабораторную дисперсию ![]() соответственно. Пример результатов однофакторного дисперсионного анализа приведен в таблице 11 для уровня 1 (
соответственно. Пример результатов однофакторного дисперсионного анализа приведен в таблице 11 для уровня 1 (![]() =1).
=1).
Таблица 11 - Анализ компонентов дисперсии. Дисперсионный анализ для содержания серы. Уровень 1
|
Источник |
Сумма |
Степень |
Средний квадрат |
Компонент дисперсии |
Процент |
|
Лаборатория |
0,0125546 |
7 |
0,0017935 |
0,0004665 |
67,1 |
|
Ошибка |
0,0043417 |
19 |
0,0002285 |
0,0002285 |
32,8 |
|
Общие данные (скорректированные) |
0,0168963 |
26 |
- |
- |
- |
Стандартное отклонение повторяемости ![]() является квадратным корнем компонента дисперсии "ошибки". Следовательно:
является квадратным корнем компонента дисперсии "ошибки". Следовательно:
![]() .
.
Стандартное отклонение воспроизводимости ![]() является квадратным корнем суммы компонента дисперсии "ошибки" и компонента дисперсии "лаборатории". Следовательно:
является квадратным корнем суммы компонента дисперсии "ошибки" и компонента дисперсии "лаборатории". Следовательно:
![]() .
.
Относительный вес компонента дисперсии "лаборатории" и компонента дисперсии "ошибки" для дисперсии воспроизводимости указан в графе "Процент".
Если этот выбор недоступен, то таблица дисперсионного анализа не может показать компоненты дисперсии непосредственно, и результаты могут быть показаны в виде, представленном в таблице 12. Все эти величины могут быть получены с помощью ручных вычислений при использовании формулы, приведенной в ИСО 5725-2 [2], пункт 7.4.5.2.
Таблица 12 - Таблица результатов дисперсионного анализа для содержания серы. Уровень 1.
|
Источник данных |
Сумма квадратов |
Степень свободы |
Средний квадрат отклонений |
|
|
|
Разные лаборатории |
0,0125546 |
7 |
0,0017935 |
7,85 |
0,0002 |
|
В пределах лаборатории (ошибка) |
0,0043417 |
19 |
0,0002285 |
- |
- |
|
Общие данные (скорректированные) |
0,0168963 |
26 |
- |
- |
- |
Параметр ![]() равен значению внутрилабораторного среднего квадрата отклонений (
равен значению внутрилабораторного среднего квадрата отклонений (![]() =0,0002285) в соответствии с ИСО 5725-2 [2], 7.4.5.2, уравнение (21).
=0,0002285) в соответствии с ИСО 5725-2 [2], 7.4.5.2, уравнение (21).
![]() ,
,
где ![]() - лабораторный средний квадрат отклонений (
- лабораторный средний квадрат отклонений (![]() =0,00179352);
=0,00179352);
![]() =0,0002285 (см. выше);
=0,0002285 (см. выше);
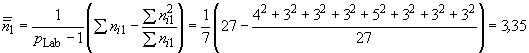 .
.
Примечание - Приближением ![]() является среднее количество результатов на лабораторию (то есть 27/8=3,375).
является среднее количество результатов на лабораторию (то есть 27/8=3,375).
Следовательно:
![]() .
.
Так как ![]() , то
, то ![]() .
.
5.2.5 Зависимость прецизионности от ![]()
После повторения статистического анализа для всех других уровней аналогично определяют стандартные отклонения повторяемости и воспроизводимости.
Данные могут быть представлены аналогично таблице 13.
Таблица 13 - Стандартные отклонения повторяемости и воспроизводимости для нескольких уровней
|
Уровень |
Общее среднее |
Стандартное отклонение повторяемости |
Стандартное отклонение воспроизводимости |
|
1 |
0,690 |
0,015 |
0,026 |
|
2 |
1,252 |
0,029 |
0,061 |
|
3 |
1,667 |
0,017 |
0,035 |
|
4 |
3,250 |
0,026 |
0,058 |
Зависимость прецизионности от общего среднего уровня (см. также ИСО 5725-2 [2], пункт В.1.7) может быть оценена на основе исследования графика рассеивания, приведенного ниже. Средние стандартных отклонений повторяемости и воспроизводимости (0,022 и 0,045 соответственно) могут быть изображены, как показано на рисунке 13.

Обозначения:
![]() - общее среднее в процентах массы;
- общее среднее в процентах массы;
![]() - процент массы;
- процент массы;
![]() - повторяемость;
- повторяемость;
![]() - воспроизводимость;
- воспроизводимость;
![]() - среднее
- среднее ![]() ;
;
![]() - среднее
- среднее ![]()
Рисунок 13 - График ![]() ,
, ![]() от общего среднего
от общего среднего
5.3 Термометрическое титрование креозотового масла
5.3.1 Исходные данные
Графическое изображение необработанных исходных данных (ИСО 5725-2 [2], пункт В.3.2) для термометрического титрования креозотового масла показывает, что данные лаборатории 1 всегда лежат выше, чем данные других лабораторий. Этот факт требует дальнейшего исследования. Проверке на выбросы должна установить, можно ли эти данные включать в рассмотрение.
а) Проверка дисперсии уровня 1
|
|
|
|
Критерий Бартлетта: 3,83936; |
|
|
Критерий Хартлея: 784,0; |
|
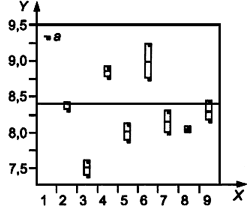
b) Проверка дисперсии уровня 2
|
|
|
|
Критерий Бартлетта: 2,27414; |
|
|
Критерий Хартлея: 256,0; |
|

с) Проверка дисперсии уровня 3
|
|
|
|
Критерий Бартлетта: 2,1715; |
|
|
Критерий Хартлея: 39,0625; |
|
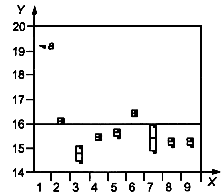
d) Проверка дисперсии уровня 4
|
|
|
|
Критерий Бартлетта: 3,27136; |
|
|
Критерий Хартлея: 121,0; |
|
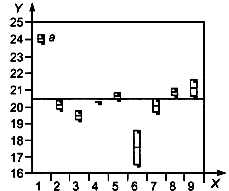
е) Проверка дисперсии уровня 5
|
|
|
|
Критерий Бартлетта: 2,48546; |
|
|
Критерий Хартлея: 50,0051; |
|
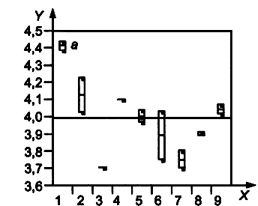
Обозначения:
![]() - номер лаборатории;
- номер лаборатории;
![]() - процент массы креозота;
- процент массы креозота;
![]() - среднее всех средних для лабораторий;
- среднее всех средних для лабораторий;
![]() - систематически более высокое значение
- систематически более высокое значение
Рисунок 14 - Графики "квадратики и усики" и критерии для дисперсии
График "квадратики и усики" четко показывает, что лаборатория 1 систематически дает более высокие значения, чем другие лаборатории, а лаборатории 6 и 7 дают более высокую изменчивость на некоторых уровнях.
5.3.2 Исследование согласованности данных и выбросов
Для оценки согласованности данных и идентификации выбросов данные могут быть представлены в виде таблицы 14 (см. также ИСО 5725-2 [2], пункты В.3.2 и В.3.5).
ПРИМЕР
Для уровня 3 и лаборатории 1 единственное высокое значение статистики Граббса
![]() .
.
Критические значения для 5%-ного и 1%-ного уровней значимости - 2,215 и 2,387 соответственно для этих девяти лабораторий. Следовательно, с 99%-ной уверенностью данные для уровня 3 и лаборатории 1 можно рассматривать как выбросы.
Таблица 14 - Исследование согласованности и выбросов для лаборатории и уровня
|
Лаборатория |
Наблюдение |
Среднее | ||||
|
|
|
Уровня 1 |
Уровня 2 |
Уровня 3 |
Уровня 4 |
Уровня 5 |
|
1 |
Высокое |
4,415 |
9,340 |
|
19,230 |
24,140 |
|
2 |
- |
4,130 |
8,375 |
14,460 |
16,140 |
20,155 |
|
3 |
- |
3,700 |
7,590 |
13,600 |
14,800 |
19,500 |
|
4 |
- |
4,100 |
8,865 |
14,400 |
15,550 |
20,300 |
|
5 |
- |
4,005 |
8,005 |
13,825 |
15,660 |
20,700 |
|
6 |
- |
3,890 |
9,000 |
13,980 |
16,500 |
17,570 |
|
7 |
- |
3,750 |
8,150 |
14,150 |
15,450 |
20,100 |
|
8 |
- |
3,905 |
8,055 |
14,840 |
15,315 |
20,940 |
|
9 |
- |
4,045 |
8,305 |
14,170 |
15,290 |
21,185 |
|
Параметр |
Значение параметра | |||||
|
Среднее |
3,993 |
8,399 |
|
15,993 |
20,511 | |
|
Стандартное отклонение |
0,216 |
0,572 |
1,056 |
1,310 |
1,727 | |
|
Среднее стандартной ошибки |
0,072 |
0,191 |
0,352 |
0,437 |
0,576 | |
5.3.3 Вычисление общих средних стандартных отклонений повторяемости и воспроизводимости
На основании вышеизложенного все данные лаборатории 1 и данные уровня 5 лаборатории 6 отклонены. После этого проводят анализ дисперсии для уровня 5 (![]() =5) и вычисляют стандартные отклонения повторяемости и воспроизводимости
=5) и вычисляют стандартные отклонения повторяемости и воспроизводимости ![]() и
и ![]() соответственно, как показано в таблице 15 (см. также ИСО 5725-2 [2], пункт В.3.6).
соответственно, как показано в таблице 15 (см. также ИСО 5725-2 [2], пункт В.3.6).
Таблица 15 - Анализ дисперсий уровня 5 для данных термометрического титрования креозота
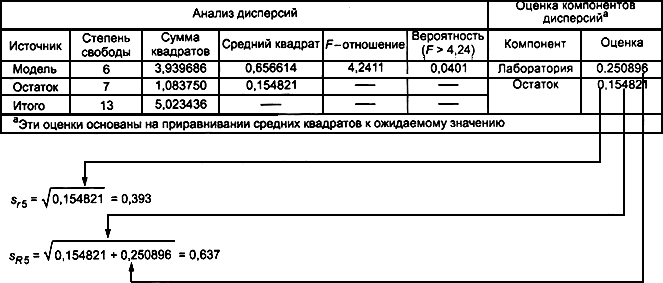
Средний квадрат модели равен оценке величины ![]() .
.
Средний квадрат остатка равен оценке ![]() .
.
5.3.4 Зависимость прецизионности от ![]()
После отклонения выбросов заново подсчитывают общие средние и соответствующие стандартные отклонения повторяемости и воспроизводимости, как показано в таблице 16 (см. также ИСО 5725-2 [2], пункт В.3.7).
Таблица 16 - Прецизионность как функция общих средних для данных термометрического титрования креозота
|
Уровень |
Общее среднее |
Стандартное отклонение повторяемости |
Стандартное отклонение воспроизводимости |
|
1 |
3,94 |
0,092 |
0,171 |
|
2 |
8,28 |
0,179 |
0,498 |
|
3 |
14,18 |
0,127 |
0,400 |
|
4 |
15,59 |
0,337 |
0,579 |
|
5 |
20,41 |
0,393 |
0,637 |
Зависимость прецизионности от общего среднего уровня может быть оценена на основе исследования графика разброса данных, представленного на рисунке 15.
В этом случае линейный регрессионный анализ является более подходящим (угол наклона значимо отличается от 0), чем анализ средних стандартных отклонений повторяемости и воспроизводимости (см. рисунок 15).
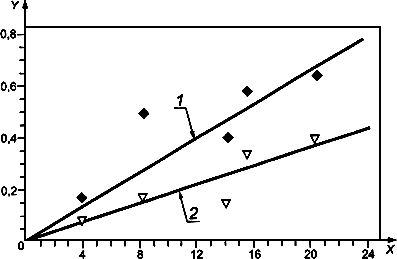
Обозначения:
![]() - общее среднее
- общее среднее ![]() , выраженное в долях массы;
, выраженное в долях массы;
![]() - стандартное отклонение, выраженное в долях массы;
- стандартное отклонение, выраженное в долях массы;
1 - стандартное отклонение воспроизводимости ![]() ;
;
2 - стандартное отклонение повторяемости ![]()
Рисунок 15 - Графики ![]() и
и ![]() для данных термометрического титрования креозота
для данных термометрического титрования креозота
В таблицах 17 и 18 представлены результаты регрессионного анализа стандартного отклонения повторяемости и воспроизводимости соответственно. Хотя это не имеет смысла с физико-химической точки зрения, для наглядности прямая линия была проведена через начало координат, как показано на рисунке 15. Сложность состоит в том, что значения среднего и прецизионности являются оценками и, таким образом, включают ошибки. Для получения хорошей оценки параметров линии регрессии необходимо применять регрессионный анализ с весовыми коэффициентами, который обычно не выполняется, поскольку в большинстве случаев угол наклона прямой является небольшим.
Таблица 17 - Стандартное отклонение повторяемости для данных термометрического титрования креозота
|
Регрессионный анализ | |||||||||
|
Параметр |
Оценка |
Стандартная ошибка |
|
Вероятность | |||||
|
среднее уровня |
0,0179096 |
0,0023917 |
7,48862 |
0,0023917 | |||||
|
Дисперсионный анализ | |||||||||
|
Источник |
Сумма квадратов |
Число степеней свободы |
Средний квадрат |
|
Вероятность ( | ||||
|
Модель |
0,303037 |
1 |
0,303037 |
56,08 |
0,0017 | ||||
|
Остаток |
0,021615 |
4 |
0,005404 |
- |
- | ||||
|
Итого |
0,324652 |
5 |
- |
- |
- | ||||
|
Квадратный корень среднего квадрата остатка равен 0,073510. | |||||||||
|
| |||||||||
Таблица 18 - Стандартное отклонение воспроизводимости для данных термометрического титрования креозота
|
Регрессионный анализ | ||||||||
|
Параметр |
Оценка |
Стандартная ошибка |
|
Вероятность | ||||
|
среднее уровня |
0,0343967 |
0,0040001 |
8,599 |
0,0010 | ||||
|
Дисперсионный анализ | ||||||||
|
Источник |
Сумма квадратов |
Число степеней свободы |
Средний квадрат |
|
Вероятность ( | |||
|
Модель |
1,117790 |
1 |
1,117790 |
73,94 |
0,0010 | |||
|
Остаток |
0,060468 |
4 |
0,015117 |
- |
- | |||
|
Итого |
1,178258 |
5 |
- |
- |
- | |||
|
Квадратный корень среднего квадрата остатка равен 0,122951. | ||||||||
|
| ||||||||
Так как ![]() -значения меньше 0,05, зависимость прецизионности от общего среднего для конкретного уровня может быть представлена выражениями:
-значения меньше 0,05, зависимость прецизионности от общего среднего для конкретного уровня может быть представлена выражениями:
![]() ;
;![]() .
.
Эти выражения допускается использовать для оценки стандартного отклонения повторяемости и воспроизводимости на промежуточных уровнях в пределах диапазона исследуемых уровней.
Например, если требуются стандартные отклонения повторяемости и воспроизводимости для среднего ![]() (
(![]() =12), тогда
=12), тогда
![]() .
.
Приложение А
(обязательное)
Обозначения и сокращения
Все используемые обозначения и сокращения соответствуют обозначениям и сокращениям ИСО 5725-1 - ИСО 5725-6 [1-6], за исключением того, что символ ![]() заменен на
заменен на ![]() , чтобы более четко отличать его от символа
, чтобы более четко отличать его от символа ![]() , используемого для "вероятности".
, используемого для "вероятности".
|
|
- Отрезок, отсекаемый на оси ординат функцией |
|
|
- Показатель, используемый для расчета неопределенности оценки; |
|
|
- Угловой коэффициент функции |
|
|
- Лабораторная составляющая отклонения от общего среднего (лабораторная составляющая смещения); |
|
|
- Составляющая величины |
|
|
- Составляющая величины |
|
|
- Отрезок, отсекаемый на оси ординат функцией ( |
|
|
- Угловой коэффициент прямой ( |
|
|
- Составляющая результата измерений, представляющая случайную погрешность каждого результата измерений; |
|
|
- |
|
|
- Статистика Граббса; |
|
|
- Статистика Манделя для межлабораторной совместимости; |
|
|
- Статистика Манделя для внутрилабораторной совместимости; |
|
|
- Общее среднее значение измеряемой характеристики; уровень; |
|
|
- Количество факторов, рассматриваемых в условиях промежуточной прецизионности; |
|
|
- Количество повторений (итераций); |
|
|
- Количество результатов измерений, полученных в одной лаборатории на одном уровне (то есть в пределах базового элемента); |
|
|
- Количество лабораторий, участвующих в межлабораторном эксперименте; |
|
|
- Вероятность, |
|
|
- Количество уровней измеряемой характеристики в межлабораторном эксперименте; |
|
|
- Предел повторяемости (сходимости); |
|
|
- Предел воспроизводимости; |
|
|
- Оценка стандартного отклонения; |
|
|
- Количество объектов испытаний или групп объектов; |
|
|
- Заданное значение, используемое для критерия Граббса; |
|
|
- Результат измерений (испытаний); |
|
|
- Среднее арифметическое значение результатов измерений (испытаний); |
|
|
- Смещение (систематическая погрешность) метода измерений; |
|
|
- Оценка |
|
|
- Истинное или принятое опорное значение измеряемой величины (характеристики); |
|
|
- Число степеней свободы; |
|
|
- Истинное значение стандартного отклонения. |
|
|
Символы, используемые в качестве подстрочных индексов: |
|
|
- Идентификатор уровня (ИСО 5725-2 [2]); |
|
|
Идентификатор группы испытаний или для фактора (ИСО 5725-3 [3]); |
|
|
- Межлабораторный идентификатор; |
|
|
- Различие, обусловленное неидентичностью элементов выборки проб (образцов); |
|
|
- Различие, определяемое сменой оператора; |
|
|
- Вероятность; |
|
|
- Повторяемость; |
|
|
- Воспроизводимость; |
|
1, 2, 3, ... |
- Для результатов измерений, нумеруемых в порядке их получения; |
|
(1), (2), (3), ... |
Для результатов измерений (испытаний), нумеруемых в порядке возрастания измеряемой величины. |
Приложение В
(справочное)
Сведения о соответствии международных стандартов ссылочным
национальным стандартам Российской Федерации
Таблица В.1
|
Обозначение ссылочного международного стандарта |
Обозначение и наименование соответствующего национального стандарта |
|
ИСО 5725-1:1994 |
|
|
ИСО 5725-2:1994 |
ГОСТ Р ИСО 5725-2:2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения измерения повторяемости и воспроизводимости стандартного метода измерений |
|
ИСО 5725-3:1994 |
ГОСТ Р ИСО 5725-3:2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений |
|
ИСО 5725-4:1994 |
ГОСТ Р ИСО 5725-4:2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений |
|
ИСО 5725-5:1994 |
ГОСТ Р ИСО 5725-5:2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений |
|
ИСО 5725-6:1994 |
ГОСТ Р ИСО 5725-6:2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике |
Библиография
|
[1] ИСО 5725-1:1994 |
Точность (правильность и прецизионность) методов и результатов измерений - Часть 1: Основные положения и определения |
|
[2] ИСО 5725-2:1994 |
Точность (правильность и прецизионность) методов и результатов измерений - Часть 2: Основной метод определения измерения повторяемости и воспроизводимости стандартного метода измерений |
|
[3] ИСО 5725-3:1994 |
Точность (правильность и прецизионность) методов и результатов измерений - Часть 3: Промежуточные показатели прецизионности стандартного метода измерений |
|
[4] ИСО 5725-4:1994 |
Точность (правильность и прецизионность) методов и результатов измерений - Часть 4: Основные методы определения правильности стандартного метода измерений |
|
[5] ИСО 5725-5:1994 |
Точность (правильность и прецизионность) методов и результатов измерений - Часть 5: Альтернативные методы определения прецизионности стандартного метода измерений |
|
[6] ИСО 5725-6:1994 |
Точность (правильность и прецизионность) методов и результатов измерений - Часть 6: Использование значений точности на практике |

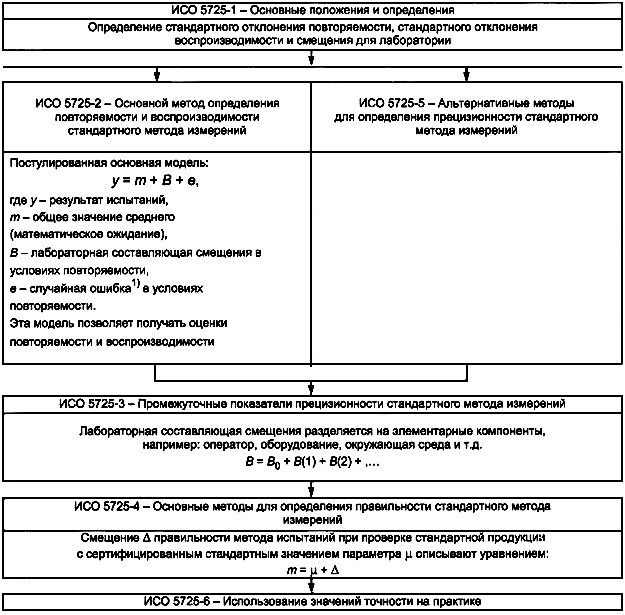
 «Я сейчас офигел!» Врач Алексея Чумакова шокировала певца на...
«Я сейчас офигел!» Врач Алексея Чумакова шокировала певца на...  Создайте свой интернет-магазин на новой платформе ReadyScript
Создайте свой интернет-магазин на новой платформе ReadyScript  Хостинг, домены, VPS/VDS, размещение серверов
Хостинг, домены, VPS/VDS, размещение серверов