ГОСТ Р 50779.74-99 (ИСО 3951-89) Статистические методы. Процедуры выборочного контроля и карты контроля по количественному признаку для процента несоответствующих единиц продукции (Главы I-IV)
ГОСТ Р 50779.74-99 (ИСО 3951-89) Статистические методы. Процедуры выборочного контроля и карты контроля по количественному признаку для процента несоответствующих единиц продукции (Глава IV, Приложения А-Е)

Диаграмма s-L - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки L (объем выборки - 75)
          

Диаграмма s-М - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки М (объем выборки - 100)
          

Диаграмма s-N - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки N (объем выборки - 150)
          

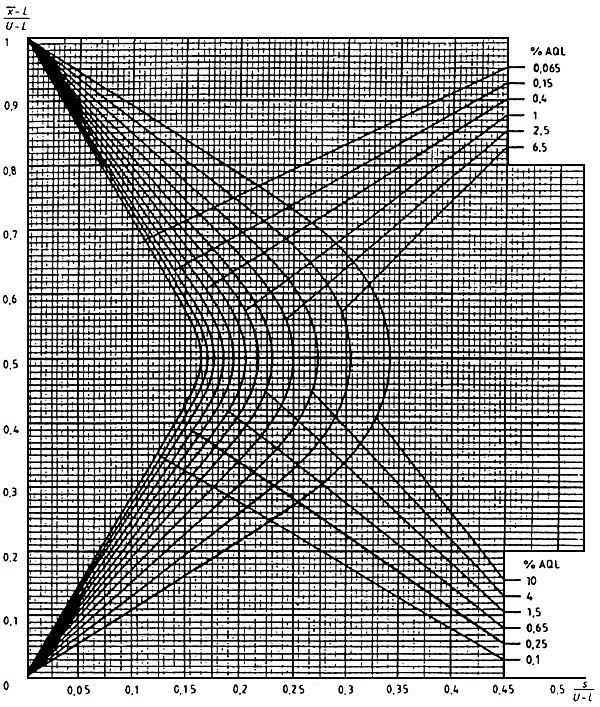
Диаграмма s-Р - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки Р (объем выборки - 200)
          

Диаграмма -С - Кривые приемки для предельных значений с общим уровнем качества: - метод для кода объема выборки С
     

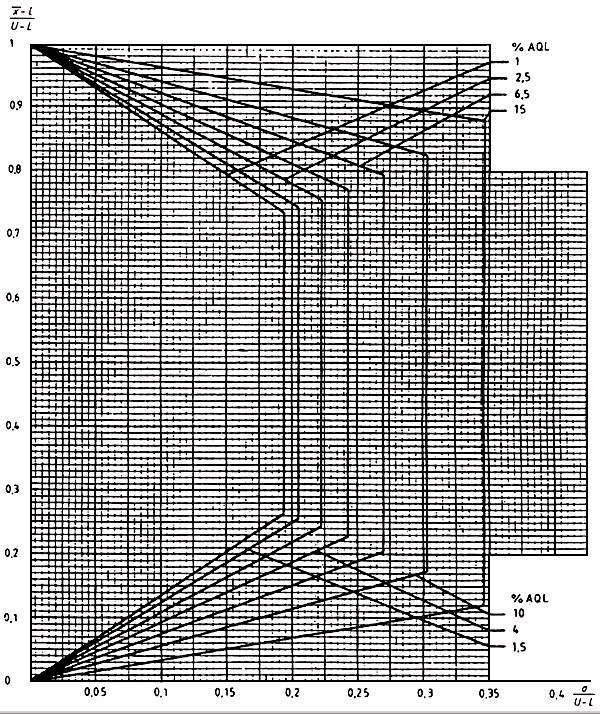
Диаграмма -D - Кривые приемки для предельных значений с общим уровнем качества: - метод для кода объема выборки D
          

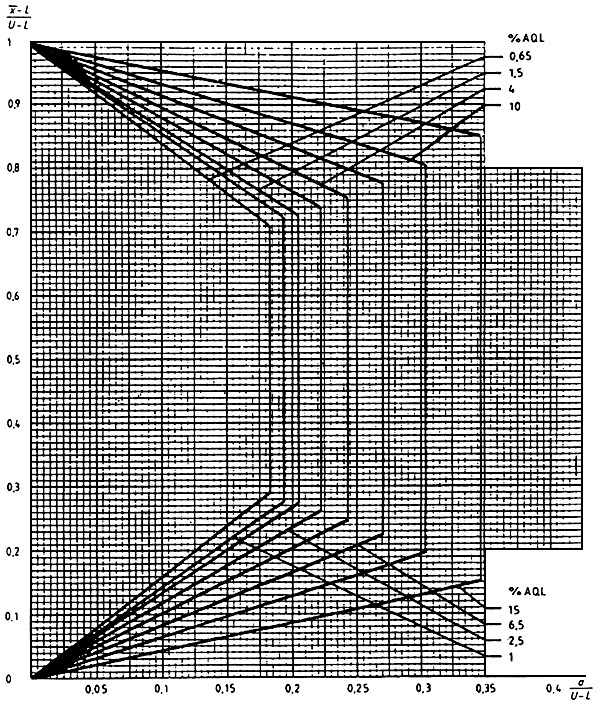
Диаграмма -Е - Кривые приемки для предельных значений с общим уровнем качества: - метод для кода объема выборки Е
          

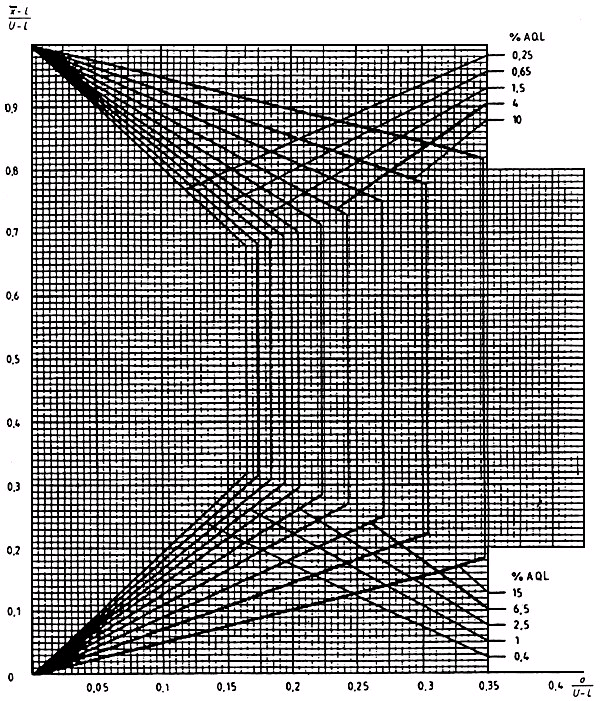
Диаграмма -F - Кривые приемки для предельных значений с общим уровнем качества: - метод для кода объема выборки F
          

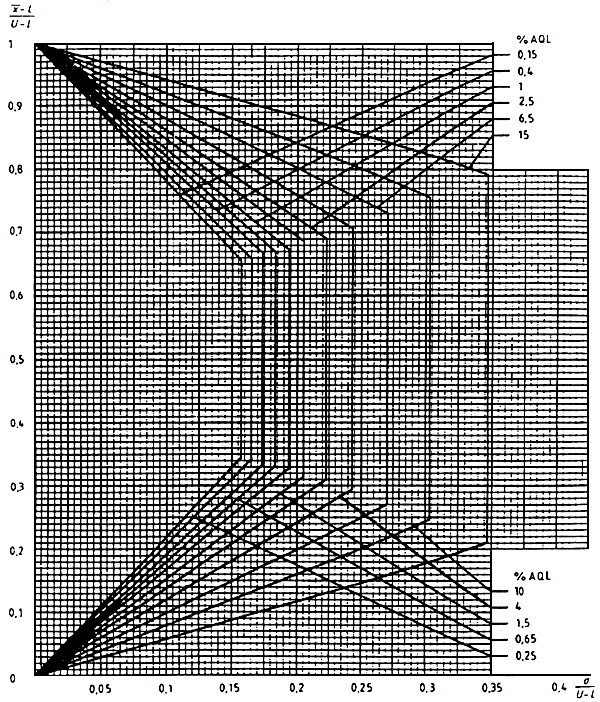
Диаграмма -G - Кривые приемки для предельных значений с общим уровнем качества: - метод для кода объема выборки G
          

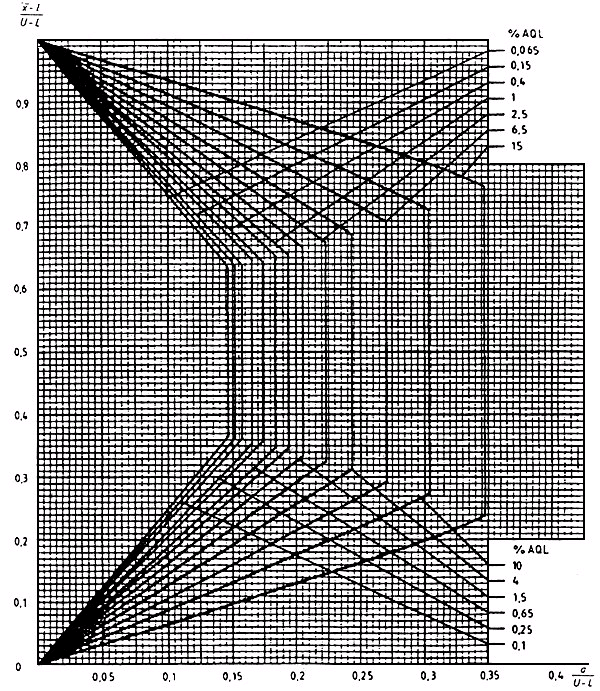
Диаграмма -Н - Кривые приемки для предельных значений с общим уровнем качества: - метод для кода объема выборки Н
          

Диаграмма -I - Кривые приемки для предельных значений с общим уровнем качества: - метод для кода объема выборки I
          

Диаграмма -J - Кривые приемки для предельных значений с общим уровнем качества: -метод для кода объема выборки J
          

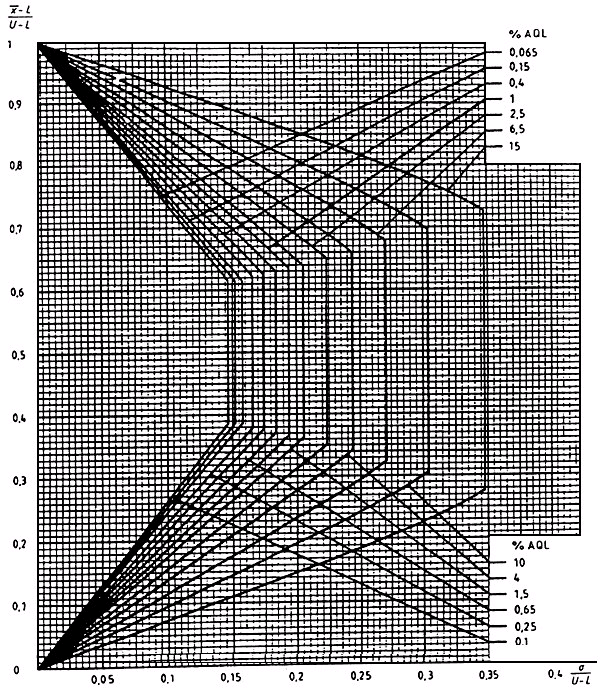
Диаграмма -К - Кривые приемки для предельных значений с общим уровнем качества: - метод для кода объема выборки К
          

Диаграмма -L - Кривые приемки для предельных значений с общим уровнем качества: -метод для кода объема выборки L
          

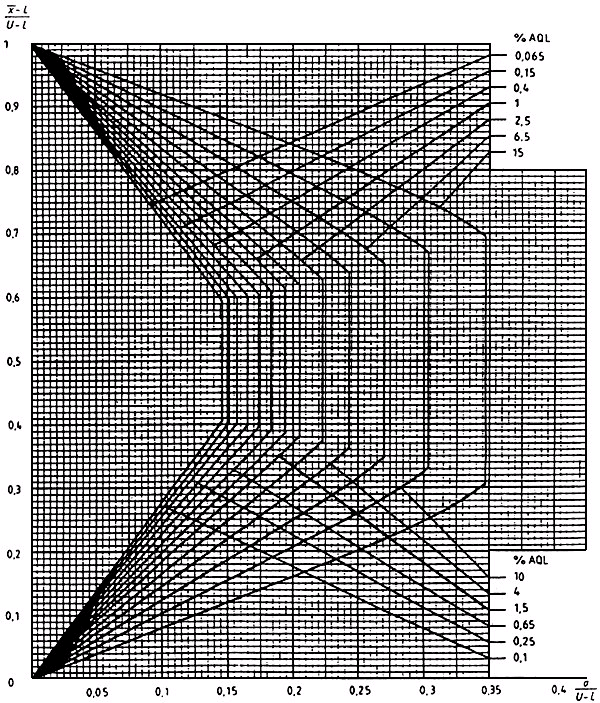
Диаграмма -М - Кривые приемки для предельных значений с общим уровнем качества: -метод для кода объема выборки М
          

Диаграмма -N - Кривые приемки для предельных значений с общим уровнем качества: -метод для кода объема выборки N
          

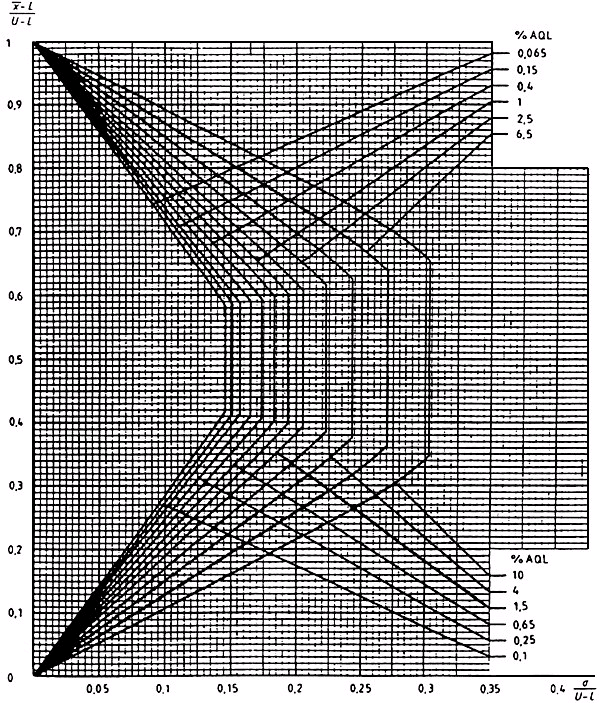
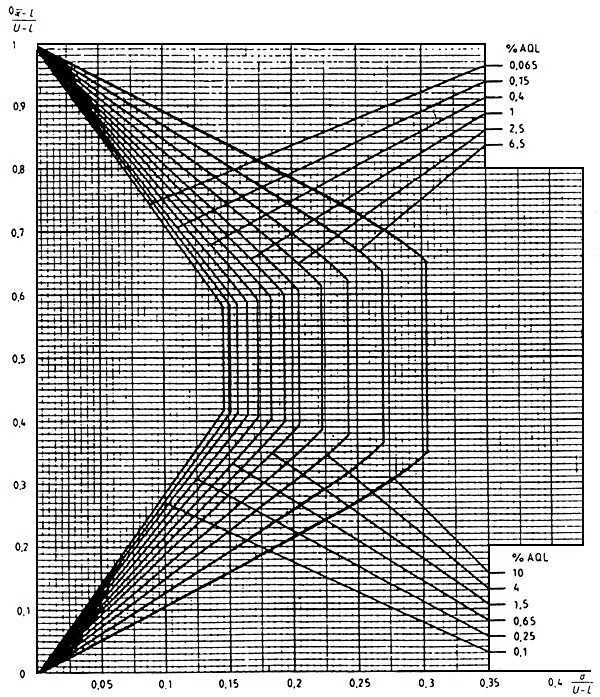
Диаграмма -P - Кривые приемки для предельных значений с общим уровнем качества: -метод для кода объема выборки P
          

ПРИЛОЖЕНИЕ А
(обязательное)

Процедуры получения  и  

     А.1 Процедуры получения
     
     А.1.1 Оценка стандартного отклонения партии по выборке обозначается символом . Значение величины  рассчитывают по формуле
     

,

     
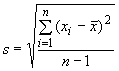где  - измеренное значение характеристики -й единицы в выборке объемом  изделий;

      - среднее арифметическое значений , то есть:

.

     
     А.1.2 Приведенная выше формула расчета  не рекомендуется для вычисления, так как расчеты можно упростить путем вычитания из  произвольного целого числа  и использования следующей эквивалентной формулы:
     

.

     
     Пример - Возьмем измерения, приведенные в примере к 14.6 настоящего стандарта. Принимаем =65 и представляем расчеты в виде таблицы:
     

     
     А.1.3 При наличии калькулятора величину  в А.1.2 можно принять равной нулю, тогда формула приобретет вид:
     

.

     
     На персональном компьютере можно одновременно получить кумулятивную сумму и для  и для , так что нет необходимости записывать отдельные значения  и . Но в следующем примере эти значения приведены для того, чтобы проиллюстрировать процесс. Заметьте, какими большими могут стать числа в четвертом столбце, и при использовании электронного калькулятора убедитесь, что он не отбрасывает цифры. Данные взяты из примера, приведенного в С.9.2.5 приложения С. Далее необходимо рассчитать .
     

     Таким образом, среднее =510,2, а оценка стандартного отклонения партии =21,43.
     
     А.1.4 Если изменения показаний измерительного прибора невелики, можно упростить арифметические вычисления, принимая в расчет только ту часть измерения, которая изменяется от изделия к изделию; например, если  имеет значения 27,515; 27,491; 27,479 и т.д., их следует учитывать, как если бы  был равен 515; 491; 479 и т.д. Поставив эти цифры в предыдущий пример, получаем =27,510 и s=0,021.
     
     А.1.5 Уравнению для  можно придать и другие формы. В зависимости от типа калькулятора можно использовать одну из следующих формул:

     
или
     

.

     
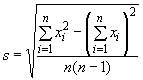     А.2 Процедура получения
     
     А.2.1 Если окажется, что значения  (или ) находятся в состоянии статистической управляемости, можно предположить, что  - это корень из среднего значения квадрата  (среднее взвешенное) (или ), получим
     

,

     
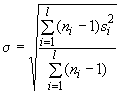где  - число партий;
     
      - объем выборки из -й партии;
     
      - значение выборочного стандартного отклонения для -й партии.
     
     А.2.2 Если объем выборки для каждой партии один и тот же, то вышеприведенная формула сводится к следующей:
     

.

     
     А.2.3 В случае -метода величина  в вышеприведенных выражениях должна быть заменена на , где  - средний размах;  - коэффициент масштаба для выборки из -й партии.
     
     

ПРИЛОЖЕНИЕ В
(обязательное)

Теоретическое обоснование

     
     В.0 Символы
     
     В данном приложении используются следующие обозначения:
     
      - общий процент или доля несоответствующих единиц продукции для процесса:
     

;

     
      - процент несоответствующих единиц, выходящий за нижний предел поля допуска;
     
      - процент несоответствующих единиц, выходящий за верхний предел поля допуска;
     
      - функция распределения;

     
      - параметр качества, равный  или минус ;
     
      - нормированное значение:
     

;

     
      - значение  для нижнего предела поля допуска:
     

;

     
      - значение  для верхнего предела поля допуска:
     

.

     
     B.1 Нормальное распределение
     
     В.1.1 Статистическая теория, на основе которой рассчитываются риски при контроле по количественному признаку, основана на свойствах нормального распределения, поэтому настоящий стандарт применим только там, где есть основание считать, что распределение измеряемой характеристики нормальное или близкое к нормальному.
     
     В.1.2 Нормальное распределение можно полностью определить через среднее  и стандартное отклонение  генеральной совокупности; если эти два параметра известны, можно рассчитать вероятность, с которой любое измеренное значение  попадет между двумя заданными значениями, а также вероятность, с которой любое измеренное значение выходит за установленные значения для верхнего или нижнего предела (рисунок 5).
     
     

Рисунок 5 - Нормальное распределение

     
     В.1.3 Чтобы облегчить сведение в таблицу этих вероятностей, измеренные значения  преобразуют в нормированную величину :
     

.

     
     Такой прием приводит все кривые нормального распределения к общему виду (рисунок 6), упрощает уравнение такой кривой и, поскольку общая площадь под кривой равна 1, позволяет построить одну таблицу, которая для данного значения z дает значение Р интегральной функции плотности вероятности нормального распределения (незаштрихованная площадь под кривой).
     

Рисунок 6 - Стандартное нормальное распределение

     
     
     В.2 Доля несоответствующих единиц продукции
     
     В.2.1 Доля несоответствующих единиц продукции представляет собой область (или области) под кривой функции распределения, находящуюся за пределом (или пределами) поля допуска.
     
     
     Примечание - Долю несоответствующих единиц продукции на практике часто выражают в процентах (см. разделы 1-4).
     
     
     В.2.2 Если распределение  нормальное, среднее  и стандартное отклонение  известны, то долю несоответствующих единиц  относительно заданных пределов характеристики  и(или)  можно определить по таблицам для нормального распределения как  и  (см. рисунок 7).
     

Рисунок 7 - Доля несоответствующих единиц продукции для постоянного =1 и
различных значений среднего () по отношению к заданному нижнему пределу поля
допуска характеристики качества

     
     
     В.3 Параметр качества

     
     В.3.1 Преобразовав исходное нормальное распределение к распределению с параметрами =0, =1, получим, что доля несоответствующих единиц однозначно определяется величиной
     

.

     
     В.3.2 Параметр качества для предельного значения поля допуска, полученный подобным образом, может быть использован в приемочном контроле вместо доли несоответствующих единиц продукции. Для верхнего предела поля допуска  параметр качества  определяется по формуле
     

,

     
     и для нижнего предела поля допуска  параметр качества  определяется по формуле
     

.

     
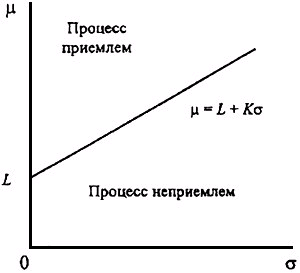
     В.4 Область приемлемости для односторонних и двусторонних пределов поля допуска
     
     При рассмотрении непрерывной серии партий AQL - это уровень качества, который при выборочном контроле служит границей удовлетворительного среднего уровня качества процесса и выражается в процентах несоответствующих изделий.
     
     При рассмотрении одностороннего или двустороннего допуска можно установить связь AQL с параметром качества . Так как существует взаимооднозначное соответствие между областью вне пределов поля допуска и параметром качества, можно ввести контрольный норматив  как нижнюю границу параметра качества  - приемлемости процесса при приемочном контроле, то есть процесс приемлем, если .
     
     Таким образом задается:
     
     - альтернативный показатель AQL;
     
     - значение константы .
     
     Для заданного множества значений пределов поля допуска pL или pU, зависящих от  и , на плоскости в координатах () должна быть область, где  (или ) меньше или равно AQL, которая является зоной приемлемости процессов. И наоборот, должна быть другая область, где  (или ) больше AQL, которая является зоной неприемлемости. Эти области можно разделить одной прямой линией.
     
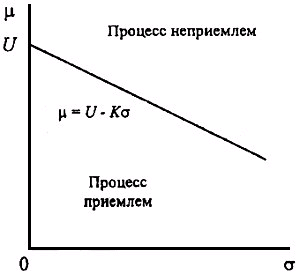
     Для нижнего одностороннего предела допуска график AQL в координатах ()задается зависимостью     

     
     или
     

.

     
     Для всех точек плоскости выше этой прямой средний процент несоответствующих единиц продукции меньше или равен AQL и, следовательно, процесс приемлем. Для точек ниже этой прямой он больше AQL и, следовательно, процесс неприемлем (рисунок 8).
     
     Для верхнего одностороннего предела поля допуска могут быть получены аналогичные соотношения:     

     
     или
     

.

     
     Для точек, расположенных под этой линией, средний процент несоответствующих единиц процесса меньше AQL и, следовательно, процесс приемлем, над этой линией - неприемлем (рисунок 9).
     

     Двустороннему допуску соответствует рисунок 10.
     

Рисунок 10 - Приемочная карта для двустороннего допуска ( и  известны)

     
     
     В.5 Область приемлемости для предельных значений с общим уровнем качества
     
     В.5.1 Пределы двустороннего допуска с общим AQL
     
     Если заданы верхнее и нижнее предельные значения с общим уровнем качества, допуск называется двусторонним допуском с общим уровнем качества. Задание общего уровня качества не позволяет отдельно получить доли несоответствующих единиц продукции  и  для верхнего и нижнего пределов поля допуска. Вместо этого устанавливают их сумму , которая не должна быть превышена.
     
     Иначе не существует способа получить график зависимости одного параметра, такого как , соответствующего AQL. Вместо этого для нахождения пары значений (, ), для которой доля несоответствующих единиц равна AQL, следует использовать математическое соотношение между величинами  и  и общей долей несоответствующих единиц процесса.
     
     Для данного значения  не только  и  зависят от , но и их сумма  также зависит от значения  относительно  и  (рисунок 11). Значение  достигает минимума, когда  находится посередине между  и , и возрастает, когда  отклоняется от середины.
     
     

Рисунок 11 - Влияние изменения  на долю несоответствующих единиц процесса (при постоянном значении )

     
     
     Площадь под кривой, находящаяся за пределами поля допуска для данной функции распределения при фиксированном значении  определяется величиной  (рисунок 12).
     
     

Рисунок 12 - Влияние изменения  (при постоянном ) на долю несоответствия процесса

     
     
     В.5.2 Максимальное стандартное отклонение процесса (MPSD)
     
     Наибольшее значение , которое возможно при данном AQL и , расположенном посередине между  и , можно рассматривать как максимальное стандартное отклонение процесса (MPSD) при нормальном контроле. Если  процесса больше значения этой величины, то доля несоответствующих единиц продукции в этом процессе больше AQL. Но обратное утверждение не всегда верно.
     
     При усиленном или ослабленном контроле MPSD - это максимальное стандартное отклонение процесса, при котором может быть обеспечен AQL на уровень ниже или выше соответственно.
     
     По усмотрению уполномоченной стороны величина  для усиленного контроля может быть использована для нормального или ослабленного контроля. При этой альтернативной процедуре выбор между - и s-методами не связан с правилами переключения.
     
     В.5.3 Кривая приемки
     
     Если даны предельные значения с общим уровнем качества, можно рассчитать ряд значений  и , дающих значения  и , в сумме равные AQL. Можно нанести эти значения на плоскость в координатах (,) и через эти точки провести кривую (рисунок 13). Эта кривая располагается внутри треугольника, соответствующего пределам двустороннего допуска, имеющего свои AQL (рисунок 10). Вблизи  и  эта кривая не отличима от прямой с наклоном минус К и плюс К соответственно, а затем она плавно изгибается, проходя через точку =MPSD и  (рисунок 13).
     

Рисунок 13 - Кривая приемки для р=AQL=10% для предельных значений с общим уровнем качества
в координатах (,)

     
     
     В.6 Выборочный контроль
     
     На практике значение  неизвестно, и его предстоит оценить на основании выборки; обычно также нужно оценить значение .
     
     Наилучшую оценку  дает среднее выборки . В зависимости от обстоятельств  либо принимается известным, либо оценивается по выборке одним из двух методов. Эти два подхода к определению  приводят к -методу, s-методу (и R-методу, приведенному в приложении С) для оценки партии.
     
     Используя оценки значений  и , получают оценку параметра качества . Она известна как статистика качества .
     
     Можно рассчитать значение контрольного норматива , которое для данного объема выборки и метода оценки стандартного отклонения процесса дает гарантию, что с заданной вероятностью партия приемлема, если статистика качества  больше или равна .
     
     В.7 -метод
     
     В.7.1 Получение контрольного норматива
     
     В определенных условиях, то есть когда процесс протекает в течение некоторого времени и с применением статистического контроля качества,  принимают известным и постоянным.
     
     Значения средних последовательных партий не считают постоянными или известными, поэтому каждое значение следует оценить через среднее случайной выборки единиц продукции, взятой от партии.
     
     Среднее выборки  необязательно равно среднему генеральной совокупности , но статистика  распределена нормально со средним =0 и стандартным отклонением, равным 1, так что можно показать, что для данной вероятности разность среднего выборки и среднего партии не превышает определенного значения величины.
     
     Например, для вероятности 95% это будет ±1,96.
     
     Формулу для верхней статистики качества  можно записать в другом виде:
     

.

     
     Первый член в правой части - постоянный, а второй - нормированное отклонение среднего. Поэтому  (как и ) также имеет нормальное распределение со стандартным отклонением, равным 1. Следовательно, можно так рассчитать , чтобы для данных объема выборки и AQL статистический показатель качества для выборки был с заданной вероятностью больше или равен , если партия приемлема.

     
     В.7.2 Критерии приемлемости для одностороннего или двустороннего допуска
     
     Для значения контрольного норматива , рассчитанного по В.7.1 и приведенного для нормального, усиленного и ослабленного контроля в таблицах IIIA, IIIB и IIIC соответственно, критерий приемлемости для одностороннего допуска приобретает вид:
     
     для верхнего предела поля допуска
     
     партия принимается, если ;
     
     для нижнего предела поля допуска
     
     партия принимается, если ;
     в других случаях партия не принимается.
     
     Если задан двусторонний допуск, то критерий приемлемости имеет вид:
     
     партия принимается, если  и ;
     
     партия не принимается, если  или .
          
     Так как значение  известно, на практике удобнее преобразовать критерии приемлемости, придав им следующий вид:  - для верхнего предела и  - для нижнего предела, так как правую часть этих критериев можно определить заранее.
     
     В.7.3 Критерии приемлемости для пределов двустороннего допуска с общим AQL
     
     Если даны пределы двустороннего допуска с общим AQL, то для того, чтобы принять решение о приемлемости партии, точку с координатами

     
можно нанести на соответствующую диаграмму (см. раздел 4 настоящего стандарта, диаграммы, начиная с -С до -Р), в соответствии с В.5.3. Так как  известна, эта точка будет лежать на вертикали, соответствующей этому значению . Поэтому на практике достаточно получить  и - приемлемые верхний и нижний пределы приемки  (рисунок 14).
     

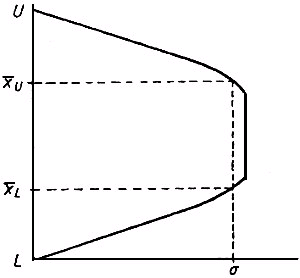
Рисунок 14 - Приемочная карта для предельных значений с общим уровнем качества

     
     
     Критерии приемлемости приобретают вид:
     
     партия принимается, если  и ;
     
     партия не принимается, если  или .
     
     В.8 -метод
     
     В.8.1 Получение контрольного норматива
     
     Когда и среднее, и стандартное отклонение генеральной совокупности неизвестны, их оценивают по выборке, взятой из этой совокупности. В -методе вместо  и  генеральной совокупности берут среднее  и стандартное отклонение , полученное из выборки по формуле
     

.

     
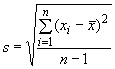     Таким образом,
     

 или .

     
     По сравнению с -методом это увеличивает вероятность ошибки, так как установлено, что при подстановке  вместо  в выражение  (В.7.1) величина , которую можно записать в виде
     

,

     
уже не имеет нормального распределения, а имеет -распределение с (-1) степенями свободы. Например, если =10, то с вероятностью 95% разность среднего выборки и среднего партии не превысит значения, равного , по сравнению с , приведенным в В.7.1.
     
     Далее,
     

,

     
что можно записать в виде
     

.

     
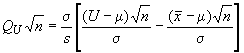     Далее находим
     

,

     
что можно записать в виде
     

.

     
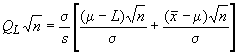     Эти статистики не являются нормально распределенными, а подчиняются нецентральному -распределению.
     
     Контрольный норматив  рассчитан с использованием нецентрального -распределения для стандартного диапазона объемов выборок и AQL и приводится в таблицах IIА, IIB и IIС для нормального, усиленного и ослабленного контроля соответственно.
     
     В.8.2 Критерии приемлемости для одностороннего и двустороннего допуска
     
     Критерии приемлемости по В.6 подобны приведенным в В.5, но с подстановкой значений оценок среднего, стандартного отклонения и статистики качества, полученных на выборке, и сравнением статистики качества с контрольным нормативом , рассчитанным для этого метода.
     
     Критерий приемлемости для одностороннего допуска имеет вид:
     
     партия принимается, если  или ;
     
     партия не принимается, если  или .
     
     Для двустороннего допуска критерий приемлемости имеет вид:
     
     партия принимается, если и , и ;
     
     партия не принимается, если либо , либо .
     
     Графический метод, показанный на рисунках 8, 9 и 10, также применим к обоим критериям. Пример приведен в 14.3 и показан на рисунке 2 настоящего стандарта.
     
     Верхняя граница зоны приемки по верхнему пределу поля допуска задается прямой линией , нижняя граница по нижнему пределу - прямой линией . Если заданы верхний и нижний пределы поля допуска, зоной приемки является область между этими двумя линиями и осью , как показано на рисунке 2 настоящего стандарта.
     
     В.8.3 Критерии приемлемости для двустороннего допуска с общим AQL
     
     В разделе В.5.3 показано, что если заданы пределы поля допуска с общим AQL, приемлемость процесса зависит от того, располагается ли точка (, ) внутри соответствующей кривой приемки на диаграмме приемки (см. рисунок 13).
     
     Определить приемлемость партии можно, нанеся полученные на основе выборки значения  и  на подобную диаграмму приемки с соответствующими объемом выборки и AQL.
     
     Кривые приемки для стандартных планов, приведенных в настоящем стандарте, рассчитаны с учетом неопределенности, вносимой при использовании оценок  и  для  и  соответственно в -методе.
     
     Эти кривые приведены в разделе 4 на диаграммах, начиная с s-D по s-P. Они приведены к единому масштабу, то есть вместо координат  и  при использовании s-метода применяются координаты
     

 и .

     
     Область приемки для кодов В и С (то есть для объемов выборки 3 и 4) ограничена четырьмя прямыми - осью ; прямой ; прямой, параллельной оси , проходящей через MSSD, (таблица IVs), и прямой , где значение  определяют по таблицам IIА, IIВ или IIС.
     
     Критерий приемлемости имеет вид:
     
     партия принимается, если точка  лежит внутри зоны приемки;
     
     партия не принимается, если точка лежит вне этой зоны.
     
     На практике при контроле серии партий задача контролера облегчается, если для установленного плана выборочного контроля создается специальная кривая приемки в координатах  и  (рисунок 3), как для нормального, так и для усиленного контроля.
     
     Если  больше MSSD (полученное по таблице IV), партия должна быть отклонена (сравни с В.5.2).
     
     В.8.4 Комбинированные пределы поля допуска
     
     Если задаются комбинации указанных выше типов пределов поля допуска, например AQL (соответствующий контрольному нормативу ) для верхнего предела в сочетании с общим AQL, то на приемочной карте строятся предельные линии или кривые, а зоной приемки является область, общая для обоих условий (рисунок 15).
     

Рисунок 15 - Карта приемки для комбинированных пределов поля допуска (s-метод)
     

     
ПРИЛОЖЕНИЕ С
(обязательное)

Планы выборочного контроля. R-метод

     С.1 Цель
     
     Этот метод создает альтернативу s-методу, приведенному в разделе 14 настоящего стандарта
     
     С.2 Определения
     
     При применении этого метода используются следующие дополнительные термины:
     
     С.2.1 R-метод: Метод определения приемлемости партии через оценку стандартного отклонения, основанную на среднем размахе измерений показателя качества в подгруппах выборки.
     
     С.2. 2 подгруппа: Пять единиц продукции, взятых в том порядке, в котором они подвергались измерению.
     
     С.2.3 размах (R): При использовании R-метода смысл этого понятия ограничен, а именно: размах для подгруппы.
     
     Примечание - В своем обычном значении размах - это разность между наибольшим и наименьшим наблюдаемыми значениями величин.
     
     
     С.2.4 средний размах (): Среднее значение размахов в подгруппах. Для выборок менее чем из десяти единиц за  принимают размах для всей выборки.
     
     С.2.5 максимальный средний размах (MAR): Наибольший, приемлемый в данных условиях, средний размах.
     
     С.3 Обозначения
     
     Для этого метода используются следующие дополнительные обозначения:
     
      - коэффициент масштаба для определения  по , приведенный в таблице RI настоящего приложения;
     
      - коэффициент, приведенный в таблице RI и представляющий собой отношение максимального среднего размаха к разности  и ;
     
      - контрольный норматив;
     
      - размах для подгруппы;
     
      - средний размах на основе данных по нескольким подгруппам.
     
     С.4 Теоретические основы
     
     R-метод обеспечивает альтернативный способ оценки стандартного отклонения.
     
     Для выборок малого объема величины  и , рассчитанные для одной и той же нормальной выборки, сильно коррелированны, что позволяет использовать  в качестве оценки для s. Эту взаимосвязь используют, когда работают с выборками, в которых меньше чем по десять изделий. С увеличением объема выборки величина R становится менее точной оценкой и ее не следует использовать в качестве оценки s. Но если эту выборку произвольно разбить на небольшие подгруппы одинакового объема, то средний для них размах  можно использовать для оценки стандартного отклонения партии.
     
     В стандартных планах для R-метода объемы выборок кратны пяти, за исключением трех планов, в которых объем выборок составляет 3, 4 и 7. Выборку разбивают на подгруппы по пять изделий, определяют размах R в каждой подгруппе и получают таким образом средний размах . Если в выборке менее 10 изделий, ее не разбивают на подгруппы, а размах используют, как если бы это был средний размах.
     
     Коэффициент масштаба рассчитывают исходя из объема подгруппы и количества подгрупп, так что s можно заменить выражением . В таблице RI приведен коэффициент масштаба  для различных объемов выборок на основе используемых в настоящем стандарте объемов подгрупп.
     
     Однако нет необходимости в использовании коэффициента масштаба , приведенного в таблице RI, так как для упрощения вычислений для R-метода создан специальный набор таблиц. В этом случае верхняя и нижняя статистики качества определяются непосредственно из формул:
     

 и .

     
     В таблице RI дается также сравнение кодов объема выборок для R-метода, s-метода и контроля по альтернативному признаку по ГОСТ Р 50779.71. Объем выборки для R-метода несколько больше, чем для s-метода, и в обоих случаях меньше, чем для метода контроля по альтернативному признаку.
     
     С.5 Критерий приемлемости
     
     Контрольный норматив  для каждого плана контроля вычисляют так, что критерии приемлемости для верхнего предела одностороннего допуска имеют вид:
     
     партия принимается, если ,
     
     для нижнего предела одностороннего допуска:
     
     партия принимается, если ,
     
     в других случаях партия не принимается.
     
     Если задан двусторонний допуск, критерии приемлемости таковы:
     
     партия принимается, если и  и ;
     
     партия не принимается, если либо , либо .
     
     Подставив  вместо , можно применить графический метод по 14.3 настоящего стандарта.
     
     Если задан двусторонний допуск с общим AQL, точку

     
     наносят на соответствующую диаграмму (R-D - R-P), чтобы установить, приемлема ли партия. Следует обратить внимание, что в R-методе эквивалентом максимального выборочного стандартного отклонения MSSD является максимальный средний размах MAR. Его значение можно найти в таблице RIV по объему выборки и AQL. Точка [=MAR; ] образует пик кривой приемки. Если значение величины  больше MAR, партия не принимается.
     
     С.6 Оперативная характеристика
     
     Оперативные характеристики, рассчитанные для s-метода, применимы и к R-методу, но дают несколько меньшую точность. Выбирают их по коду объема выборки и значению AQL.
     
     С.7 Контрольные карты
     
     Регистрация данных в форме контрольных карт, рекомендованная в 18.1 настоящего стандарта, в равной степени применима и к R-методу.
     
     Если задан двусторонний допуск с общим AQL, на R-карту следует наносить MAR.
     
     Если оказывается, что  стабилен, то корень из средневзвешенных значений квадратов значений величин  можно предположить равным , и тогда множитель  берут из таблицы RI. В этом случае, а также если получено разрешение на переход к этому методу от уполномоченной стороны, применим -метод (А.2, приложение А).
     
     С.8 Выбор метода
     
     Если имеется калькулятор, рекомендуется использовать s-метод, но если расчет s для этого метода создает трудности, то в качестве альтернативы этому методу можно использовать R-метод.
     
     R-метод прост для расчета, но требует некоторого увеличения объема выборки.
     
     С.9 Работа с планом выборочного контроля по R-методу
     
     С.9.1 Получение плана контроля
     
     Проверьте сначала, что приведенные в разделе 13 настоящего стандарта рекомендации выполнены.
     
     Стандартная процедура для выбора плана по R-методу такова:
     
     a) исходя из заданных уровня контроля (как правило, уровень контроля II) и объема партии, необходимо определить по таблице IA код объема выборки;
     
     b) используя заданный AQL, необходимо определить по таблице RIIA настоящего приложения объем выборки  и контрольный норматив .
     
     С.9.2 Работа с планом контроля
     
     С.9.2.1 Отберите в случайном порядке отдельные единицы выборки и измерьте в них контролируемый параметр. Результаты измерений запишите в том же порядке.
     
     С.9.2.2 Найдите сумму  всех измеренных значений и, поделив ее на  - количество изделий в выборке, получите выборочное среднее
     

.

     
     С.9.2.3 Получение значения величины :
     
     a) если изделий 10 или более, разбейте данные в порядке выполнения измерений на подгруппы по 5 (это всегда возможно, так как по стандартным планам количество изделий в выборках большого объема кратно пяти). Путем вычитания наименьшего измерения из наибольшего, получите размах измерений в каждой подгруппе, а затем подсчитайте средний размах ;
     
     b) выборки менее чем из 10 изделий на подгруппы не делят, разность наибольшего и наименьшего значений дает размах, который затем используют как средний размах .
     
     С.9.2.4 Применение критерия приемки
     
     Если заданы односторонний или двусторонний допуски, рассчитайте статистику качества  по формулам:

     
и (или)

.

     
     Сравните статистику качества [ и(или) ] с контрольным нормативом [ и(или) ], взятым из таблицы RIIA для нормального контроля. Если статистика качества больше или равна значению , партия принимается, если меньше - нет. Таким образом, если задан только верхний предел поля допуска , то
     
     партия принимается, если ;
     
     партия не принимается, если .
     
     Если задан только нижний предел поля допуска , то
     
     партия принимается, если ;
     
     партия не принимается, если .
     
     Если заданы и , и  (значения  различны, AQL для пределов двустороннего допуска различны), то
     
     партия принимается, если и , и ;
     
     партия не принимается, если  или .
     
     Пример - Нижний предел поля допуска для электрического сопротивления некоторого элемента равен 580 Ом. Контролю подвергается партия из 100 изделий. Уровень контроля II, нормальный контроль с AQL=1%. По таблице IА находим код F. Таблица RIIA показывает, что требуемый объем выборки - 10, а контрольный норматив равен 0,073, Допустим, что значения сопротивления, полученные в выборке, располагаются в следующем порядке:
     
     первая подгруппа 610; 615; 629; 593; 617 дает R=629-593=36;
     
     вторая подгруппа 623; 589; 608; 591; 611 дает R=623-589=34.
     
     Необходимо определить соответствие критерию приемки.
     

     Партия соответствует критерию приемки, так как  больше .
     
     С.9.2.5 Если требуется построить критерий приемки на графике, то для одностороннего или двустороннего допуска надо провести прямую, представленную уравнением  (для верхнего предела), которая проходит через точку () с наклоном минус , и(или) прямую, представленную уравнением  (для нижнего предела), которая проходит через точку () с наклоном плюс , на миллиметровой бумаге, откладывая значения  по вертикальной оси и  - по горизонтальной. Этот график можно построить перед тем, как приступить к контролю серии партий (в соответствии с процедурой, приведенной в 14.3 для s-метода). Затем необходимо взять значения  и , полученные на основе результатов измерений в каждой выборке, и нанести точку (). Если эта точка попадает в зону приемки, партия принимается, если нет - не принимается.
     
     Пример - Используя данные, приведенные в предыдущем примере, отметим на оси  точку =580 и проведем через эту точку линию с наклоном =0,703. Эта линия проходит через точки (=10; =587), (=20; =594,1), (=40; =608,1) и т.д. Выбираем соответствующую точку и проводим прямую через нее и через (=0; =580), то есть через . Область над этой прямой образует зону приемки. Подсчитано, что  и  равны 35 и 608,6 соответственно. Отметим точку (=35; =608,6) на графике. Из рисунка 16 видим, что она располагается в зоне приемки и что партию можно принять.
     

Рисунок 16 - Графический метод для одностороннего допуска и предельных значений
с общим уровнем качества

     
     
     Если заданы предельные значения с общим уровнем качества, необходимо пользоваться графическим методом, если только  не больше, чем MAR по таблице RIV. В последнем случае партию можно сразу отклонить.
     
     По коду объема выборки выберем соответствующую диаграмму для R-метода. На этой диаграмме выберем кривую приемки, соответствующую заданному AQL.
     
     Скопируем на кальку эту кривую и ближайшую к ней кривую внутри ее (внутренняя кривая необходима, если потребуется переключиться на усиленный контроль), тогда область между этими двумя кривыми образует зону предупреждения.
     
     Вычислим значения
     

 и  

     
и нанесем их на кальку с этими кривыми.
     
     Если эта точка располагается вне зоны приемки, партия не принимается, в других случаях - принимается.     
     
     Примечание - Рабочую кривую удобнее было бы привести в такой шкале, чтобы можно было непосредственно наносить  и  (рисунок 17).
     

Рисунок 17 - Кривая приемки для кода Н, =25, AQL=4%, MAR=70,7: (R-метод)

     
     
     Пример - Допуск на сопротивление некоторого электроэлемента составляет (520±50) Ом. Контролю подвергается партия из 350 изделий. Используется уровень контроля II, нормальный контроль, AQL=4%. По таблице IA находим код F. Таблица RIIA показывает, что требуемый объем выборки - 25, а таблица RIV - что для MAR значение  равно 0,707, Предположим, что значения сопротивления в выборке получены в следующем порядке:
     
     Первая подгруппа - 515; 491; 479; 507; 543;
     
     (=543-479=64).
     
     Вторая подгруппа - 521; 536; 483; 509; 514;
     
     (=536-483=53).
     
     Третья подгруппа - 507; 484; 526; 552; 499;
     
     (=552-484=68).
     
     Четвертая подгруппа - 530; 512; 492; 521; 467;
     
     (=530-467=63).
     
     Пятая подгруппа - 489; 513; 535; 501; 529;
     
     (=535-489=46).
     

     
     Нормированные значения среднего выборки и среднего размаха наносят затем на график R-H, AQL=4% (рисунок 17). Если нанесенная точка располагается вне кривой приемки, партия отклоняется.
     
     Точка (0,588; 0,402) лежит внутри кривой приемки, значит партия принимается.
     
     С.10 Процедура непрерывного контроля
     
     При использовании R-метода применяется процедура, приведенная в разделах 16-22 настоящего стандарта для s-метода.
     

     
Таблица RI - Коды, объемы выборок и коэффициент масштаба: R-метод

     
Таблица RIIA - Одноступенчатые выборочные планы для нормального контроля (основная таблица): R-метод
          

Таблица RIIВ - Одноступенчатые выборочные планы для усиленного контроля (основная таблица): R-метод
          

Таблица RIIС - Одноступенчатые выборочные планы для ослабленного контроля (основная таблица): R-метод

Таблица RIV - Значения F для максимального среднего размаха (MAR): R-метод

Диаграмма R-D - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки D (объем выборки - 5)
     
     

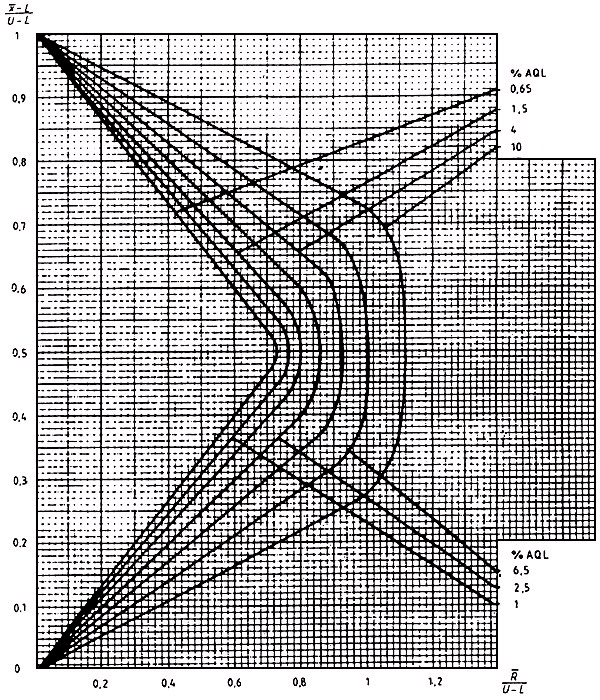
Диаграмма R-Е - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки Е (объем выборки - 7)
          

Диаграмма R-F - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки F (объем выборки - 10)
          

Диаграмма R-G - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки G (объем выборки - 15)
          

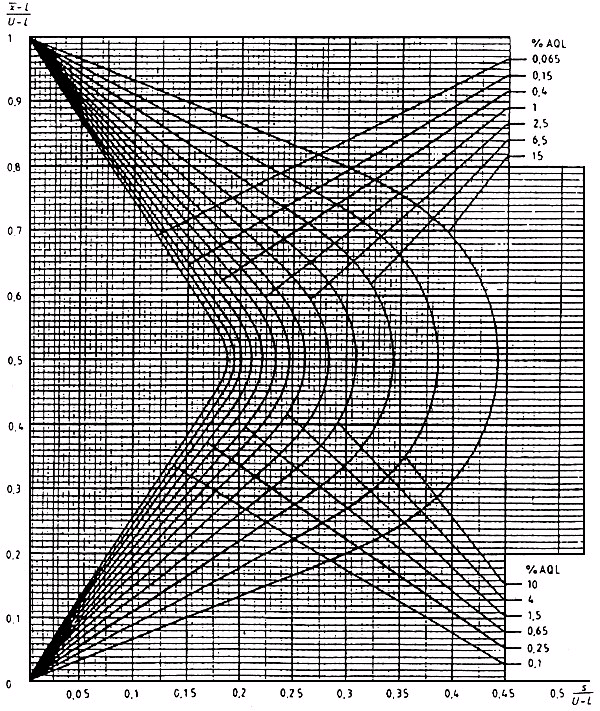
Диаграмма R-Н - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки Н (объем выборки - 20)
          

Диаграмма R-I - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки I (объем выборки - 25)
          

Диаграмма R-J - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки J (объем выборки - 40)
          

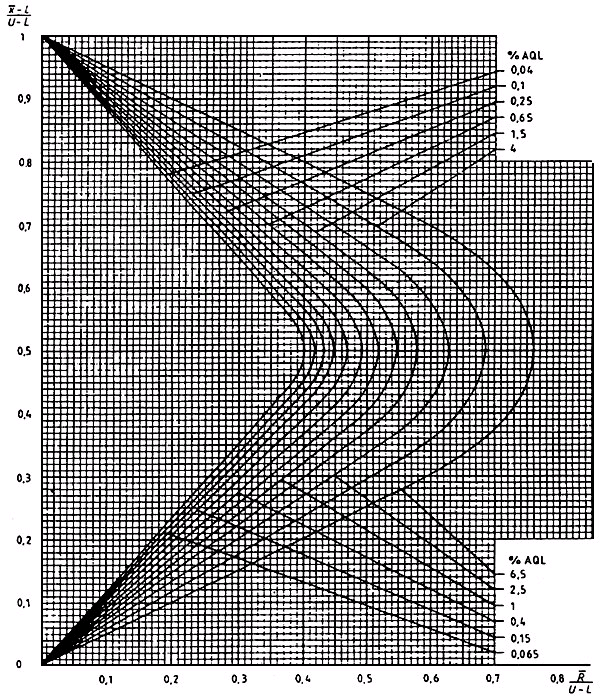
Диаграмма R-К - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки К (объем выборки - 60)     
     

Диаграмма R-L - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки L (объем выборки - 85)     
     

Диаграмма R-М - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки М (объем выборки - 115)
          

Диаграмма R-N - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки N (объем выборки - 175)
          

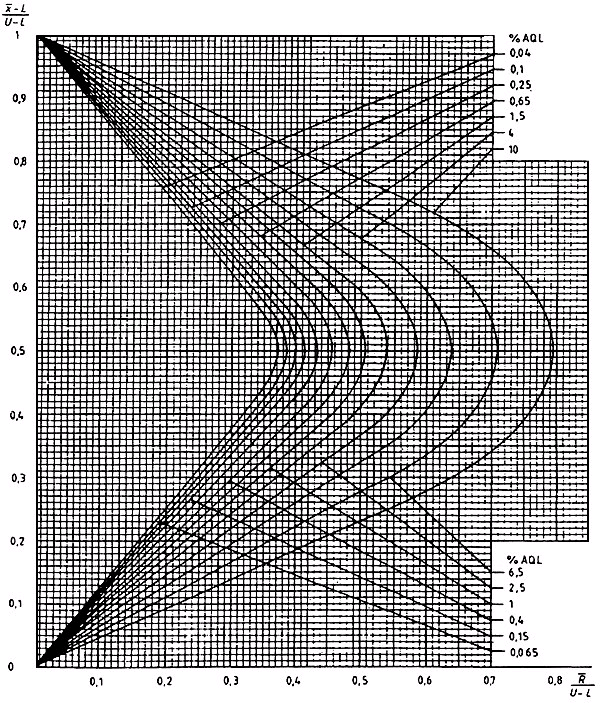
Диаграмма R-Р - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки Р (объем выборки - 230)
          

ПРИЛОЖЕНИЕ D
(обязательное)

Графическая бумага для s-метода

     Для того, чтобы приспособить систему кривых приемки s-метода для двустороннего допуска с общим AQL без изменения масштаба, производится специальная форма графической бумаги с уменьшенным масштабом (сжатым по горизонтали). Лист этой бумаги показан на рисунке 18.
     
     Если применяют выборочные планы s-метода для двустороннего допуска с общим AQL, соответствующие кривые приемки можно скопировать (или перенести на кальку) на фотокопию рисунка 18 (по 14.6).
     

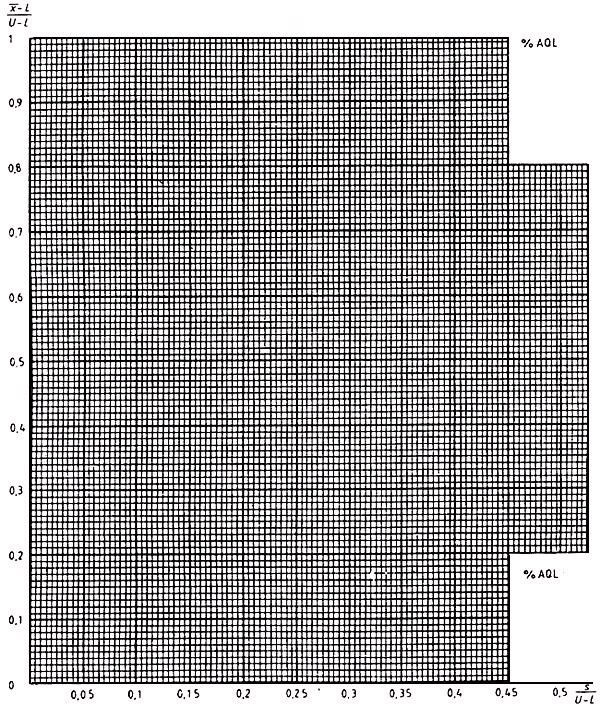
Рисунок 18 - Графическая бумага для s-метода

ПРИЛОЖЕНИЕ Е
(обязательное)

Взаимосвязь настоящего стандарта с
ГОСТ Р 50779.30, ГОСТ Р 50779.50, ГОСТ Р 50779.53

     Выбор планов контроля по настоящему стандарту основан на концепции AQL в отличие от концепции принципа распределения приоритетов (ПРП), использованной в ГОСТ Р 50779.30, ГОСТ Р 50779.50, ГОСТ Р 50779.53.
     
     При использовании концепции AQL нормируется значение приемлемого уровня качества (несоответствий) AQL, при котором партии будут приниматься с высокой вероятностью. Отклонение партий с более высоким уровнем несоответствий зависит от уровня контроля и может быть определено по оперативной характеристике плана контроля.
     
     При использовании концепции ПРП нормируется значение уровня качества (несоответствий) NQL, которое по определению является границей между удовлетворительным и неудовлетворительным качеством партий. При этом при контроле поставщика NQL играет роль браковочного уровня качества, а при контроле потребителя NQL играет роль приемлемого уровня качества AQL. Планы контроля поставщика и потребителя при этом различны, что обеспечивает практическое отсутствие спорных ситуаций (приемка партии у изготовителя и неприемка у потребителя). Планы контроля потребителя при этом близки к планам, выбираемым по концепции AQL.
     
     При заключении договора (между поставщиком и потребителем) и выборе стандарта для планов контроля следует иметь в виду следующие факторы:
     
     1) контроль по количественному признаку является более информативным и требует значительно меньших объемов выборок, чем контроль по альтернативному признаку, но требует знания закона распределения контролируемого показателя качества и более квалифицированного персонала;
     
     2) стандарты на основе концепции AQL предпочтительно применять для контроля, проводимого потребителем. При использовании соответствующих планов контроля у поставщика потребитель не будет иметь гарантии того, что поступающая к нему продукция имеет фактический уровень качества не хуже AQL. Соответствующие планы контроля достаточно хорошо отсеивают только продукцию с фактическим качеством значительно хуже AQL;
     
     3) планы контроля изготовителя по концепции ПРП дают потребителю уверенность в фактическом качестве полученной продукции не хуже NQL (уровень несоответствий - не выше NQL), но требуют, как правило, наличия "запаса по качеству" (более низкого фактического уровня несоответствий, чем NQL).
     
     

     
Текст документа сверен по:
официальное издание
М.: ИПК Издательство стандартов, 2000