- USD ЦБ 03.12 30.8099 -0.0387
- EUR ЦБ 03.12 41.4824 -0.0244
|
Краснодар:
|
погода |
Курсы
Индексы
- DJIA 03.12 12019.4 -0.01
- NASD 03.12 2626.93 0.03
- RTS 03.12 1545.57 -0.07
ГОСТ Р ИСО 9169-2006
Группа Т58
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
КАЧЕСТВО ВОЗДУХА
Определение характеристик методик выполнения измерений
Air quality. Determination of performance characteristics of measurement methods
ОКС 13.040
Дата введения 2007-08-01
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. N 184-ФЗ "О техническом регулировании", а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 "Стандартизация в Российской Федерации. Основные положения"
Сведения о стандарте
1 ПОДГОТОВЛЕН Открытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (ОАО "НИЦ КД") на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 457 "Качество воздуха"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 21 декабря 2006 г. N 323-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 9169:1994 "Качество воздуха. Определение характеристик методик выполнения измерений" (ISO 9169:1994 "Air quality - Determination of performance characteristics of measurement methods").
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении D
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе "Национальные стандарты", а текст изменений и поправок - в ежемесячно издаваемых информационных указателях "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
1 Область применения
Настоящий стандарт устанавливает процедуры количественного определения следующих характеристик методик выполнения измерений, используемых при оценке качества воздуха по ИСО 6879: систематической погрешности (частично), градуировочной характеристики, диапазона линейности, стабильности характеристик измерительной системы, предела обнаружения, периода необслуживаемой работы измерительной системы, селективности, чувствительности, верхнего предела измерений.
Установленные процедуры применимы только к измерительным системам с линейными* непрерывными градуировочными характеристиками, выходная переменная которых является величиной, усредненной за определенный промежуток времени. Результаты измерений, относящиеся к одному входному состоянию, предполагаются распределенными по нормальному закону. Преобразования промежуточных результатов в выходную переменную рассматриваются как составная часть работы измерительной системы.
______________
* Линейность может быть обеспечена путем последующей обработки первичной выходной переменной.
Для контроля стабильности измерительной системы при обычных условиях измерений достаточно исследовать поведение основных характеристик измерительной системы с использованием упрощенных испытаний. Приемлемая степень упрощения зависит от предварительного знания того, насколько эти характеристики стабильны во времени.
Если выходная переменная является усредненной по времени величиной, то нет существенного различия, является ли метод измерения инструментальным (автоматическим) или лабораторным (например, метод мокрой химии). Процедуры, установленные настоящим стандартом, распространяются на оба этих случая.
Установленные процедуры применяют при оценке качества воздуха на рабочем месте, внутри и вне помещений, а также при анализе выбросов загрязняющих веществ.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ИСО 3534-1:1993 Статистика. Словарь и условные обозначения. Часть 1. Термины, используемые в теории вероятности, и общие статистические термины
ИСО 5725-2:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
ИСО 6879:1995 Качество воздуха. Характеристики и соответствующие им понятия, относящиеся к методам измерений качества воздуха
3 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями.
Примечание - Используемый в настоящем стандарте термин "измерительная система" не требует какого-либо специального определения, а только указывает на инструментальную реализацию методики выполнения измерений.
3.1 период усреднения (averaging time),  : Установленный интервал времени, для которого характеристику качества воздуха считают представительной.
: Установленный интервал времени, для которого характеристику качества воздуха считают представительной.
Примечания
1 Каждый результат измерений является представительным для определенного интервала времени  , который превосходит некоторое минимальное значение, определяемое особенностями применяемой процедуры измерений. Чтобы иметь возможность сравнивать полученные оценки, относящиеся к сопоставляемым объектам, необходимо приведение этих оценок к единому установленному интервалу времени. Это достигается линейным усреднением без использования весовых функций.
, который превосходит некоторое минимальное значение, определяемое особенностями применяемой процедуры измерений. Чтобы иметь возможность сравнивать полученные оценки, относящиеся к сопоставляемым объектам, необходимо приведение этих оценок к единому установленному интервалу времени. Это достигается линейным усреднением без использования весовых функций.
Среднее значение для серии отдельных выборок при фиксированном 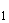 вычисляют по формуле
вычисляют по формуле
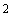 , (1)
, (1)
где 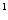 ;
;
 ,
,  .
.
Среднее значение для непрерывной выборки вычисляют по формуле
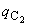 . (2)
. (2)
В обоих случаях исходная выборка 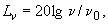 связана с представительным интервалом времени измерения
связана с представительным интервалом времени измерения 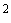 , тогда как усредненное значение
, тогда как усредненное значение 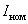 считается представительным для периода усреднения
считается представительным для периода усреднения 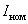 (предшествующего текущему значению
(предшествующего текущему значению  ).
).
Таким образом, период усреднения 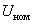 представляет собой заранее выбираемый единый интервал времени, в пределах которого оцениваемая переменная
представляет собой заранее выбираемый единый интервал времени, в пределах которого оцениваемая переменная 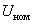 будет представительна (среднее квадратическое отклонение результатов измерений, относящихся к интервалам времени
будет представительна (среднее квадратическое отклонение результатов измерений, относящихся к интервалам времени  , для
, для 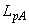 за период
за период 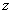 будет минимальным).
будет минимальным).
2 Усреднение может быть реализовано с помощью рекуррентной процедуры (выборочного усреднения).
3.2 система непрерывного измерения (continuously measuring system): Измерительная система, сигнал на выходе которой получен вследствие непрерывного воздействия на эту систему воздуха с определенной характеристикой его качества и является непрерывной функцией времени.
3.3 система дискретных измерений (non-continuously measuring system): Измерительная система, на выходе которой получают последовательность дискретных сигналов.
Примечание - Дискретность выходной переменной может быть следствием дискретности отбора проб или способа обработки данных измерительным устройством.
3.4 влияющая величина (influence variable): Переменная, влияющая на соотношение между истинными значениями исследуемой характеристики качества воздуха и соответствующими результатами измерений (например, на свободный член или угловой коэффициент градуировочной характеристики, или на степень разброса результатов измерений относительно градуировочной характеристики).
3.5 нормальные условия (reference conditions): Установленная совокупность значений (включая допустимые отклонения) влияющих величин, при которых получают представительные значения оцениваемой характеристики.
3.6 период необслуживаемой работы (period of unattended operation): Максимально допустимый интервал времени, в течение которого значения метрологических характеристик остаются в установленных пределах без технического обслуживания, например перезагрузки, калибровки* или регулировки.
______________
* Калибровку в Российской Федерации в данном случае принято называть градуировкой.
3.7 рандомизация (randomization): Случайное упорядочение объектов совокупности.
Примечания
1 Процедуру рандомизации можно представить следующим образом. Из совокупности, включающей 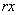 объектов (
объектов ( - натуральное число), изымают поочередно по одному объекту случайным образом (т.е. с равной вероятностью быть изъятым для каждого объекта) без возвращения и в порядке изъятия присваивают каждому объекту номер от 1 до
- натуральное число), изымают поочередно по одному объекту случайным образом (т.е. с равной вероятностью быть изъятым для каждого объекта) без возвращения и в порядке изъятия присваивают каждому объекту номер от 1 до  , получая, таким образом, упорядоченную последовательность объектов.
, получая, таким образом, упорядоченную последовательность объектов.
2 После выполнения процедуры рандомизации объекты совокупности называют рандомизированными (см. ИСО 3534-1).
3.8 случайная величина (random variable): Переменная, которая может принимать любое значение из заданного множества значений и с которой связано распределение вероятностей (см. ИСО 3534-1).
3.9 функция дисперсии (variance function): Зависимость дисперсии выходной переменной от исследуемой характеристики качества воздуха.
3.10 время установления рабочего режима (warm-up time): Минимальное время после включения, необходимое измерительному устройству для того, чтобы его характеристики достигли установленных значений (в отсутствие входного сигнала).
Примечания
1 На практике для определения времени установления рабочего режима контролируют изменения характеристики, для которой ожидаемый период стабилизации значений максимален.
2 В случае использования лабораторных методик применяют термин "время подготовки".
4 Обозначения и сокращения
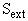 ,
, 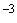 ,
, 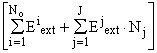 - коэффициенты модели функции дисперсии.
- коэффициенты модели функции дисперсии.
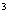 ,
, 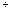 - оценки параметров градуировочной характеристики.
- оценки параметров градуировочной характеристики.
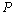 - характеристика качества воздуха.
- характеристика качества воздуха.
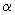 - значение
- значение 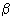 .
.
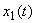 - оценка
- оценка 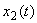 .
.
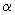 - значение
- значение 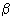 в
в 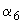 -й пробе (это может быть проба образца сравнения).
-й пробе (это может быть проба образца сравнения).
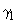 - нормирующий множитель для
- нормирующий множитель для 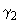 (в данном случае
(в данном случае 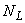 1).
1).
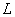 - погрешность оценки
- погрешность оценки 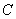 в точке
в точке 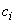 .
.
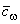 - взвешенное среднее (для набора весов
- взвешенное среднее (для набора весов 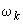 ).
).
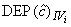 - зависимость (в первом порядке приближения) результата измерений
- зависимость (в первом порядке приближения) результата измерений 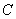 от
от 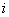 -й влияющей величины в точке
-й влияющей величины в точке 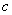 .
.
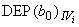 - зависимость (в первом порядке приближения) свободного члена градуировочной характеристики от
- зависимость (в первом порядке приближения) свободного члена градуировочной характеристики от 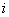 -й влияющей величины.
-й влияющей величины.
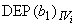 - зависимость (в первом порядке приближения) углового коэффициента градуировочной характеристики от
- зависимость (в первом порядке приближения) углового коэффициента градуировочной характеристики от 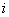 -й влияющей величины.
-й влияющей величины.
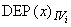 - зависимость (в первом порядке приближения) выходного сигнала от
- зависимость (в первом порядке приближения) выходного сигнала от 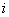 -й влияющей величины.
-й влияющей величины.
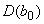 - дрейф (см. ИСО 6879) свободного члена градуировочной характеристики.
- дрейф (см. ИСО 6879) свободного члена градуировочной характеристики.
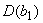 - дрейф углового коэффициента градуировочной характеристики.
- дрейф углового коэффициента градуировочной характеристики.
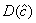 - дрейф результата измерений
- дрейф результата измерений 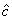 для
для 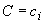 .
.
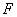 - статистика Фишера.
- статистика Фишера.
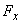 - квантиль уровня
- квантиль уровня 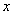
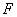 -распределения.
-распределения.
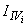 - селективность по отношению к
- селективность по отношению к 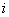 -й влияющей величине.
-й влияющей величине.
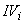 -
- 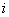 -я влияющая величина.
-я влияющая величина.
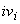 - значение
- значение 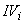 .
.
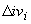 - разность значений
- разность значений 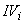 .
.
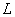 - общее число измерений при испытании на стабильность.
- общее число измерений при испытании на стабильность.
 - предел обнаружения.
- предел обнаружения.
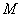 - общее число проб, полученных на основе образца сравнения в рамках одной калибровки.
- общее число проб, полученных на основе образца сравнения в рамках одной калибровки.
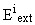 - число значений выходной переменной для
- число значений выходной переменной для 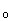 .
.
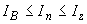 ,
, 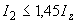 - оценка углового коэффициента регрессионной зависимости выходной переменной от времени при
- оценка углового коэффициента регрессионной зависимости выходной переменной от времени при 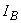 и
и 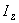 соответственно.
соответственно.
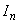 - разрешение в точке
- разрешение в точке 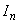 .
.
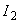 ,
, 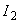 - пределы воспроизводимости и повторяемости (сходимости) соответственно.
- пределы воспроизводимости и повторяемости (сходимости) соответственно.
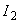 - оценка сглаженного стандартного отклонения
- оценка сглаженного стандартного отклонения 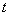 для
для 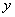 .
.
 - сглаженная оценка дисперсии
- сглаженная оценка дисперсии 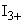 (повторных измерений) для
(повторных измерений) для 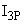 .
.
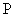 - нормирующий множитель для стандартного отклонения (в настоящем стандарте значение
- нормирующий множитель для стандартного отклонения (в настоящем стандарте значение  принято равным единице).
принято равным единице).
 ,
, 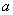 - оценка стандартного отклонения нестабильности (см. ИСО 6879) свободного члена и углового коэффициента линейной градуировочной характеристики соответственно.
- оценка стандартного отклонения нестабильности (см. ИСО 6879) свободного члена и углового коэффициента линейной градуировочной характеристики соответственно.
 - оценка стандартного отклонения нестабильности в точке
- оценка стандартного отклонения нестабильности в точке 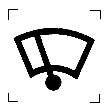 .
.
 - оценка стандартного отклонения экспериментально определенной градуировочной характеристики (в единицах измерения
- оценка стандартного отклонения экспериментально определенной градуировочной характеристики (в единицах измерения  ).
).
 - оценка стандартного отклонения экспериментально определенной градуировочной характеристики (в единицах выходной переменной).
- оценка стандартного отклонения экспериментально определенной градуировочной характеристики (в единицах выходной переменной).
 - оценка стандартного отклонения выборки
- оценка стандартного отклонения выборки  для
для  (
( - индекс выборки).
- индекс выборки).
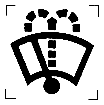 - сглаженная оценка стандартного отклонения выборки
- сглаженная оценка стандартного отклонения выборки  для
для 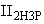 (
( - индекс выборки).
- индекс выборки).
 - оценка стандартного отклонения повторяемости (сходимости).
- оценка стандартного отклонения повторяемости (сходимости).
 - квантиль уровня
- квантиль уровня 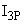
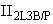 -распределения с
-распределения с  степенями свободы.
степенями свободы.
 - статистика для критерия Граббса.
- статистика для критерия Граббса.
 - выходная переменная.
- выходная переменная.
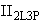 - значение
- значение  .
.
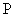 - оценка
- оценка  .
.
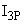 - оценка выходного сигнала для
- оценка выходного сигнала для  .
.
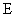 - среднее выборочное выходных сигналов для
- среднее выборочное выходных сигналов для  .
.
 - выходной сигнал в точке
- выходной сигнал в точке  с наибольшим абсолютным отклонением от
с наибольшим абсолютным отклонением от 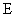 .
.
 -
-  -е значение выходного сигнала для
-е значение выходного сигнала для 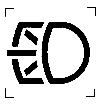 .
.
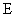 ,
,  -
- 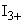 -е значения выходного сигнала, полученные при более высоком и более низком значениях
-е значения выходного сигнала, полученные при более высоком и более низком значениях  для образца сравнения соответственно.
для образца сравнения соответственно.
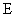 - взвешенное среднее всей последовательности выходных сигналов в рамках калибровки.
- взвешенное среднее всей последовательности выходных сигналов в рамках калибровки.
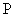 ,
,  - свободный член и угловой коэффициент линейной градуировочной характеристики, соответственно.
- свободный член и угловой коэффициент линейной градуировочной характеристики, соответственно.
 - время.
- время.
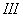 - число степеней свободы при калибровке.
- число степеней свободы при калибровке.
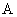 ,
,  - числа степеней свободы для оценок дисперсий, входящих в числитель и знаменатель статистики Фишера соответственно.
- числа степеней свободы для оценок дисперсий, входящих в числитель и знаменатель статистики Фишера соответственно.
 - непрерывная весовая функция, полученная на основе модели для
- непрерывная весовая функция, полученная на основе модели для  .
.
 - значение весового коэффициента в точке
- значение весового коэффициента в точке  .
.
5 Общие требования
5.1 Описание процедуры
Методика выполнения измерений включает в себя такие этапы как отбор проб, анализ, обработка результатов измерений, калибровка, каждый из которых должен быть детально описан. Схема последовательности этапов измерений и калибровки приведена на рисунке 1.
Примечание - При определенных обстоятельствах для оценки метрологических характеристик измерительной системы достаточно проверить выполнение одного или нескольких этапов. Кроме того, в ряде случаев выполнение всех этапов, соответствующих методу измерений, невозможно. Общей рекомендацией является выполнение максимально возможного числа этапов.
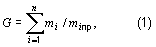
Рисунок 1 - Схема последовательности этапов измерения и калибровки
5.2 Определение исследуемых характеристик
Характеристики измерительной системы должны быть определены в порядке их влияния на окончательную оценку точности. Обязательным является определение коэффициентов уравнения градуировочной характеристики: свободного члена 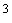 и углового коэффициента
и углового коэффициента 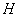 , а также оценок погрешности их определения. Допускается не определять характеристики, в отношении которых имеются априорные сведения, а также не исследовать влияющие величины, эффект воздействия которых компенсируется процедурой рандомизации.
, а также оценок погрешности их определения. Допускается не определять характеристики, в отношении которых имеются априорные сведения, а также не исследовать влияющие величины, эффект воздействия которых компенсируется процедурой рандомизации.
5.3 Условия проведения испытаний
Условия проведения испытаний должны быть точно установлены и являться типичными для измерений данной характеристики качества воздуха. При оценке статистических характеристик все определенные влияющие величины должны поддерживаться неизменными. При проверке чувствительности параметров функциональных зависимостей все влияющие величины за исключением той, чье влияние исследуют, должны также оставаться постоянными.
В настоящем стандарте все статистические оценки получают с доверительной вероятностью 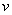 0,95.
0,95.
6 Процедуры испытаний
6.1 Период усреднения
Период усреднения должен быть таким, чтобы два последовательных выходных сигнала были статистически независимыми. Таким образом, минимальное значение периода усреднения определяется:
a) временем отклика - для систем непрерывного измерения;
b) временем отбора проб (временем заполнения, временем накопления и т.д.) - для систем дискретных измерений.
6.1.1 Системы непрерывного измерения
Для определения времени отклика, включающего время запаздывания (реакции измерительной системы на входное воздействие) и время установления (нарастания или спада) сигнала, исследуемую характеристику качества воздуха (функцию на входе измерительной системы) изменяют скачкообразным образом, например от 20% до 80% верхнего предела измерений (см. рисунок 2). Для достоверного определения временных характеристик указанную процедуру повторяют достаточное число раз. Если время нарастания и время спада отличаются, то время отклика принимают равным наибольшему из этих двух значений. Период усреднения должен превышать время отклика не менее чем в четыре раза.
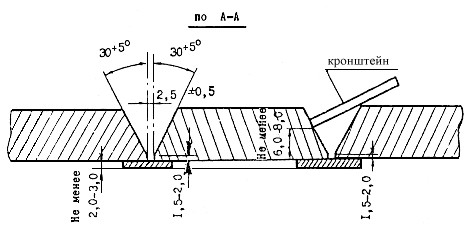
Рисунок 2 - Временные характеристики измерительной системы
6.1.2 Системы дискретных измерений
Период усреднения должен быть не менее максимального времени отбора проб (времени заполнения или накопления в зависимости от конкретного метода измерений).
6.2 Функциональные зависимости и статистические характеристики
Определяют характеристики:
a) относящиеся к градуировочной характеристике и ее стабильности в нормальных условиях;
b) относящиеся к зависимости градуировочной характеристики от влияющих величин.
Линейная градуировочная характеристика задается своим угловым коэффициентом (чувствительностью) и свободным членом. Нестабильность измерительной системы и действие влияющих величин определяют по изменениям свободного члена и углового коэффициента.
Все выходные сигналы, используемые в данном испытании, должны быть получены после достижения измерительной системой установившегося режима работы.
6.2.1 Калибровка
Процедура калибровки включает не менее десяти повторных измерений при не менее пяти различных значениях характеристики качества воздуха.
При наличии дрейфа характеристик продолжительность калибровки должна быть минимальной. Это может быть достигнуто последовательными снятиями показаний измерительного устройства при соответствующем значении характеристики качества воздуха, а затем после изменения характеристики и ее стабилизации последующим снятием показаний устройства (см. рисунок 3). Однако данная процедура применима только в отсутствие гистерезиса или если гистерезис незначителен.
Примечание - Повторения в условиях воспроизводимости (см. ИСО 5725-2) требуют случайной выборки из множества исследуемых влияющих величин (рандомизации).
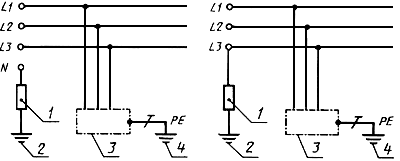
1 - усредненный выходной сигнал; 2 - несглаженный выходной сигнал; 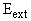 - значение выходного сигнала
- значение выходного сигнала
на 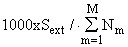 -м периоде усреднения для
-м периоде усреднения для 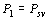 -го значения характеристики качества воздуха, полученного на основе
-го значения характеристики качества воздуха, полученного на основе
образца сравнения; 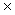 ,
, 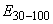 - периоды времени, исключаемые из рассмотрения
- периоды времени, исключаемые из рассмотрения
при проведении калибровки
Рисунок 3 - Пример калибровки
6.2.1.1 Исключение выбросов
Обычно опыт проведения измерений позволяет распознавать возможные выбросы. Для большей объективности этот опыт должен сочетаться с применением соответствующего критерия, например, критерия Граббса [1]. Такой критерий позволяет выявлять "подозрительные" результаты измерений, но не принимать в их отношении окончательных решений, поскольку аномально большие результаты измерений могут быть связаны не только с какими-либо сбоями в работе измерительной системы (когда их следует рассматривать как выбросы), но и быть обусловлены статистической природой сигнала.
Для выявления выбросов оценивают стандартное отклонение 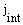 в точке
в точке 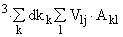 по формуле
по формуле
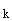 . (3)
. (3)
Для той же точки 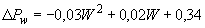 определяют значение выходного сигнала
определяют значение выходного сигнала 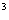 с наибольшим абсолютным отклонением от среднего значения
с наибольшим абсолютным отклонением от среднего значения 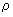 . Вычисляют статистику по формуле
. Вычисляют статистику по формуле
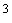 , (4)
, (4)
где
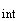 , (5)
, (5)
и сравнивают ее с критическим значением, взятым из таблицы значений двустороннего критерия Граббса (см. приложение А).
Если 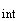 превышает критическое значение, то проверяют, может ли данный выброс быть обусловлен сбоем в работе измерительной системы, и если данное предположение находит подтверждение, то исключают этот выброс из совокупности результатов измерений. Данная процедура может быть повторена в отношении других "подозрительных" значений, однако если указанная проверка приводит к исключению более 5% значений выходных сигналов, то калибровку признают недействительной.
превышает критическое значение, то проверяют, может ли данный выброс быть обусловлен сбоем в работе измерительной системы, и если данное предположение находит подтверждение, то исключают этот выброс из совокупности результатов измерений. Данная процедура может быть повторена в отношении других "подозрительных" значений, однако если указанная проверка приводит к исключению более 5% значений выходных сигналов, то калибровку признают недействительной.
Если подозрения на сбой в измерительной системе не подтверждаются, то выбросы не исключают. В этом случае рекомендуется проверка исходных допущений, принятых при проведении калибровки.
6.2.1.2 Вычисление функции дисперсии
Функцию дисперсии используют при определении других характеристик измерительной системы. Поэтому вычисление функции дисперсии - необходимый этап калибровки.
Для каждого из значений характеристики качества воздуха 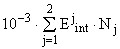 дисперсию
дисперсию 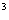 выходных сигналов
выходных сигналов 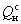 вычисляют по формуле
вычисляют по формуле
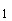 . (6)
. (6)
Предполагают, что для 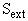 справедлива следующая модель (см. [2]):
справедлива следующая модель (см. [2]):
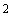 . (7)
. (7)
Коэффициенты полинома второго порядка относительно 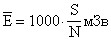 подбирают таким образом, чтобы аппроксимировать зависимостью (7) полученные экспериментальные значения:
подбирают таким образом, чтобы аппроксимировать зависимостью (7) полученные экспериментальные значения:
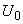 ;
;
 ; (8)
; (8)
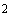 ,
,
где
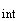 . (9)
. (9)
Параметры, входящие в формулу (8), получают заменой в 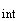
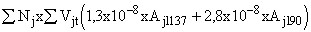 на
на 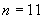 и
и 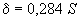 на
на 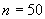 или
или 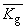 , соответственно, где
, соответственно, где
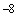 ; (10)
; (10)
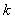 .
.
Пример функции дисперсии, полученной таким способом, приведен на рисунке 4.
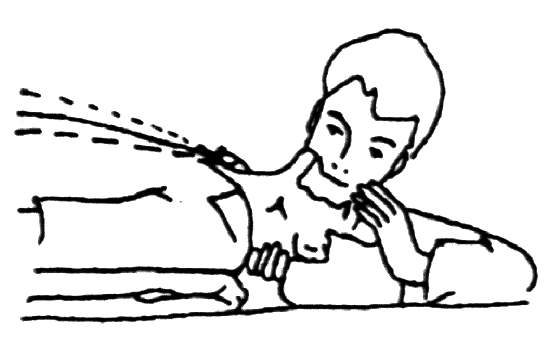
Рисунок 4 - График логарифма функции дисперсии
Таким образом, уравнение сглаженной функции дисперсии 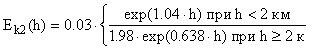 имеет вид
имеет вид
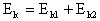 . (11)
. (11)
Используемый в дальнейшем при вычислении градуировочной характеристики весовой коэффициент 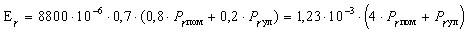 в точке
в точке 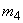 является выборочным значением весовой функции, которая обратно пропорциональна функции дисперсии:
является выборочным значением весовой функции, которая обратно пропорциональна функции дисперсии:
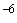 . (12)
. (12)
6.2.1.3 Вычисление градуировочной характеристики
Линейная градуировочная характеристика (см. [5])
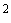 (13)
(13)
может быть приближенно оценена в виде
 , (14)
, (14)
где
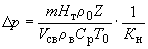 ;
;
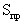 ; (15)
; (15)
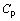 ;
;
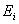 . (16)
. (16)
Дополнительным источником неопределенности, помимо той, что обусловлена взаимным разбросом относительно друг друга истинных значений результатов измерений и выходных сигналов, здесь является неопределенность самой модели.
Эта неопределенность может быть вычислена через стандартное отклонение (см. [2]) по формуле
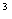 . (17)
. (17)
Иногда выходной сигнал получают после введения поправки на холостую пробу. Если холостая проба действительно соответствует отсутствию исследуемого загрязняющего вещества, то после внесения поправки градуировочная характеристика должна проходить через начало координат. В этом случае выражение для коэффициента 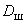 принимает вид
принимает вид
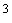 . (18)
. (18)
Стандартное отклонение 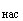 инвариантно по отношению к процедуре внесения поправки, но число степеней свободы при этом уменьшается на единицу:
инвариантно по отношению к процедуре внесения поправки, но число степеней свободы при этом уменьшается на единицу:
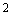 . (19)
. (19)
6.2.1.4 Вычисление аналитической функции
Вычисляют аналитическую функцию, которая является обратной градуировочной характеристике, по формуле
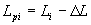 . (20)
. (20)
6.2.1.5 Линейность
Гипотезу о линейности градуировочной характеристики (см. рисунок 5) проверяют по критерию Фишера (см. [6]), для чего вычисляют статистику Фишера
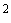 , (21)
, (21)
где 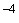 - число степеней свободы для оценки дисперсии в числителе формулы (21);
- число степеней свободы для оценки дисперсии в числителе формулы (21);
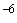 - число степеней свободы для оценки дисперсии в знаменателе формулы (21).
- число степеней свободы для оценки дисперсии в знаменателе формулы (21).
Если 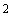 не превышает табулированного критического значения
не превышает табулированного критического значения 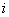 , полученного из
, полученного из 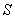 -распределения для одностороннего критерия при заданном уровне значимости
-распределения для одностороннего критерия при заданном уровне значимости 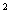 0,05 (см. приложение В), то нелинейность считают незначительной и соответствующие метрологические характеристики могут быть определены.
0,05 (см. приложение В), то нелинейность считают незначительной и соответствующие метрологические характеристики могут быть определены.
Если 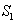 превышает критическое значение, то гипотезу о линейности отклоняют. В этом случае проверяют, является ли нелинейность существенным фактором по сравнению с другими источниками неопределенности, для чего проверяют выполнение условия
превышает критическое значение, то гипотезу о линейности отклоняют. В этом случае проверяют, является ли нелинейность существенным фактором по сравнению с другими источниками неопределенности, для чего проверяют выполнение условия
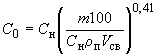 . (22)
. (22)
Если неравенство (22) выполнено (см. рисунок 5), то нелинейность можно не принимать во внимание и определять соответствующие метрологические характеристики. Если неравенство не выполнено, то процедура определения характеристик должна быть остановлена. В этом случае рекомендуется:
a) проверить качество проб, полученных на основе образцов сравнения, которые могут быть потенциальной причиной нелинейности;
b) если проверка проб не позволяет решить проблему, то определить область значений 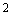 , для которых неравенство (22) не выполнено, и выяснить, входит ли в эту область исследуемый диапазон, или проверить, нельзя ли устранить нелинейность за счет соответствующего монотонного преобразования градуировочной характеристики;
, для которых неравенство (22) не выполнено, и выяснить, входит ли в эту область исследуемый диапазон, или проверить, нельзя ли устранить нелинейность за счет соответствующего монотонного преобразования градуировочной характеристики;
c) при выявлении возможности уменьшить нелинейность градуировочной характеристики определить новый метод измерений и все измерения для расчета метрологических характеристик провести заново.
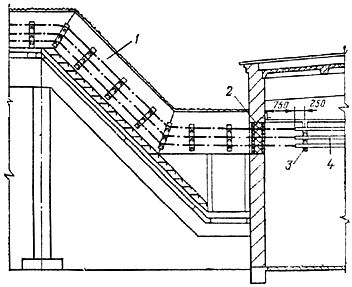
Рисунок 5 - График нелинейной градуировочной характеристики (гипотеза о линейности отклонена)
6.2.1.6 Неопределенность, связанная с оценкой градуировочной характеристики
Коэффициенты градуировочной характеристики 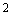 и
и 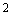 представляют собой оценки, полученные на основе ограниченного числа измерений. Эти оценки, в общем, не совпадают с истинными значениями, которые были бы получены в результате обработки генеральной совокупности. Соответственно
представляют собой оценки, полученные на основе ограниченного числа измерений. Эти оценки, в общем, не совпадают с истинными значениями, которые были бы получены в результате обработки генеральной совокупности. Соответственно 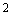 , полученная с использованием градуировочной характеристики (или аналитической функции), также будет отклоняться от истинного значения. Это отклонение будет изменяться случайным образом с каждой новой калибровкой.
, полученная с использованием градуировочной характеристики (или аналитической функции), также будет отклоняться от истинного значения. Это отклонение будет изменяться случайным образом с каждой новой калибровкой.
Неопределенность 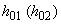 , полученной в результате калибровки, может быть вычислена (см. [3]) через
, полученной в результате калибровки, может быть вычислена (см. [3]) через 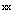 для соответствующего стандартного отклонения (см. 6.2.1.3) по формуле
для соответствующего стандартного отклонения (см. 6.2.1.3) по формуле
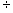 . (23)
. (23)
Для упрощенной двухуровневой калибровки в условиях применения, выполняемой в предположении, что метрологические характеристики остаются стабильными, можно использовать следующую приближенную формулу:
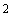 , (24)
, (24)
где оценки стандартного отклонения 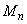 соответствуют следующим значениям
соответствуют следующим значениям 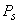 , полученным на основе образцов сравнения:
, полученным на основе образцов сравнения:
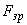 0 (холостая проба);
0 (холостая проба);
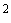 (максимальное значение
(максимальное значение 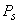 для заданного набора образцов сравнения).
для заданного набора образцов сравнения).
6.2.1.7 Прецизионность
6.2.1.7.1 Повторяемость
Повторяемость (сходимость) 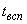 оценивают, определяя в условиях повторяемости (сходимости) функцию дисперсии (см. ИСО 5725-2).
оценивают, определяя в условиях повторяемости (сходимости) функцию дисперсии (см. ИСО 5725-2).
После определения сглаженной функции дисперсии 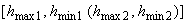 (см. 6.2.1.2) вычисляют стандартное отклонение повторяемости (сходимости) по формуле
(см. 6.2.1.2) вычисляют стандартное отклонение повторяемости (сходимости) по формуле
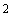 . (25)
. (25)
Предел повторяемости (сходимости) 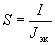 вычисляют по формуле
вычисляют по формуле
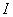 , (26)
, (26)
где 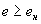 - табулированное значение
- табулированное значение 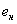 для двустороннего квантиля
для двустороннего квантиля 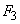 -распределения уровня
-распределения уровня  0,05 (см. приложение С) для
0,05 (см. приложение С) для 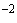 степеней свободы,
степеней свободы, 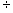 .
.
Примечание - Наличие коэффициента  в формуле (26) обусловлено тем, что
в формуле (26) обусловлено тем, что 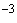 , так же как и
, так же как и 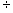 , по определению относится к разности результатов двух измерений.
, по определению относится к разности результатов двух измерений.
6.2.1.7.2 Воспроизводимость
Метод определения воспроизводимости - в соответствии с ИСО 5725-2.
6.2.1.8 Разрешающая способность измерительной системы
Разрешение измерительной системы при 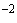 вычисляют по формуле
вычисляют по формуле
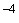 . (27)
. (27)
6.2.1.9 Предел обнаружения
Вычисляют дисперсию 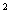 при
при 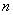 0 на основе функции дисперсии (см. 6.2.1.2). Тогда стандартное отклонение повторяемости (сходимости), в соответствии с 6.2.1.7, примет вид
0 на основе функции дисперсии (см. 6.2.1.2). Тогда стандартное отклонение повторяемости (сходимости), в соответствии с 6.2.1.7, примет вид
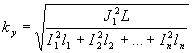 . (28)
. (28)
Для нормальных условий работы предел обнаружения вычисляют по формупе
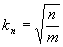 (
( и
и 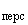 взяты для
взяты для  0). (29)
0). (29)
6.2.1.10 Верхний предел измерений
Верхний предел измерений принимают приблизительно равным значению характеристики качества воздуха, которая соответствует максимальному результату измерений, подтвержденному в процессе калибровки.
Примечание - Для методов, реализующих процесс усреднения сигнала, рабочий верхний предел измерений будет понижен за счет колебаний характеристики качества воздуха в пределах периода усреднения.
6.2.2 Нестабильность
В идеале метрологические характеристики не должны изменяться со временем. На практике, однако, такие изменения неизбежны. В то же время изменение, например, коэффициентов градуировочной характеристики  и
и  способно существенно повлиять на точность оценки измеряемой величины. Нестабильность, проявляющаяся в изменении коэффициентов за установленный период времени, может иметь систематическую составляющую (дрейф) и случайные отклонения (рассеяние) относительно этой систематической составляющей. Предполагается, что значение дрейфа остается постоянным, а стандартное отклонение, характеризующее рассеяние, равно стандартному отклонению повторяемости (сходимости) или превышает его.
способно существенно повлиять на точность оценки измеряемой величины. Нестабильность, проявляющаяся в изменении коэффициентов за установленный период времени, может иметь систематическую составляющую (дрейф) и случайные отклонения (рассеяние) относительно этой систематической составляющей. Предполагается, что значение дрейфа остается постоянным, а стандартное отклонение, характеризующее рассеяние, равно стандартному отклонению повторяемости (сходимости) или превышает его.
Характеристики дрейфа и рассеяния получают, строя линейную регрессионную зависимость выходной переменной от времени. Интервал времени между отсчетами выходной переменной обусловлен задачей измерений (см. рисунок 6). Дрейф характеризуется наклоном линии регрессии, а рассеяние - стандартным отклонением остатков.
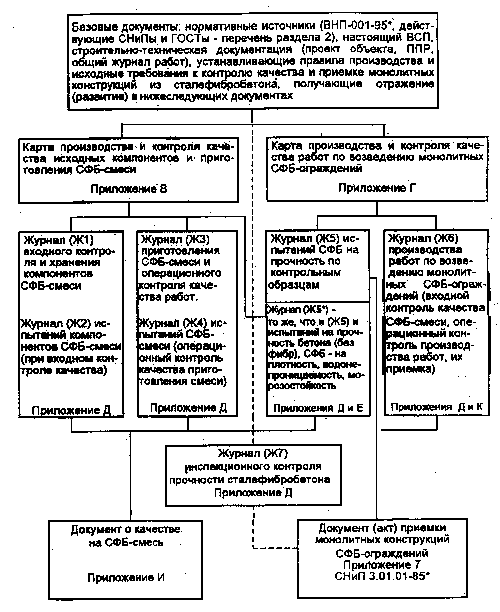
Рисунок 6 - Пример графического представления результатов испытаний для оценки нестабильности
6.2.2.1 Процедура испытаний
Выбирают промежуток времени  (например, интервал между планируемыми калибровками), через который должны быть получены данные для определения нестабильности.
(например, интервал между планируемыми калибровками), через который должны быть получены данные для определения нестабильности.
Используют образцы сравнения, для которых  и
и  (
( и
и 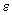 - соответственно, минимальное и максимальное значения
- соответственно, минимальное и максимальное значения 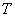 по всем образцам сравнения, применяемым для калибровки;
по всем образцам сравнения, применяемым для калибровки; 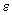 ).
).
В момент времени 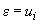 0 регистрируют выходной сигнал
0 регистрируют выходной сигнал  , соответствующий пробе с
, соответствующий пробе с  .
.
Повторяют то же самое для пробы с 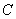 и регистрируют выходной сигнал
и регистрируют выходной сигнал  .
.
Указанную процедуру повторяют через равные интервалы времени 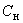 . Общее число измерений
. Общее число измерений 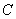 должно быть не менее восьми.
должно быть не менее восьми.
6.2.2.2 Вычисление характеристик
Для 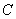 дрейф (угловой коэффициент линии регрессии)
дрейф (угловой коэффициент линии регрессии) 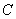 и стандартное отклонение рассеяния
и стандартное отклонение рассеяния 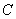 вычисляют по формулам:
вычисляют по формулам:
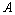 ; (30)
; (30)
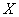 . (31)
. (31)
Аналогично вычисляют параметры 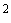 и
и 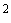 для
для 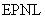 .
.
6.2.2.3 Вычисление дрейфа
Дрейф коэффициентов градуировочной характеристики вычисляют по формулам:
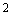 ; (32)
; (32)
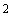 . (33)
. (33)
Отсюда для любого значения 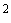 из рассматриваемого диапазона значений получают дрейф оценки характеристики качества воздуха
из рассматриваемого диапазона значений получают дрейф оценки характеристики качества воздуха
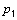 . (34)
. (34)
6.2.2.4 Оценка рассеяния
Стандартные отклонения для 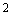 и
и 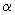 вычисляют при условии, что
вычисляют при условии, что
 ;
;
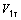 ; (35)
; (35)
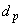 . (36)
. (36)
Наконец, вклад рассеяния в нестабильность оценки характеристики качества воздуха вычисляют по формуле
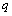 . 37)
. 37)
Если полученное по формуле (37) значение не превышает стандартного отклонения повторяемости (сходимости), то флуктуацию параметров на интервале времени 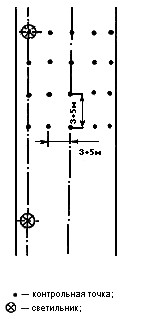 можно считать незначительной.
можно считать незначительной.
6.2.3 Зависимость результатов измерений от влияющих величин
Это испытание предназначено для оценки результатов измерений, выполняемых в условиях применения. Предполагается, что воздействие влияющей величины на результат измерений может быть признано удовлетворительным, если были проведены испытания при предельных значениях влияющих величин (см. рисунок 7).
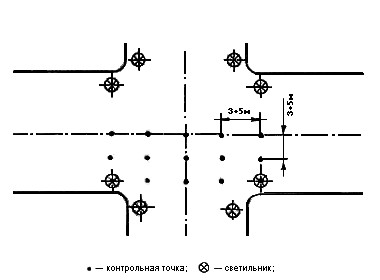
1 - градуировочная характеристика в условиях действия влияющей величины;
2 - градуировочная характеристика в нормальных условиях
Рисунок 7 - Пример изменения линейной градуировочной характеристики под воздействием
влияющей величины (двухуровневый эксперимент)
Влияющие величины разделяют на классы в зависимости от того, известна или неизвестна зависимость влияющей величины на результат измерений. Примерами влияющих величин, характер воздействия которых известен, являются температура и давление, входящие в классическое уравнение состояния газов (до тех пор, пока это классическое уравнение соблюдается). Однако более типичным является случай, когда вид зависимости является более сложным и, как правило, неизвестным. Примером этого может служить влияние температуры через изменение состояния электронных устройств, на которые, кроме того, оказывают влияние изменения напряжения питания и радиопомехи.
6.2.3.1 Вид зависимости известен
Результат измерений 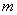 выражают как функцию характеристики качества воздуха и влияющих величин:
выражают как функцию характеристики качества воздуха и влияющих величин:
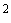 .
.
Коэффициент линейной зависимости 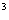 от
от 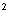 аппроксимируют соответствующей частной производной:
аппроксимируют соответствующей частной производной:
 . (38)
. (38)
6.2.3.2 Вид зависимости неизвестен
В этом случае проводят испытания с использованием образцов сравнения, для которых значение характеристики качества воздуха соответствует нижней и верхней границам исследуемого диапазона 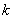 и
и 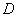 соответственно;
соответственно; 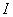 .
.
Чтобы экспериментально определить вид зависимости от влияющей величины, проводят испытания при предельных значениях одной влияющей величины и при значениях остальных влияющих переменных, соответствующих нормальным условиям, следующим образом.
Регистрируют для каждого из значений  разность
разность 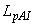 выходных сигналов, полученных для двух предельных значений
выходных сигналов, полученных для двух предельных значений 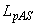 .
.
Зависимость коэффициента линейной зависимости 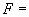 от
от 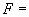 в точках
в точках 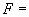 ,
, 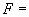 1,
1,  вычисляют по формуле
вычисляют по формуле
 . (39)
. (39)
Зависимость 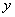 и
и 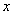 от влияющей величины определяют по формулам:
от влияющей величины определяют по формулам:
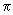 ; (40)
; (40)
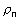 . (41)
. (41)
Для произвольной точки диапазона 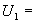 коэффициент линейной зависимости оценки измеряемой величины от влияющей величины
коэффициент линейной зависимости оценки измеряемой величины от влияющей величины 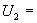 имеет вид
имеет вид
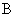 . (42)
. (42)
Согласно ИСО 6879 в первом приближении селективность 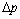 относительно
относительно 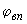 вычисляют по формуле
вычисляют по формуле
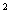 . (43)
. (43)
6.3 Рабочие характеристики измерительной системы
6.3.1 Время установления рабочего режима
Испытания проводят для той характеристики, время стабилизации которой ожидается наибольшим, например предел обнаружения или повторяемость (сходимость).
Исследуют, как время установления рабочего режима зависит от условий работы измерительной системы. Испытания проводят для условий, в которых время установления рабочего режима ожидается наибольшим.
Если измерительная система находилась в рабочем состоянии, то ее возвращают в нерабочее состояние и ждут, пока это состояние стабилизируется. После этого переходят в режим измерений и определяют время, необходимое для достижения исследуемой характеристики диапазона заданных значений.
6.3.2 Период необслуживаемой работы
Исследуют, какая из характеристик, рассмотренных в 6.3.1, наиболее критична к длительности периода необслуживаемой работы. Дальнейшие испытания проводят для этой характеристики.
Исследуют влияние условий работы на возможный период необслуживаемой работы и выбирают наиболее неблагоприятные из них.
Выполняют необходимое техническое обслуживание измерительной системы.
Начинают процесс измерений согласно руководству по эксплуатации в наиболее неблагоприятных рабочих условиях. Регистрируют время, прошедшее до стабилизации характеристик измерительной системы.
Оставляют систему работающей в автономном режиме.
Периодически проверяют значение контролируемой характеристики до тех пор, пока она не выйдет за пределы диапазона допустимых значений.
Регистрируют время, прошедшее от начала работы измерительной системы до момента, когда контролируемая характеристика последний раз была обнаружена в пределах диапазона допустимых значений. Это время принимают за период необслуживаемой работы измерительной системы.
Повторяют испытание несколько раз или для нескольких измерительных систем.
Из всех полученных значений временных интервалов от начала работы до выхода характеристики из допустимых пределов выбирают минимальный, который рассматривают как обобщенное значение периода необслуживаемой работы.
Регистрируют результаты испытаний, включая период и допустимые диапазоны характеристик.
Приложение А
(обязательное)
Двусторонний критерий Граббса для проверки выбросов
В таблице А.1 приведены критические значения для статистики Граббса при уровне значимости 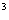 0,05.
0,05.
Таблица А.1
Число повторов |
Критическое значение |
3 |
1,155 |
4 |
1,481 |
5 |
1,715 |
6 |
1,887 |
7 |
2,020 |
8 |
2,126 |
9 |
2,215 |
10 |
2,290 |
11 |
2,355 |
12 |
2,412 |
13 |
2,462 |
14 |
2,507 |
15 |
2,549 |
16 |
2,585 |
17 |
2,620 |
18 |
2,651 |
19 |
2,681 |
20 |
2,709 |
25 |
2,822 |
30 |
2,908 |
40 |
3,036 |
50 |
3,128 |
Приложение В
(обязательное)
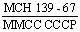 -распределение
-распределение
В таблице В.1 приведены табулированные значения 
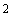 -распределения для одностороннего критерия с уровнем значимости
-распределения для одностороннего критерия с уровнем значимости  0,05.
0,05.
Таблица В.1
|
| |||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 | |
40 |
4,08 |
3,23 |
2,84 |
2,61 |
2,45 |
2,34 |
2,25 |
2,18 |
2,12 |
2,08 |
2,04 |
2,00 |
50 |
4,03 |
3,18 |
2,79 |
2,56 |
2,40 |
2,29 |
2,20 |
2,13 |
2,07 |
2,03 |
1,99 |
1,95 |
60 |
4,00 |
3,15 |
2,76 |
2,53 |
2,37 |
2,25 |
2,17 |
2,10 |
2,04 |
1,99 |
1,95 |
1,92 |
100 |
3,94 |
3,09 |
2,70 |
2,46 |
2,31 |
2,19 |
2,10 |
2,03 |
1,97 |
1,93 |
1,89 |
1,85 |
120 |
3,92 |
3,07 |
2,68 |
2,45 |
2,29 |
2,18 |
2,09 |
2,02 |
1,96 |
1,91 |
1,87 |
1,83 |
|
3,84 |
3,00 |
2,60 |
2,37 |
2,21 |
2,10 |
2,01 |
1,94 |
1,88 |
1,83 |
1,79 |
1,75 |
Для  30 значения
30 значения  могут быть вычислены по формуле
могут быть вычислены по формуле
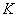 ,
,
где
 .
.
Приложение С
(обязательное)
Распределение Стьюдента (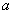 -распределение)
-распределение)
В таблице С.1 приведены табулированные значения односторонних и двусторонних квантилей 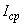 -распределения для уровня
-распределения для уровня  0,05.
0,05.
Таблица С.1
Число степеней свободы |
Односторонний квантиль |
Двусторонний квантиль |
1 |
6,314 |
12,706 |
2 |
2,920 |
4,303 |
3 |
2,353 |
3,182 |
4 |
2,132 |
2,776 |
5 |
2,015 |
2,751 |
6 |
1,943 |
2,447 |
7 |
1,895 |
2,365 |
8 |
1,860 |
2,306 |
9 |
1,833 |
2,262 |
10 |
1,812 |
2,228 |
11 |
1,796 |
2,201 |
12 |
1,782 |
2,179 |
13 |
1,771 |
2,160 |
14 |
1,761 |
2,145 |
15 |
1,753 |
2,131 |
16 |
1,746 |
2,120 |
17 |
1,740 |
2,110 |
18 |
1,734 |
2,101 |
19 |
1,729 |
2,093 |
20 |
1,725 |
2,086 |
30 |
1,697 |
2,042 |
40 |
1,684 |
2,021 |
60 |
1,671 |
2,000 |
|
1,645 |
1,960 |
Значения 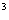 для
для 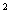 3 могут быть также вычислены по формуле
3 могут быть также вычислены по формуле
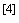 .
.
Значения 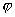 для
для  3 могут быть также вычислены по формуле
3 могут быть также вычислены по формуле
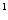 .
.
Приложение D
(справочное)
Сведения о соответствии ссылочных международных (региональных) стандартов
национальным стандартам Российской Федерации
Таблица D.1
Обозначение ссылочного международного стандарта |
Обозначение и наименование соответствующего национального или межгосударственного стандарта |
ИСО 3534-1:1993 |
ГОСТ Р 50779.10-2000 Статистические методы. Вероятность и основы статистики. Термины и определения |
ИСО 5725-2:1994 |
ГОСТ Р ИСО 5725-2-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений |
ИСО 6879:1995 |
Библиография
[1] |
Grubbs, F.E. and Beck, G. Extension of sample sizes and percentages points for significance tests of outlying observations. Technometrics, 14,1972, pp.847-854 |
[2] |
Garden, J.S., Mitchell, D.G. and Mills, W.N. Non-constant variance regression techniques for calibration-curve-based analysis. Anal. Chem., 52, 1980, pp.2310-2315 |
[3] |
Green, J.R. and Margerison, D. Statistical Treatment of Experimental Data. Elseivier, Amsterdam, 1978 |
[4] |
Draper, N.R. and Smith, H. Applied Regression Analysis. Wiley, New York, 1966 |
[5] |
Natrella, M.G. Exerimental statistics. In: NBS Handbook 91, 1966 |
[6] |
Dixon, W.J. and Massey, F.J. Introduction to Statistical Analysis. McGraw-Hill, New York, 1969 |

 Уроженка Краснодара Владлена Бобровникова победила рак и попала в шоу...
Уроженка Краснодара Владлена Бобровникова победила рак и попала в шоу...  Создайте свой интернет-магазин на новой платформе ReadyScript
Создайте свой интернет-магазин на новой платформе ReadyScript  Хостинг, домены, VPS/VDS, размещение серверов
Хостинг, домены, VPS/VDS, размещение серверов