главная сделать стартовой в избранное
почта Моя жизнь помощь регистрация вход
Краснодар:
 погода
февраля
17
понедельник,
Вход в систему
Логин:
Пароль: забыли?

Использовать мою учётную запись:
Вконтакте Mail.ru Одноклассники

Курсы

  • USD ЦБ 03.12 30.8099 -0.0387
  • EUR ЦБ 03.12 41.4824 -0.0244

Индексы

  • DJIA 03.12 12019.4 -0.01
  • NASD 03.12 2626.93 0.03
  • RTS 03.12 1545.57 -0.07

  отправить на печать

     
     РД 50-25645.325-89

Группа Т27

РУКОВОДЯЩИЙ НОРМАТИВНЫЙ ДОКУМЕНТ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Спутники Земли искусственные. Основные системы координат
для баллистического обеспечения полетов и методика расчета звездного времени

ОКСТУ 0003

Дата введения 1990-07-01

ИНФОРМАЦИОННЫЕ ДАННЫЕ

     1. ИСПОЛНИТЕЛИ
     
     Т.А.Амелина, В.А.Анисимов, И.И.Волков, А.А.Горлашкин, И.Ю.Корогодин, И.М.Кузенкова, А.И.Назаренко, Н.А.Пегахин, В.С.Саморуков, Т.В.Скопинская, Г.В.Степанов, Л.В.Ческидова, В.С.Юрасов
     
     2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта СССР от 30.05.89 N 1375
     
     3. Срок проверки - 1995 г.
     
     4. ВВЕДЕН ВПЕРВЫЕ
     
     5. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ:
     

Обозначение НТД, на который дана ссылка

Номер пункта, подпункта, перечисления, приложения

ГОСТ 15855-77*

1 (приложение 1)

________________
     * На территории Российской Федерации действует ГОСТ 8.567-99. Здесь и далее по тексту. - Примечание изготовителя базы данных.
     
     
     Настоящие методические указания (МУ) устанавливают основные системы координат для баллистического обеспечения полетов искусственных спутников Земли (ИСЗ) и методику расчета звездного времени, используемого для преобразования координат из одной системы в другую.
     
     Методические указания предназначены для использования в расчетах по определению орбит ИСЗ и приведения полученных результатов к одинаковым условиям.
     
     Основные термины, используемые в настоящих методических указаниях, и пояснения к ним приведены в приложении 1.
     
     В приложении 2 приведены матрицы перехода, обеспечивающие взаимосвязь основных систем координат.
     
     В приложении 3 приведены описание и тексты программ расчета матриц перехода и звездного времени на языке ФОРТРАН для ЭВМ БЭСМ-6.
     
     В приложении 4 приведены примеры расчета матриц прецессии, нутации и звездного времени.
     
     

1. ОСНОВНЫЕ СИСТЕМЫ КООРДИНАТ

     1.1. В качестве основных систем координат в методических указаниях установлены следующие системы:
     
     фундаментальная инерциальная система координат эпохи ;
     
     инерциальная система координат эпохи ;
     
     динамическая система координат эпохи ;
     
     гринвичская система координат.
     
     1.2. В качестве эпохи  принята эпоха фундаментального звездного каталога FK5: 2000 г., январь 1, 12 (январь 1,5). Эпохе , обозначаемой 2000.0, соответствует юлианская дата 2451545.0.
     
     Эпоха  соответствует моменту времени, к которому отнесены преобразуемые значения координат.
     
     1.3. Фундаментальная инерциальная система координат эпохи  - прямоугольная система координат , имеющая начало в центре масс  Земли.
     
     Ось  направлена в среднюю точку весеннего равноденствия эпохи .
     
     Ось  направлена по нормали к плоскости среднего экватора эпохи  к Северному полюсу мира.
     
     Ось  дополняет систему  до правой.
     
     1.4. Инерциальная система координат эпохи  - прямоугольная система координат , имеющая начало в центре масс  Земли.
     
     Ось  направлена в истинную точку весеннего равноденствия эпохи .
     
     Ось  направлена по мгновенной оси вращения Земли в эпоху  в сторону Северного полюса мира.
     
     Ось  дополняет систему  до правой.
     
     1.5. Динамическая система координат эпохи  - прямоугольная система координат , имеющая начало в центре масс  Земли.
     Ось  лежит в плоскости истинного экватора эпохи  и направлена в точку , которая отклонена от истинной точки весеннего равноденствия на часовой угол, равный сумме значений прецессии в прямом восхождении за интервал времени от эпохи  до эпохи  и нутации в прямом восхождении в эпоху .
     
     Ось  направлена по мгновенной оси вращения Земли в эпоху  в сторону Северного полюса.
     
     Ось  дополняет систему  до правой.
     
     1.6. Гринвичская система координат - прямоугольная система координат , имеющая начало в центре масс  Земли, вращающаяся вместе с Землей.
     
     Ось  направлена к Международному условному началу.
     
     Ось  лежит в плоскости среднего гринвичского меридиана и определяет положение нуль-пункта принятой системы счета долгот.
     
     Ось  дополняет систему  до правой.
     
     

2. МЕТОДИКА РАСЧЕТА ЗВЕЗДНОГО ВРЕМЕНИ

     2.1. Звездное время на меридиане места наблюдения измеряют часовым углом точки весеннего равноденствия  относительно меридиана наблюдателя.
     
     Гринвичское истинное (среднее) звездное время  измеряют часовым углом истинной (средней) точки весеннего равноденствия  относительно гринвичского меридиана.
     
     Гринвичское модифицированное звездное время  измеряют часовым углом точки  относительно гринвичского меридиана.
     
     Аргументом для вычисления звездного времени является всемирное время .
     
     2.2. Гринвичское среднее звездное время  в эпоху  вычисляют по формуле
     

                   (1)

     
где  - час;
         
       - минута;
         
       - секунда;
     
      - интервал времени от эпохи  до эпохи  в средних солнечных сутках, вычисляемый по формуле
     

;                                              (2)

     
    
      - всемирное время  рассматриваемой даты, выраженное в долях суток;
    
      - интервал времени от эпохи  до эпохи  в юлианских столетиях по  средних солнечных суток, вычисляемый по формуле
     

.                                                        (3)

     
     2.3. Гринвичское истинное звездное время  вычисляют по формуле
     

,                                                    (4)

     
где  - нутация в прямом восхождении в эпоху .
     
     2.4. Гринвичское модифицированное звездное время  в эпоху  вычисляют по формуле
     

              (5)

     
     2.5. Для расчета звездного времени на определенную эпоху, выраженную в системе всемирного координированного времени , необходимо предварительно учесть поправку  за переход от  к :
     

,                                                 (6)

     
а затем по полученному аргументу вычислить звездное время.
     
     Приближенные значения поправок  передаются радиосигналами посредством специального кода. Уточненные значения поправок приводят в бюллетене "Всемирное время и координаты полюса", издаваемом Государственной комиссией единого времени и эталонных частот СССР.
     
     

3. ПРЕОБРАЗОВАНИЕ КООРДИНАТ

     3.1. Преобразования, связанные с переходом от фундаментальной инерциальной системы координат эпохи  к инерциальной системе координат эпохи  и обратно, осуществляют по формулам:
     

,                                                     (7)

     
,                                                  (8)

     
где , ,  - координаты, определенные в инерциальной системе координат эпохи ;
                  
     , ,  - координаты, определенные в фундаментальной инерциальной системе координат эпохи ;
           
      - матрица нутации в эпоху ;
          
       - матрица прецессии, определяющая переход от среднего экватора и точки  (эпохи ) к среднему экватору и точке   (эпохи ).
     
     Индекс  означает транспонирование матрицы.
     
     Формулы для вычисления матриц  и  приведены в приложении 2.
     
     3.2. Преобразования, связанные с переходом от инерциальной системы координат эпохи  к гринвичской системе координат и обратно, осуществляют по формулам:
     

,                                                  (9)

     
,                                               (10)

     
где , ,  - координаты, определенные в гринвичской системе координат;
         
       - матрица, учитывающая смещение положения мгновенного полюса Земли в эпоху  относительно Международного условного начала;
          
       - матрица учета суточного вращения Земли.
     
     Формулы для вычисления матриц  и  приведены в приложении 2.
     
     3.3. Преобразования, связанные с переходом от фундаментальной инерциальной системы координат эпохи  к динамической системе координат эпохи  и обратно, осуществляют по формулам:
     

,                                               (11)


,                                            (12)

     
где , ,  - координаты, определенные в динамической системе координат;
          
       - матрица учета прецессии и нутации в прямом восхождении.
     
     Формулы для вычисления матрицы  приведены в приложении 2.
     
     3.4. Преобразования, связанные с переходом от динамической системы координат эпохи  к инерциальной системе координат эпохи  и обратно, осуществляют по формулам:
     

,                                                     (13)


.                                                    (14)

     
     3.5. Преобразования, связанные с переходом от динамической системы координат эпохи  к гринвичской системе координат и обратно, осуществляют по формулам:
     

,                                               (15)


,                                               (16)

     
где  - матрица поворота динамической системы координат эпохи  вокруг оси  на угол, равный гринвичскому модифицированному звездному времени.
     
     Формулы для вычисления матрицы  приведены в приложении 2.
     
     3.6. Преобразования, связанные с переходом от фундаментальной инерциальной системы координат эпохи  к гринвичской системе координат и обратно, осуществляют по формулам:
     

,                                           (17)


.                                       (18)


или

,                                     (19)
    
     
     .                                 (20)



ПРИЛОЖЕНИЕ 1
Справочное

ОСНОВНЫЕ ТЕРМИНЫ,
ИСПОЛЬЗУЕМЫЕ В МЕТОДИЧЕСКИХ УКАЗАНИЯХ, И ПОЯСНЕНИЯ К НИМ

Термин

Пояснение*

1. Эпоха

Численное выражение момента событий, указанное в какой-либо шкале времени

2. Всемирное время  

Среднее солнечное время среднего гринвичского меридиана, в положении которого учтено влияние движения полюсов Земли

3. Всемирное координированное время

Атомное время, корректируемое при необходимости на целую секунду в ту или иную сторону 31 декабря и (или) 30 июня таким образом, чтобы разница между ним и всемирным временем  не превышала 0,9 с:



4. Истинный экватор

Плоскость, проходящая через центр масс Земли перпендикулярно к мгновенной оси ее вращения.

Примечание. Истинный экватор Земли определяется с учетом прецессии и нутации

5. Средний экватор

Плоскость, проходящая через центр масс Земли перпендикулярно к средней оси ее вращения.

Примечание. Средний экватор Земли определяется с учетом только прецессии

6. Истинная (средняя) точка весеннего равноденствия



Точка пересечения эклиптики и истинного (среднего) экватора, соответствующая переходу Солнца из южного полушария небесной сферы в северное

7. Прецессия

Совокупность векового движения оси вращения Земли относительно оси, проходящей через полюс эклиптики, под влиянием притяжения Луны и Солнца (лунно-солнечная прецессия) и вращения плоскости эклиптики под влиянием притяжения планет (прецессия от планет)

8. Нутация

Совокупность периодических движений оси вращения Земли относительно системы координат, неподвижной в пространстве, под влиянием притяжения Луны и Солнца

9. Юлианская дата

Число средних солнечных суток, отсчитанных от гринвичского полудня 1 января 4713 г. до н. э. до эпохи .

Примечание. Юлианские даты, соответствующие 12 0-го дня каждого месяца приводятся в таблице "Юлианский период" "Астрономического ежегодника СССР"

10. Международное условное начало

Среднее положение Северного полюса Земли 1900-1905 гг., определенное номинальными значениями широт, принятыми в качестве абсолютных постоянных пяти широтных обсерваторий Международной службы движения полюсов

________________
     * См. также ГОСТ 15855-77
     
     

ПРИЛОЖЕНИЕ 2
Справочное

МАТРИЦЫ ПЕРЕХОДА,
ОБЕСПЕЧИВАЮЩИЕ ВЗАИМОСВЯЗЬ ОСНОВНЫХ СИСТЕМ КООРДИНАТ

     1. Матрица прецессии имеет вид
     

,                                                     (21)

     
где ;
     
     ;
     
     ;
     
     ;
     
     ;
     
     ;
     
     ;
     
     ;
     
     .
     
     Прецессионные параметры , ,  вычисляют по формулам:

     
    
     
     

     
     Прецессионные параметры такого вида применимы только при преобразовании от фундаментальной эпохи 2000,0 к эпохе  и наоборот.
     
     2. Матрица нутации  имеет вид
     

,                                                  (22)

     
где ;
     
     ;
     
     ;
     
     ;
     
     ;
     
     ;
     
     ;
     
     ;
     
     ;
     
      - нутация в долготе:
     
      - истинный наклон эклиптики к экватору, вычисляемый по формуле
     

;

     
      - средний наклон эклиптики к экватору, вычисляемый по формуле
     

     
      - нутация в наклоне.
     
     Нутацию в долготе  и нутацию в наклоне  определяют разложениями:
     

,

,

     
где , , ,  - коэффициенты, входящие в амплитуду каждого члена нутации  и ;
          
     , , , ,  - коэффициенты при фундаментальных аргументах , , , ,  теории движения Луны;
         
      - средняя аномалия Луны;
          
      - средняя аномалия Солнца;
        
      - средний аргумент широты Луны;
           
      - разность средних долгот Луны и Солнца;
        
      - средняя долгота восходящего узла орбиты Луны на эклиптике.
     
     Разложения фундаментальных аргументов имеют вид:
     

     
     Значения коэффициентов , , , , , , , , , (1, 2, 3, ..., 106) разложений нутации в долготе и нутации в наклоне приведены в "Астрономическом ежегоднике СССР" (с 1986 г.).
     
     С точностью до членов порядка  (или ) значения нутации в долготе  и нутации в наклоне  вычисляют по формулам:
     

            (23)

     
             (24)

     
     Матрица нутации с точностью до малых членов порядка  имеет вид
     

.                           (25)

     
     3. Матрица поворота  имеет вид
     

,                                            (26)

     
где  - значение гринвичского истинного звездного времени в эпоху .
     
     4. Матрица поворота  имеет вид
     

,                                              (27)

     
где  - значение гринвичского модифицированного звездного времени в эпоху .
     
     5. Матрица  имеет вид
     

,                                               (28)

     
где ,  - координаты мгновенного полюса Земли, выраженные в радианах.
     
     Положение мгновенного полюса в эпоху  определяют в системе прямоугольных координат , начало которой  совпадает с Международным условным началом.
     
     Ось  направлена по касательной к гринвичскому меридиану.
     
     Ось  направлена по касательной к меридиану, отстоящему от гринвичского меридиана на угол 90° к западу.
     
     Значения координат мгновенного полюса ,  в угловых секундах выбирают из бюллетеня "Всемирное время и координаты полюса".
     
     6. Матрица учета прецессии и нутации в прямом восхождении имеет вид
     

,                                    (29)

     
где  - прецессия в прямом восхождении за интервал времени от эпохи  до эпохи .
     
     Значение  соответственно в угловых секундах и радианах вычисляют по формуле
     

     
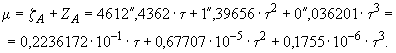
     7. Значение нутации в прямом восхождении  вычисляют по формуле
     

.                                                     (30)


ПРИЛОЖЕНИЕ 3
Справочное

ОПИСАНИЕ И ТЕКСТЫ ПРОГРАММ РАСЧЕТА МАТРИЦ ПЕРЕХОДА
И ЗВЕЗДНОГО ВРЕМЕНИ НА ЯЗЫКЕ ФОРТРАН ДЛЯ ЭВМ БЭСМ-6

     1. Подпрограмма JULE (NDMG, Т, JD, DJD, DM, D) предназначен для расчета юлианской даты с 1900 по 2099 гг., всемирного времени  рассматриваемой даты в долях суток и интервала времени от эпохи 2000.0 до эпохи Т.
     

Вход: NDMG -

дата, месяц, год, записанные в виде целого числа;

например, 6 мая 1988 г. соответствует запись 06051988;

Т -

всемирное время  рассматриваемой даты в часах, минутах, секундах;

например, 13 ч 35 мин 12,79 с будет соответствовать 133512,79.

Выход: JD -

целая часть юлианской даты;

DJD -

дробная часть юлианской даты в долях суток;

   

     D -

интервал времени от эпохи 2000.0 до эпохи Т в средних солнечных сутках;

DM -

всемирное время  рассматриваемой даты, выраженное в долях суток.

     
     2. Подпрограмма SCP (D, DM, SC) предназначена для расчета гринвичского среднего звездного времени.

     

Вход: D -

интервал времени от эпохи 2000.0 до эпохи Т в средних солнечных сутках;

DM -

всемирное время  рассматриваемой даты, выраженное в долях суток.

Выход: SC -

гринвичское среднее звездное время, выраженное в радианах.

     
     3. Подпрограмма SMOD (D, DM, SM) предназначена для расчета гринвичского модифицированного звездного времени.
     

Вход: D -

интервал времени от эпохи 2000.0 до эпохи Т в средних солнечных сутках;

DM -

всемирное время  рассматриваемой даты, выраженное в долях суток.

Выход: SM -

гринвичское модифицированное звездное время, выраженное в радианах.

     
     4. Подпрограмма SICT (D, DM, NP1, SI) предназначена для расчета гринвичского истинного звездного времени.
     

Вход: D -

интервал времени от эпохи 2000.0 до эпохи Т в средних солнечных сутках;

DM -

всемирное время  рассматриваемой даты, выраженное в долях суток;

NP1 -

признак выбора формул для расчета нутации в долготе и наклоне, равный 0 или 1:

NP1=0

- значения нутации в долготе и наклоне вычисляются по полным формулам;

NP1=1

- значения нутации в долготе и наклоне определяются с точностью до членов порядка 0".1 (или 1.Е-6).

Выход: SI -

гринвичское истинное звездное время, выраженное в радианах.

     
     5. Подпрограмма НУТАС (D, NP1, HPCI, HEPC, EPC, EPC0) предназначена для расчета нутации в долготе и нутации в наклоне, а также расчета истинного и среднего наклона эклиптики к экватору.
     

Вход: D -

интервал времени от эпохи 2000.0 до эпохи Т в средних солнечных сутках;

NP1 -

признак выбора формул для расчета нутации в долготе и наклоне, равный 0 или 1:

NP1=0

- значения нутации в долготе и наклоне вычисляются по полным формулам;

NP1=1

- значения нутации в долготе и наклоне определяются с точностью до членов порядка 0".1 (или 1.Е-6).

Выход: HPCI -

нутация в долготе, выраженная в радианах;

HEPC -

нутация в наклоне, выраженная в радианах;

EPC -

истинный наклон эклиптики к экватору, выраженный в радианах;

EPC0 -

средний наклон эклиптики к экватору, выраженный в радианах.

     
     6. Подпрограмма НУТМАТ (D, NP1, NP2, НМ) предназначена для расчета матрицы нутации.
     

Вход: D -

интервал времени от эпохи 2000.0 до эпохи Т в средних солнечных сутках;

NP1 -

признак выбора формул для расчета нутации в долготе и наклоне, равный 0 или 1:

NP1=0

- значения нутации в долготе и наклоне вычисляются по полным формулам;

NP1=1

- значения нутации в долготе и наклоне определяются с точностью до членов порядка 0".1 (или 1.Е-6).

NP2 -

признак выбора формул для расчета матрицы нутации, равный 0 или 1:

NP2=0

- матрица нутации вычисляется по точным формулам;

NP2=1

- матрица нутации вычисляется по упрощенным формулам.

Выход: НМ -

матрица нутации.

     
     7. Подпрограмма PREMAT (D, PM) предназначена для расчета матрицы прецессии.
     

Вход: D -

интервал времени от эпохи 2000.0 до эпохи Т в средних солнечных сутках;

Выход: РМ -

матрица прецессии.

     
     8. Подпрограмма RMUMAT (D, NP1, RM) предназначена для расчета матрицы учета прецессии и нутации в прямом восхождении.
     

Вход: D -

интервал времени от эпохи 2000.0 до эпохи Т в средних солнечных сутках;

NP1 -

признак выбора формул для расчета нутации в долготе и наклоне, равный 0 или 1:

NP1=0

- значения нутации в долготе и наклоне вычисляются по полным формулам;

NP1=1

- значения нутации в долготе и наклоне определяются с точностью до членов порядка 0".1 (или 1.Е-6).

Выход: RM -

матрица учета прецессии и нутации в прямом восхождении.

     
     9. Тексты программ
     

SUBROUTINE JULЕ (NDMG, Т, JD, DJD, DM, D)     
NG=NDMG-(NDMG/10000)*10000     
N=NDMG/1000000     
NM=(NDMG-NG-N*1000000)/10000     
JT=Т/10000     
JM=T/100.-JT*100     
JC-T/100.     
JC=JC*100     
C=T-JC     
DM=JT/24.+JM/1440.+C/86400.     
K=NM-1     
IF (K.EQ.0) GO TO 1     
DO 1 I=1, K     
GC TO (2, 3, 2, 4, 2, 4, 2, 2, 4, 2, 4), I

2

N=N+31     
GO TO 1

3

N=N+28     
GO TO 1

4

N=N+30

1

CONTINUE
L=NG-1900
KK=L/4
J=KK*4
IF (NM.GT.2.AND.J.EQ.L.AND.L.NE.0) N=N+1
J=(L-1)/4
JD=N+J+L*365+2415019
IF (DM.LT,0.5) GO TO 10
DJD=DM-0.5
JD=JD+1
GO TO 11

10

DJD=DM+0.5

11

CONTINUE
D=JD+DJD-2451545.0
RETURN
END

C

********** ********** ********** ********** ********** *****
SUBROUTINE SCP (D, DM, SC)
ТАУ=D/36525.
SC=1.7533685592+1.72027918051*1.E-2*D+6.28318530718*DM

*+6.

77071394*1.Е-6*ТАУ*ТАУ-4.50876723*1.Е-10*ТАУ*ТАУ*ТАУ
KSC=SC/6.28318530718
IF (KSC.LT.0) KSC=KSC-1
SC=SC-KSC*6.28318530718
RETURN
END

C

********** ********** ********** ********** ********** *****
SUBROUTINE SMOD (D, DM, SM)
TAУ=D/36525.
SM=1.7533685592+0.01720217957*D+6.28318530718*DM

*-1.

75958*1.Е-7*ТАУ*ТАУ*ТАУ
KSM=SM/6.28318530718
IF (KSM.LT.0) KSM=KSM-1
SM=SM-KSM*6.28318530718
RETURN
END

C

********** ********** ********** ********** ********** *****
SUBROUTINE SICT (D, DM, NP1, Sl)
CALL HYTAC (D, NP1, HP, HE, Е, E0)
HALFA=HP*COS (Е)
CALL SCP (D, DM, SC)
SI=SC+HALFA
RETURN
END

C

********** ********** ********** ********** ********** *****
SUBROUTINE НУТАС (D, NP1, HPCI, HEPC, EPC, EPC0)
DIMENSION KL (106), KL1 (106), KF (106), KD (106), KОМ (106)
DIMENSION APCI (106), BPCI (106), AEPC (106), BEPC (106)
DATA ((KL (I), I=1, 22)=0, 0, -2, 2, -2, 1, 0, 2, 0, 0, 0, 0, 0, 2,
*0, 0, 0, 0, 0, -2, 0, 2)
DATA ((KL (I), I=23, 44)=0, 1, 2, 0, 0, 0, -1, 0, 0, 1, 0, 1, 1, -1,
*0, 1, -1, -1, 1, 0, 2, 1)
DATA ((KL (I), I=45, 66)=2, 0, -1, -1, 1, -1, 1, 0, 0, 1, 1, 2, 0, 0, 1,
*0, 1, 2, 0, 1, 0, 1)
DATA ((KL (I), I=67, 88)=1, 1, -1, -2, 3, 0, 1, -1, 2, 1, 3, 0, -1, 1,
*-2, -1, 2, 1, 1, -2, -1, 1)
DATA ((KL (I), I=89, 106)=2, 2, 1, 0, 3, 1, 0, -1, 0, 0, 0, 1, 0, 1, 1,
*2, 0, 0)
DATA ((KL1 (I), I=1, 22)=0, 0, 0, 0, 0, -1, -2, 0, 0, 1, 1, -1, 0, 0, 0,
*2, 1, 2, -1, 0, -1, 0)
DATA ((KL1 (I), I=23,44)=1, 0, 1, 0, 1, 1, 0, 1,
*0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
DATA ((KL1 (I), I=45, 66)=0, 0, 0, 0, 0, 0, 1, 1, -1,
*0, 0, 0, 0, 0, 0, 0, -1, 0, 1, 0, 0, 1)
DATA ((KL1 (I), I=67,88)=0, -1, -1, 0, 0, -1, 1, 0, 0, 0, 0, 0,
*0, 0, 0, 0, 0, 1, 0, 0, 0, -1)
DATA ((KL1 (I), I=89,106)=0, 0, 0, 0, 0, 0, 1, -1, 0, 0, 1, 0,
*-1, 1, 0, 0, 0, 1)
DATA ((KF (I), I=1, 22)=0, 0, 2, -2, 2, 0, 2, -2, 2, 0, 2, 2, 2,
*0, 2, 0, 0, 2, 0, 0, 2, 0)
DATA ((KF (I), I=23, 44)=2, 0, 0, -2, -2, 0, 0, 2, 2, 0, 2, 2, 0, 2,
*0, 0, 0, 2, 2, 2, 0, 2)
DATA ((KF (I), I=45, 66)=2, 2, 2, 0, 0, 2, 0, 2, 2, 2, 0, 2, 0,
*2, 2, 0, 0, 2, 0, -2, 0, 0)
DATA ((KF (I), I=67, 88)=2, 2, 2, 0, 2, 2, 2, 2, 0, 0, 0,
*2, 0, 0, 2, 2, 0, 2, 2, 2, 4, 0)
DATA ((KF (I), I=89, 106)=2, 2, 0, 4, 2, 2, 2, 0, -2, 2, 0,
*-2, 2, 0, -2, 0, 2, 0)
DATA ((KD (I), I=1, 22)=0, 0, 0, 0, 0, -1, -2, 0, -2, 0,
*-2, -2, -2, -2, -2, 0, 0, -2, 0, 2, -2, -2)
DATA ((KD (I), I=23, 44)=-2, -1, -2, 2, 2, 0, 1, -2, 0, 0, 0, 0,
*-2, 0, 2, 0, 0, 2, 0, 2, 0, -2)
DATA ((KD (I), I=45, 66)=0, 0, 0, 2, -2, 2, -2, 0, 0, 2, 2, -2, 2, 2, -2,
*-2, 0, 0, -2, 0, 1, 0)
DATA ((KD (I), I=67, 88)=0, 0, 2, 0, 0, 2, 0, -2, 0, 0, 0, 1, 0,
*-4, 2, 4, -4, -2, 2, 4, 0, -2)
DATA ((KD (I), I=89, 106)=-2, 2, 2, -2, -2, -2, 0, 2, 0, -1, 2,
*-2, 0, -2, 2, 2, 4, 1)
DATA ((KОМ (I), I=1, 22)=1, 2, 1, 0, 2, 0, 1, 1, 2, 0, 2, 2, 1,
*0, 0, 0, 1, 2, 1, 1, 1, 1)
DATA ((KОМ (I), I=23,44)=1, 0, 0, 1, 0, 2, 1, 0, 2, 0, 1, 2, 0, 2, 0,
*1, 1, 2, 1, 2, 0, 2)
DATA ((KOM (I), I=45, 66)=2, 0, 1, 1, 1, 1, 0, 2, 2, 2, 0, 2, 1, 1, 1, 1,
*0, 1, 0, 0, 0, 0)
DATA ((KОМ (I), I=67, 88)=0, 2, 2, 1, 2, 2, 2, 1, 1, 2, 0, 2, 2, 0, 2, 2,
*0, 2, 1, 2, 2, 0)
DATA ((KОМ (I), I=89, 106)=1, 2, 1, 2, 2, 0, 1, 1, 1, 2, 0, 0, 1, 1, 0,
*0, 2, 0)
DATA ((APCI (I), I=1,22)=-171996., 2062., 46., 11., -3.,
*-2., 1., -13187., 1426., -517., 217., 129., 48., -22., 17., -15.,
*-16., -12., -6., -5., 4.)
DATA ((APCI (I), I=23, 44)=4., -4., 1., 1., -1., 1., 1., -1.,
*-2274., 712., -386., -301., -158., 123., 63., 63., -58., -59.,
*-51., -38., 29., 29.)
DATA ((APCI (I), I=45, 66)=-31., 26., 21., 16., -13., -10., -7.,
*7., -7., -8., 6., 6., -6., -7., 6., -5., 5., -5., -4., 4., -4., -3.)
DATA ((APCI (I), I=67, 88)=3., -3., -3., -2., -3., -3., 2., -2.,
*2., -2., 2., 2., 1., -1., 1., -2., -1., 1., -1., -1., 1., 1.)
DATA ((APCI (I), I=89, 106)=1., -1., -1., 1., 1., -1., 1., 1., -1.,
*-1., -1., -1., -1., -1., -1., 1., -1., 1.)
DATA ((BPCI (I), I=1, 22)=-174.2, 0.2, 0.0, 0.0, 0.0, 0.0, 0.0,
*0.0, -1.6, -3.4, 1.2, -0.5, 0.1, 0.0, 0.0, -0.1, 0.0, 0.1, 0.0,
*0.0, 0.0, 0.0)
DATA ((BPCI (I), I=23, 44)=0., 0., 0., 0., 0., 0., 0., 0., -0.2,
*0.1, -0.4, 0.0, 0.0, 0.0, 0.0, 0.1, -0.1, 0.9, 0.0, 0.0, 0.0, 0.0)
DATA ((BPCI (I), I=45,66)=0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
*0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
DATA ((BPCI (I), I=67,88)=0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
DATA ((BPCI (I), I=89,106)=0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
*0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
DATA ((AEPC (I), I=1, 22)=92025., -895., -24., 0., 1., 0., 1., 0.,
*5736., 54., 224., -95., -70., 1., 0., 0., 9., 7., 6., 3., 3., -2.)
DATA ((AEPC (I), I=23, 44)=-2., 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
*977., -7., 200., 129., -1., -53., -2., -33., 32., 26., 27., 16.,
*-1., -12.)
DATA ((AEPC (I), I=45, 66)=13., -1., -10., -8., 7., 5., 0., -3.,
*3., 3., 0., -3., 3., 3., -3., 3., 0., 3., 0.0, 0.0, 0.0, 0.0)
DATA ((AEPC (I), I=67, 88)=0., 1., 1., 1., 1., 1., -1., 1., -1., 1.,
*0., -1., -1., 0., -1., 1., 0., -1., 1., 1., 0., 0.)
DATA ((AEPC (I), I=89, 106)=-1., 0., 0., 0., 0.0, 0.0, 0.0, 0.0, 0.0,
*0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
DATA ((BEPC (I), I=1, 22)=8.9, 0.5, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
*-3.1, -0.1, -0.6, 0.3, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
*0.0)
DATA ((BEPC (I), I=23, 44)=0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
*-0.5, 0.0, 0.0, -0.1, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
*0.0)
DATA ((BEPC (I), I=45, 66)=0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
*0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
DATA ((BEPC (I), I=67,88)=0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
*0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0,0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0,0)
DATA ((BEPC (I), I=89, 106)=0.0, 0.0, 0.0, 0.0,
*0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0,0)
TAУ=D/36525.
ТАУ2=ТАУ*ТАУ
ТАУ3=ТАУ2*ТАУ
EPCO=0.4090928042-0.2269655*1.E-3*TAУ-0.29*1.E-8*TAУ2+
*0.88*1.Е-8*ТАУ3
FL1=6.24003594+628.30195602*TAУ-2.7974*1.Е-6*ТАУ2-5.82*
*1.E-8*ТАУ3
F=1.62790193+8433.46615831*TAУ-6.42717*1.E-5*TAУ2+5.33*
*1.E-8*ТАУ3
D1=5.19846951+7771.37714617*ТАУ-3.34085*.1.Е-5*ТАУ2+9.21*
*1.Е-8*ТAУ3
ОМ=2.182438624-33.757045936*ТАУ+3.61429*1.E-5*ТАУ2+3.88*
*1.Е-8*ТАУ3
IF (NP1.EQ.1) GO TO 3
FL=2,355548393+8328.69142288*ТАУ+1.517952*1.Е-4*ТАУ2+
*3.103*1.Е-7*ТАУ3
HPCI=0
HEPC=0
DO 2 I=1,106
APG=KL (I)*FL+KL1 (I)*FL1+KF (I) *F+KD (I) *D1+KOM (I)*OM
HPCI=HPCI+(APCI (I)+BPCI (I)*TAУ)*SIN (APG)
HEPC=HEPC+(AEPC (I)+BEPC (I) *TAУ*COS (APG)

2

CONTINUE
HPCI=HPCI*4.848136811*1.E-10
HEPC=HEPC*4.848136811*1.E-10
GO TO 4

3

SOM=SIN (OM)
СОМ=COS (OM)
HPCI=-0,83386*1.E-4*SOM+1.9994*1.E-6*COM*SOM-0,63932*
*1.E-5*SIN (2* (F-D1+OM))+0.6913*1.E-6*SIN (FL1)-0,11024*
*1.E-5*SIN (2* (F+OM))
HEPC=0.44615*1.E-4*COM+0.27809*1.E-5*COS (2*(F-D1+OM))
*+0.474*1.E-6*COS (2*(F+OM))

4

CONTINUE
EPC=EPCO+HEPC
RETURN
END

C

********** ********** ********** ********** ********** ******
SUBROUTINE НУТМАТ (D, NP1, NP2, HM)
DIMENSION HM (3, 3)
CALL НУТАС (D, NP1, HP, HE, E, E0)
SE=SIN (E)
CЭ*=COS (E)

________________
     * Текст соответствует оригиналу. - Примечание изготовителя базы данных.     
     

IF (NP2.EQ.1) GO TO 1
SE0=SIN (E0)
CE0=COS (E0)
SHPCI=SIN (HP)
СНПС=СOS (HP)
HM (1, 1)=CHPCI
HM (1, 2)=-SНРСI*СЕ0
HM (1, 3)=-SHPCI*SE0
HM (2, 1)=SHPCI*CE
HM (2, 2)=CHPCI*CE*CE0+SE*SE0
HM (2, 3)=CHPCI*CE*SE0-SE*CE0
HM (3, 1)=SHPCI*SE
HM (3, 2)=CHPCI*SE*CE0-CE*SE0
HM (3, 3)=СНРСI*SЕ*SЕ0+СЕ*CЕ0
GO TO 2

1

HM (1, 1)=1
HM (1, 2)=-HP*CE
HM (1, 3)=-HP*SE
HM (2, 1)=HP*CE
HM (2, 2)=1
HM (2, 3)=-HE
HM (3, 1)=HP*SE
HM (3, 2)=HE
HM (3, 3)=1

2

CONTINUE
RETURN
END
SUBROUTINE PREMAT (D, PM)
DIMENSION PM (3,3)
TAУ=D/36525.
ТАУ2=ТАУ*ТАУ
ТАУ3=ТАУ2*ТАУ
DZETA=0.111808609*1.E-1*ТАУ+0.146356*1.Е-5*ТАУ2+0.872*
*1.Е-7*ТАУ3
Z=0,0111808609*TAУ+0,53072*1.E-5*TAУ2+0.883*1.E-7*TAУ3
TETA=0.97171735*1.Е-2*ТАУ-0.20685*1.Е-5*ТАУ2-0.2028*
*1.Е-6*ТАУ3
SDZ=SIN (DZETA)
CDZ=COS (DZETA)
SZ=SIN (Z)
CZ=COS (Z)
ST=SIN (TETA)
CT=COS (TETA)
PM (1, 1)=CDZ*CZ*CT-SDZ*SZ
PM (1, 2)=-SDZ*CZ*CT-CDZ*SZ
PM (1, 3)=-CZ*ST
PM (2, 1)=CDZ*SZ*CT+SDZ*CZ
PM (2, 2)=-SDZ*SZ*CT+CDZ*CZ
PM (2, 3)=-SZ*ST
PM (3,1)=CDZ*ST
PM (3, 2)=-SDZ*ST
PM (3,3)=CT
RETURN
END
     

C

********** ********** ********** ********** ********** *******
SUBROUTINE RMUMAT (D, NP1, RM)
DIMENSION RM (3, 3)
TAУ=D/36525.
MU=0.02236172*TAУ+0.67707*1.E-5*TAУ*TAУ+0.1755*1.E-6*
*ТАУ*ТАУ*ТАУ
CALL НУТАС (D, NP1, HP, HE, E, EO)
HALFA=HP*COS (E)
SMUHA=SIN (MU+HALFA)
CMUHA=COS (MU+HALFA)
RM (1, 1)=CMUHA
RM (1, 2)=SMUHA
RM (1, 3)=0.
RM (2, 1)=-SMUHA
RM (2, 2)=CMUHA
RM (2, 3)=0.
RM (3, 1)=0.
RM (3, 2)=0.
RM (3, 3)=1.
RETURN
END

     
     
ПРИЛОЖЕНИЕ 4
Справочное

ПРИМЕРЫ РАСЧЕТА МАТРИЦ ПРЕЦЕССИИ, НУТАЦИИ И ЗВЕЗДНОГО ВРЕМЕНИ

     Пример 1.
     

ИСХОДНЫЕ ДАННЫЕ

NDMG=6051988

Т (UT1)=0.00

NP1=0

NP2=0

РЕЗУЛЬТАТЫ СЧЕТА

JD=2447287

DJD=5.0000-01

D=-4.257500000+03

DM=0.0000+0

SI=3.910713393+00

SС=3.910706227+00

SM=3.913312726+00

МАТРИЦА НУТАЦИИ НМ

9.9999999997-01

-7.1659192628-06

-3.1070314463-06

7.1657857874-06

9.9999999905-01

-4.2957047299-05

3.1073392701-06

4.2957022742-05

9.9999999907-01

МАТРИЦА ПРЕЦЕССИИ РМ

9.9999596162-01

2.6064761738-03

1.1326991650-03

-2.6064761739-03

9.9999660313-01

-1.4761500974-06

-1.1326991650-03

-1.4762092497-06

9.9999935849-01

МАТРИЦА RMU

9.9999999997-01

7.1657857874-06

0.0000000000+00

-7.1657857874-06

9.9999999997-01

0.0000000000+00

0.0000000000+00

0.0000000000+00

1.0000000000+00

МАТРИЦА Р=НМ*РМ

9.9999598378-01

2.5993102834-03

1.1295921461-03

-2.5992617571-03

9.9999662091-01

-4.4425053158-05

-1.1297038036-03

4.1488766780-05

9.9999936102-01

     
     
     Пример 2.
     

ИСХОДНЫЕ ДАННЫЕ

NDMG=6051988

Т (UT1)=153045.15

NP1=0

NP2=0

РЕЗУЛЬТАТЫ СЧЕТА

JD=2447288

DM=6.463559029-0

DJD=1.463559028-01

D=-4.2568536445+03

SI=1.699821523+00

SC=1.699813936+00

SM=1.702420040+00

МАТРИЦА НУТАЦИИ НМ

9.9999999996-01

-7.5873659227-06

-3.2897641450-06

7.5872245852-06

9.9999999905-01

-4.2960700284-05

3.2900901005-06

4.2960672545-05

9.9999999907-01

МАТРИЦА ПРЕЦЕССИИ РМ

9.9999596285-01

2.6060804853-03

1.1325271999-03

-2.6060804853-03

9.9999660416-01

-1.4757019335-06

-1.1325271998-03

-1.4757610589-06

9.9999935869-01

МАТРИЦА RMU

9.9999999997-01

7.5872245852-06

0.0000000000+00

-7.5872245852-06

9.9999999997-01

0.0000000000+00

0.0000000000+00

0.0000000000+00

1.0000000000+00

МАТРИЦА Р=НМ*РМ

9.9999598631-01

2.5984931499-03

1.1292374490-03

-2.5984446347-03

9.9999662304-01

-4.4427781927-05

-1.1293490809-03

4.1493339839-05

9.9999936142-01

     
     
     Пример 3.
     

ИСХОДНЫЕ ДАННЫЕ

NDMG=23061987

T (UT1)=0.00

NP1=0

NP2=0

РЕЗУЛЬТАТЫ СЧЕТА

JD=2446969

DM=0.000000000+0

DJD=5.000000000-01

D=-4.575500000+03

SI=4.723393770+00

SC=4.723403754+00

SM=4.726204930+00

МАТРИЦА НУТАЦИИ НМ

9.9999999994-01

9.9845949170-06

4.3291889303-06

-9.9844175856-06

9.9999999911-01

-4.0959898342-05

-4.3295978945-06

4.0959853322-05

9.9999999915-01

МАТРИЦА ПРЕЦЕССИИ РМ

9.9999533584-01

2.8011503947-03

1.2173044165-03

-2.8011503948-03

9.9999607676-01

-1.7048936386-06

-1.2173044164-03

-1.7049670601-06

9.9999925908-01

МАТРИЦА RMU

9.9999999995-01

-9.9844175857-06

0.0000000000+00

9.9844175857-06

9.9999999995-01

0.0000000000+00

0.0000000000+00

0.0000000000+00

1.0000000000+00

МАТРИЦА Р=НМ*РМ

9.9999530254-01

2.8111349429-03

1.2216335851-03

-2.8110849026-03

9.9999604797-01

-4.2676915707-05

-1.2217487277-03

3.9242597714-05

9.9999925289-01

     
     
     Пример 4.
     

ИСХОДНЫЕ ДАННЫЕ

NDMG=23061987

T (UT1)= 121212.00

NP1=0

NP2=0

РЕЗУЛЬТАТЫ СЧЕТА

JD=2446970

DM=5.084722222-01

DJD=8.472222222-03

D=-4.574991531+03

SI=1.643780943+00

SC=1.643790723+00

SM=1.646591587+00

МАТРИЦА НУТАЦИИ НМ

9.9999999994-01

9.7803786014-06

4.2406433872-06

-9.7802053348-06

9.9999999911-01

-4.0856676151-05

-4.2410429773-06

4.0856632950-05

9.9999999915-01

МАТРИЦА ПРЕЦЕССИИ РМ

9.9999533688-01

2.8008391198-03

1.2171691360-03

-2.8008391198-03

9.9999607764-01

-1.7045147415-06

-1.2171691359-03

-1.7045881385-06

9.9999925925-01

МАТРИЦА RMU

9.9999999995-01

-9.7802053348-06

0.0000000000+00

9.7802053348-06

9.9999999995-01

0.0000000000+00

0.0000000000+00

0.0000000000+00

1.0000000000+00

МАТРИЦА Р=НМ*РМ

9.9999530427-01

2.8106194526-03

1.2214097595-03

-2.8105695476-03

9.9999604942-01

-4.2573064790-05

-1.2215245909-03

3.9140006079-05

9.9999925317-01

  отправить на печать

Личный кабинет:

доступно после авторизации

Календарь налогоплательщика:

ПнВтСрЧтПтСбВс
01 02
03 04 05 06 07 08 09
10 11 12 13 14 15 16
17 18 19 20 21 22 23
24 25 26 27 28

Заказать прокат автомобилей в Краснодаре со скидкой 15% можно через сайт нашего партнера – компанию Автодар. http://www.avtodar.ru/

«Я не ожидала, что стану участницей шоу еще раз»:...
Создайте свой интернет-магазин на новой платформе ReadyScript
Хостинг, домены, VPS/VDS, размещение серверов
Что это?
RuFox.ru - голосования онлайн
добавить голосование

наверх
© 2007-2025 ООО «РуФокс» о проекте вакансии хостинг создание сайтов реклама на сайте наши партнеры сообщить об ошибке