- USD ЦБ 03.12 30.8099 -0.0387
- EUR ЦБ 03.12 41.4824 -0.0244
|
Краснодар:
|
погода |
Курсы
Индексы
- DJIA 03.12 12019.4 -0.01
- NASD 03.12 2626.93 0.03
- RTS 03.12 1545.57 -0.07
ГОСТ Р 50779.27-2007
(МЭК 61649:1997)
Группа Т59
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
КРИТЕРИЙ СОГЛАСИЯ И ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ
ДЛЯ РАСПРЕДЕЛЕНИЯ ВЕЙБУЛЛА
Statistical methods. Goodness-of-fit tests and confidence intervals
for Weibull distributed data
ОКС 03.120.30
Дата введения 2008-06-01
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. N 184-ФЗ "О техническом регулировании", а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 "Стандартизация в Российской Федерации. Основные положения"
Сведения о стандарте
1 ПОДГОТОВЛЕН Открытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (ОАО "НИЦ КД") и Техническим комитетом по стандартизации ТК 125 "Статистические методы в управлении качеством продукции" на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2 ВНЕСЕН Управлением развития, информационного обеспечения и аккредитации Федерального агентства по техническому регулированию и метрологии
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 14 ноября 2007 г. N 303-ст
4 Настоящий стандарт является модифицированным по отношению к международному стандарту МЭК 61649:1997 "Критерии согласия, доверительные интервалы и нижние доверительные границы для распределения Вейбулла" (IEC 61649:1997 "Goodness-of-fit tests, confidence intervals and lower confidence limits for Weibull distributed data") путем внесения технических отклонений, объяснение которых приведено во введении к настоящему стандарту.
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5)
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе "Национальные стандарты", а текст изменений и поправок - в ежемесячно издаваемых информационных указателях "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
Введение
Наработки до отказа невосстанавливаемых объектов, для которых интенсивность отказов во времени монотонно возрастает или убывает, обычно подчиняются распределению Вейбулла. Причинами такого поведения интенсивности отказов обычно является наличие в исследуемом объекте процессов износа или ранних отказов, вызванных недостатками конструкции или процессов производства. Настоящий стандарт применим также и к другим случайным величинам, подчиняющимся распределению Вейбулла.
В настоящем стандарте приведен один критерий согласия, однако, для распределения Вейбулла допускается применять и другие критерии согласия. При выборе критерия разработчик должен учитывать объем выборки и другие особенности задачи. В настоящем стандарте проблема выбора критерия согласия не рассматривается.
Приведенные в настоящем стандарте методы определения доверительных интервалов ориентированы на ограниченный набор значений доверительной вероятности. При необходимости использовать другие значения доверительной вероятности для определения квантилей (нормированного нормального распределения, ![]() -распределения Стьюдента,
-распределения Стьюдента, ![]() -распределения) рекомендуется применять соответствующие таблицы (например см. [11]).
-распределения) рекомендуется применять соответствующие таблицы (например см. [11]).
В отличие от применяемого международного стандарта в настоящий стандарт не включены ссылки на МЭК 60050-191:1990 "Международный электротехнический словарь. Глава 191. Надежность и качество услуг", который нецелесообразно применять в национальном стандарте из-за отсутствия принятого гармонизированного национального стандарта. В соответствии с этим изменено содержание раздела 3. Ссылки на национальные стандарты выделены в тексте курсивом.
1 Область применения
Настоящий стандарт устанавливает расчетные и графические методы проверки соответствия наработок до отказа распределению Вейбулла, методы определения оценок максимального правдоподобия, а также приближенные методы определения границ доверительных интервалов для параметров двухпараметрического распределения Вейбулла. Кроме того, стандарт устанавливает метод определения нижних доверительных границ для вероятности безотказной работы и 10%-ных квантилей распределения.
Настоящий стандарт применим в тех случаях, когда объекты случайной выборки подвергаются испытаниям для оценки показателей надежности совокупности, из которой отобрана эта выборка. При этом в процессе испытаний фиксируют наработки до отказа.
2 Нормативные ссылки
В настоящем стандарте использованы ссылки на следующие стандарты:
ГОСТ Р 50779.10-2000 (ИСО 3534-1:1993) Статистические методы. Вероятность и основы статистики. Термины и определения (ИСО 3534-1:2006 "Статистика. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в вероятностных задачах", IDT)
ГОСТ Р 50779.21-2004 Статистические методы. Правила определения и методы расчета статистических характеристик по выборочным данным. Часть 1. Нормальное распределение (ИСО 2854:1976 "Статистическое представление данных. Методы оценки и проверки гипотез о средних и дисперсиях", NEQ)
ГОСТ Р 50779.26-2007 (МЭК 60605-4:2001) Статистические методы. Точечные оценки, доверительные, предикционные и толерантные интервалы для экспоненциального распределения (МЭК 60605-4:2001 "Испытания оборудования на надежность. Часть 4. Статистические процедуры для экспоненциального распределения. Точечные оценки, доверительные, предикционные и толерантные интервалы", MOD)
ГОСТ Р МЭК 60605-6-2007 Надежность в технике. Критерии проверки постоянства интенсивности отказов или параметра потока отказов (МЭК 60605-6:1997 "Испытания оборудования на надежность. Часть 6. Критерии проверки постоянства интенсивности отказов или параметра потока отказов", IDT)
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодно издаваемому информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом, следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
3 Термины, определения и условные обозначения
3.1 В настоящем стандарте применены термины по ГОСТ Р 50779.10.
3.2 В настоящем стандарте применены следующие условные обозначения:
|
|
- |
общее количество испытуемых объектов (объем выборки); |
|
|
- |
количество отказавших объектов (цензурирующее количество отказов), ( |
|
|
- |
наработка до |
|
|
- |
время прекращения испытаний; |
|
|
- |
уровень значимости; (1- |
|
|
- |
отношение |
|
|
- |
параметр масштаба распределения Вейбулла; |
|
|
- |
параметр формы распределения Вейбулла; |
|
|
- |
вероятность безотказной работы для распределения Вейбулла: |
|
|
- |
среднее время, за которое откажет 10% объектов совокупности (10%-ный квантиль распределения); |
|
|
- |
статистика критерия согласия; |
|
|
|
квантиль уровня |
|
|
- |
квантиль уровня |
|
|
- |
квантиль уровня |
|
|
- |
квантиль |
4 Требования
Критерий согласия![]() используют в тех случаях, когда необходимо установить соответствие данных распределению Вейбулла. Критерий согласия может быть выполнен на основе предыдущего опыта или технических заключений. В этом случае оценки параметров, доверительные интервалы и нижние доверительные границы показателей надежности могут быть получены без предварительного выполнения критерия согласия.
используют в тех случаях, когда необходимо установить соответствие данных распределению Вейбулла. Критерий согласия может быть выполнен на основе предыдущего опыта или технических заключений. В этом случае оценки параметров, доверительные интервалы и нижние доверительные границы показателей надежности могут быть получены без предварительного выполнения критерия согласия.
______________
![]() Критерий согласия - статистический критерий проверки гипотезы о соответствии данных теоретическому распределению.
Критерий согласия - статистический критерий проверки гипотезы о соответствии данных теоретическому распределению.
Приведенные в настоящем стандарте статистические методы, используемые в критерии согласия при определении доверительных интервалов для параметров распределения Вейбулла и нижних доверительных границ показателей надежности, применимы, если в процессе испытаний зафиксировано не менее 10 отказов.
Если в процессе испытаний зафиксировано менее 10 наработок до отказа, то необходимо использовать графический метод по ГОСТ Р МЭК 60605-6. Он позволяет визуально обнаружить отклонение данных от распределения Вейбулла.
5 Предположения и условия
Выборка из ![]() невосстанавливаемых объектов, взятых из одной и той же генеральной совокупности, поставлена на испытания в заданный момент времени
невосстанавливаемых объектов, взятых из одной и той же генеральной совокупности, поставлена на испытания в заданный момент времени ![]() 0. Условия испытаний должны быть одинаковыми для всех объектов, подвергаемых испытаниям. Отказавшие объекты не заменяют. Испытания прекращают в момент времени
0. Условия испытаний должны быть одинаковыми для всех объектов, подвергаемых испытаниям. Отказавшие объекты не заменяют. Испытания прекращают в момент времени ![]() . При окончании испытаний имеется
. При окончании испытаний имеется ![]() отказавших объектов. Значение
отказавших объектов. Значение ![]() больше или равно
больше или равно ![]() . Наработка до отказа каждого отказавшего объекта должна быть известна. Таким образом, имеется
. Наработка до отказа каждого отказавшего объекта должна быть известна. Таким образом, имеется ![]() наработок до отказа:
наработок до отказа: ![]() ,
, ![]() ,...,
,..., ![]() причем
причем ![]() ;
; ![]() 1, 2,...,
1, 2,..., ![]() .
.
Примечание - Статистические процедуры настоящего стандарта предполагают использование вычислительных средств. Хотя большая часть вычислений может быть выполнена на программируемом калькуляторе, рекомендуется использовать компьютер.
6 Ограничения и точность
Приведенные в настоящем стандарте методы используют, если в процессе испытаний зафиксировано не менее 10 отказов. Методы определения доверительных интервалов являются приближенными. Анализ точности этих методов приведен в приложении С. Ситуация многократно цензурированных выборок в настоящем стандарте не рассмотрена.
7 Входные и выходные данные
В качестве исходных данных приведенные методы используют наработки до отказа невосстанавливаемых объектов, которые подвергнуты испытаниям. Эти наработки до отказа должны быть известны точно, а не в виде интервала значений. Испытания могут быть завершены до того, как отказали все объекты (однократное цензурирование). Все объекты должны быть в работоспособном состоянии в начале испытаний. Испытания должны быть прекращены для всех работоспособных объектов одновременно.
Входные данные:
- количество испытуемых объектов (объем выборки) ![]() ;
;
- наработки до отказа всех отказавших объектов, расположенные в порядке возрастания (неубывания) - ![]() ,
, ![]() ,┘,
,┘, ![]() ;
;
- заданный уровень значимости ![]() или заданный уровень доверия (
или заданный уровень доверия (![]() ).
).
Выходные данные:
- решение, принятое на основании критерия согласия (принять/отклонить);
- точечные оценки и доверительные интервалы параметров масштаба и формы - ![]() и
и ![]() ;
;
- точечная оценка средней наработки до отказа;
- нижняя доверительная граница среднего времени, за которое откажет 10% совокупности объектов ![]() ;
;
- нижняя доверительная граница вероятности безотказной работы ![]() .
.
8 Методы
8.1 Критерий согласия
Шаг 1. Располагают ![]() наработок до отказа в порядке возрастания (неубывания) и вычисляют натуральные логарифмы этих наработок
наработок до отказа в порядке возрастания (неубывания) и вычисляют натуральные логарифмы этих наработок ![]() ,
, ![]() ,┘,
,┘, ![]() .
.
Примечание - ![]() .
.
Шаг 2. Вычисляют ![]() для
для ![]() :
:
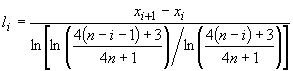 .
.
Шаг 3. На основе значений, полученных на шаге 2, вычисляют ![]() :
:
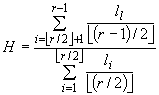 .
.
Символ ![]() использован для обозначения наибольшего целого числа, не превосходящего
использован для обозначения наибольшего целого числа, не превосходящего ![]() .
.
Шаг 4. Если ![]() , гипотезу о том, что данные соответствуют распределению Вейбулла при уровне значимости
, гипотезу о том, что данные соответствуют распределению Вейбулла при уровне значимости ![]() 100%, отклоняют и завершают анализ.
100%, отклоняют и завершают анализ.
В противном случае нет оснований для отклонения гипотезы о соответствии наработок до отказа распределению Вейбулла, и анализ может быть продолжен.
Значения квантилей ![]() -распределения приведены в ГОСТ Р 50779.21 (таблицы Г.1-Г.9).
-распределения приведены в ГОСТ Р 50779.21 (таблицы Г.1-Г.9).
Примечание - В случае отклонения гипотезы рекомендуется использовать графическое отображение данных для выявления в совокупности аномальных наработок до отказа или других выбросов. Анализ этих ситуаций выходит за рамки настоящего стандарта.
8.2 Определение оценок
8.2.1 Оценка параметров распределения
8.2.1.1 Точечные оценки ![]() и
и ![]()
Оценку максимального правдоподобия (MLE![]() ) для параметров распределения Вейбулла получают в результате решения приведенного ниже уравнения. Значение
) для параметров распределения Вейбулла получают в результате решения приведенного ниже уравнения. Значение ![]() , которое удовлетворяет первому уравнению, является оценкой максимального правдоподобия
, которое удовлетворяет первому уравнению, является оценкой максимального правдоподобия ![]() . Ее используют во втором уравнении для получения оценки максимального правдоподобия
. Ее используют во втором уравнении для получения оценки максимального правдоподобия ![]() .
.
______________
![]() MLE - Maximum Likelihood Estimate.
MLE - Maximum Likelihood Estimate.
Примечание - Для решения уравнения можно использовать компьютерную программу.
Шаг 1. Находят значение ![]() , удовлетворяющее следующему уравнению:
, удовлетворяющее следующему уравнению:
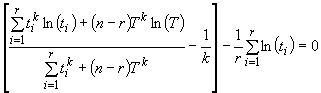 .
.
Решение этого уравнения - ![]() .
.
Шаг 2. Вычисляют ![]() , используя значение
, используя значение ![]() , полученное на шаге 1:
, полученное на шаге 1:
 .
.
8.2.1.2 Интервальная оценка параметра ![]()
Шаг 1. Вычисляют константы ![]() ,
, ![]() и
и ![]() , используя отношение
, используя отношение ![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() - квантиль уровня
- квантиль уровня ![]() -распределения с
-распределения с ![]() степенями свободы.
степенями свободы.
Поскольку число степеней свободы ![]() может быть не целым числом, для вычисления квантиля
может быть не целым числом, для вычисления квантиля ![]() -распределения необходимо использовать компьютерную программу или интерполяцию по ГОСТ Р 50779.21 (таблица В.1) или по ГОСТ Р 50779.26 (таблица D.1).
-распределения необходимо использовать компьютерную программу или интерполяцию по ГОСТ Р 50779.21 (таблица В.1) или по ГОСТ Р 50779.26 (таблица D.1).
Шаг 2. Вычисляют коэффициенты ![]() и
и ![]() :
:
 ;
; 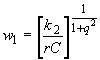 .
.
Шаг 3. Вычисляют доверительный интервал для ![]() , соответствующий уровню доверия (
, соответствующий уровню доверия (![]() ) 100%:
) 100%:
![]() .
.
Примечание - Так как значение ![]() характерно для износа, а значение
характерно для износа, а значение ![]() указывает на наличие ранних отказов, доверительный интервал для
указывает на наличие ранних отказов, доверительный интервал для ![]() допускается использовать для проверки этих предположений. Наоборот, если доверительный интервал для
допускается использовать для проверки этих предположений. Наоборот, если доверительный интервал для ![]() включает значение
включает значение ![]() 1, контролируемые объекты могут принадлежать генеральной совокупности с постоянной интенсивностью отказов. Формальный метод проверки постоянства интенсивности отказов приведен в ГОСТ Р МЭК 60605-6.
1, контролируемые объекты могут принадлежать генеральной совокупности с постоянной интенсивностью отказов. Формальный метод проверки постоянства интенсивности отказов приведен в ГОСТ Р МЭК 60605-6.
8.2.1.3 Интервальная оценка параметра ![]()
Шаг 1. Вычисляют константы ![]() ,
, ![]() и
и ![]() , используя отношение
, используя отношение ![]() :
:
![]() ;
;
![]() ;
;
![]() .
.
Шаг 2. Выполняют шаг 2![]() , если испытания завершены до отказа всех объектов, т.е.
, если испытания завершены до отказа всех объектов, т.е. ![]() . Выполняют шаг
. Выполняют шаг ![]() , если известны наработки до отказа всех объектов, т.е.
, если известны наработки до отказа всех объектов, т.е. ![]() .
.
Шаг 2![]() . Вычисляют константы
. Вычисляют константы ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() , если (
, если (![]() ):
):
![]() ,
,
где ![]() ;
;
![]() - квантиль уровня
- квантиль уровня ![]() нормированного нормального распределения, определяемый по таблице А.2;
нормированного нормального распределения, определяемый по таблице А.2;
 ;
;  ,
,
![]() ;
; ![]() .
.
Переходят к выполнению шага 3.
Шаг 2![]() . Вычисляют
. Вычисляют ![]() ,
, ![]() и
и ![]() , если
, если ![]() :
:
![]() ,
,
где ![]() - квантиль уровня
- квантиль уровня ![]()
![]() -распределения Стьюдента с (
-распределения Стьюдента с (![]() ) степенями свободы, определяемый по ГОСТ Р 50779.21 (таблица Б.1), (односторонний случай);
) степенями свободы, определяемый по ГОСТ Р 50779.21 (таблица Б.1), (односторонний случай);
![]() ;
; ![]() .
.
Значение ![]() получено в соответствии с 8.2.2, шаг 1.
получено в соответствии с 8.2.2, шаг 1.
Шаг 3. Вычисляют доверительный интервал для ![]() , соответствующий уровню доверия (
, соответствующий уровню доверия (![]() ) 100%:
) 100%:
![]() .
.
Значение ![]() получено в соответствии с 8.2.1.1, шаг 2.
получено в соответствии с 8.2.1.1, шаг 2.
8.2.2 Средняя наработка до отказа
Вычисляют точечную оценку средней наработки до отказа ![]() :
:
![]() .
.
Значения ![]() и
и ![]() получены в соответствии с 8.2.1.1, шаги 1 и 2. Здесь
получены в соответствии с 8.2.1.1, шаги 1 и 2. Здесь ![]() - гамма-функция
- гамма-функция ![]() [см. ГОСТ Р 50779.10 (подраздел 1.44)]. В таблице А.1 (приложение А) приведены значения
[см. ГОСТ Р 50779.10 (подраздел 1.44)]. В таблице А.1 (приложение А) приведены значения ![]() как функции
как функции ![]() . Для значений
. Для значений ![]() , не указанных в этой таблице, рекомендуется применять интерполяцию.
, не указанных в этой таблице, рекомендуется применять интерполяцию.
Примечание - Для случаев, когда нижняя доверительная граница ![]() равна или больше 1 (случай износа), доверительный интервал для
равна или больше 1 (случай износа), доверительный интервал для ![]() можно использовать как грубую оценку доверительного интервала для средней наработки до отказа, т.к. в этом случае гамма-функция всегда находится между 0,88 и 1.
можно использовать как грубую оценку доверительного интервала для средней наработки до отказа, т.к. в этом случае гамма-функция всегда находится между 0,88 и 1.
8.2.3 Квантиль (10%)
8.2.3.1 Точечная оценка
Вычисляют ![]() , точечную оценку
, точечную оценку ![]() (время, за которое откажет 10% объектов совокупности):
(время, за которое откажет 10% объектов совокупности):
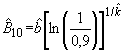 .
.
8.2.3.2 Нижняя доверительная граница
Вычисляют нижнюю доверительную границу ![]() , соответствующую уровню доверия (
, соответствующую уровню доверия (![]() ) 100%:
) 100%:
Шаг 1. Вычисляют ![]() .
.
Шаг 2. Вычисляют ![]() :
:
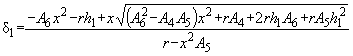 ,
,
|
где |
квантиль уровня |
Шаг 3. Вычисляют коэффициент ![]() :
:
![]() .
.
Шаг 4. Для получения нижней границы, соответствующей уровню доверия (![]() ) 100%, перемножают
) 100%, перемножают ![]() и
и ![]() :
:
![]() .
.
8.2.4 Вероятность безотказной работы за время ![]()
8.2.4.1 Точечная оценка
Вычисляют точечную оценку вероятности безотказной работы за время ![]() :
:
![]() .
.
8.2.4.2 Нижняя доверительная граница
Вычисляют нижнюю доверительную границу ![]() вероятности безотказной работы за время
вероятности безотказной работы за время ![]() , соответствующую уровню доверия (
, соответствующую уровню доверия (![]() ) 100%.
) 100%.
Шаг 1. Вычисляют константы ![]() и
и ![]() :
:
![]() ,
, ![]() .
.
Значения ![]() ,
, ![]() , и
, и ![]() вычисляют в соответствии с 8.2.1.3, шаг 1.
вычисляют в соответствии с 8.2.1.3, шаг 1.
Шаг 2. Вычисляют нижнюю доверительную границу вероятности безотказной работы за время ![]() , соответствующую уровню доверия (
, соответствующую уровню доверия (![]() ) 100%:
) 100%:
 ,
,
|
где |
квантиль уровня |
Приложение А
(справочное)
Таблицы
А.1 Таблица гамма-функции
Таблица А.1 используется при выполнении 8.2.2.
Таблица А.1 - Значения гамма-функции
|
|
|
|
0,20 |
120 |
|
0,25 |
24 |
|
0,30 |
9,2603 |
|
0,35 |
5,0295 |
|
0,40 |
3,3233 |
|
0,45 |
2,5055 |
|
0,50 |
2,0000 |
|
0,55 |
1,7024 |
|
0,60 |
1,5045 |
|
0,65 |
1,3603 |
|
0,70 |
1,2657 |
|
0,75 |
1,1906 |
|
0,80 |
1,1330 |
|
0,85 |
1,0878 |
|
0,90 |
1,0522 |
|
0,95 |
1,0238 |
|
1,00 |
1,0000 |
|
1,05 |
0,9808 |
|
1,10 |
0,9649 |
|
1,15 |
0,9517 |
|
1,20 |
0,9406 |
|
1,25 |
0,9314 |
|
1,30 |
0,9236 |
|
1,35 |
0,9169 |
|
1,40 |
0,9114 |
|
1,45 |
0,9067 |
|
1,50 |
0,9027 |
|
1,55 |
0,8994 |
|
1,60 |
0,8966 |
|
1,65 |
0,8942 |
|
1,70 |
0,8922 |
|
1,75 |
0,8906 |
|
1,80 |
0,8892 |
|
1,85 |
0,8882 |
|
1,90 |
0,8874 |
|
1,95 |
0,8867 |
|
2,00 |
0,8862 |
|
2,10 |
0,8857 |
|
2,20 |
0,8856 |
|
2,30 |
0,8859 |
|
2,40 |
0,8865 |
|
2,50 |
0,8872 |
|
2,60 |
0,8882 |
|
2,70 |
0,8893 |
|
2,80 |
0,8903 |
|
2,90 |
0,8917 |
|
3,00 |
0,8930 |
|
3,10 |
0,8943 |
|
3,20 |
0,8956 |
|
3,30 |
0,8970 |
|
3,40 |
0,8984 |
|
3,50 |
0,8997 |
|
3,60 |
0,9011 |
|
3,70 |
0,9024 |
|
3,80 |
0,9038 |
|
3,90 |
0,9051 |
|
4,00 |
0,9064 |
|
4,10 |
0,9076 |
|
4,20 |
0,9089 |
|
4,30 |
0,9101 |
|
4,40 |
0,9113 |
|
4,50 |
0,9125 |
|
4,60 |
0,9137 |
|
4,70 |
0,9149 |
|
4,80 |
0,9160 |
|
4,90 |
0,9171 |
|
5,00 |
0,9182 |
|
5,20 |
0,9202 |
|
5,40 |
0,9222 |
|
5,60 |
0,9241 |
|
5,80 |
0,9260 |
|
6,00 |
0,9277 |
|
6,20 |
0,9293 |
|
6,40 |
0,9309 |
|
6,60 |
0,9325 |
|
6,80 |
0,9340 |
|
7,00 |
0,9354 |
|
8,00 |
0,9417 |
А.2 Квантили нормированного нормального распределения
В таблице А.2 приведены значения квантилей нормированного нормального распределения ![]() для заданного значения
для заданного значения ![]() .
.
Таблица А.2 - Квантили нормированного нормального распределения
|
|
0,010 |
0,025 |
0,050 |
0,100 |
|
|
2,3263 |
1,9600 |
1,6449 |
1,2816 |
Приложение В
(справочное)
Пример
Данный пример приведен для проверки точности компьютерных программ, выполняющих расчеты в соответствии с методами настоящего стандарта.
На испытания поставлено сорок объектов. Испытания прекращены в момент 20-го отказа. Ниже приведены 20 наработок до отказа:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
10 |
17 |
32 |
32 |
33 |
34 |
36 |
54 |
55 |
55 |
58 |
58 |
61 |
64 |
65 |
65 |
66 |
67 |
68 |
Применение расчетных методов настоящего стандарта приводит к следующим результатам.
Применение критерия согласия к этому набору данных с уровнем значимости 10% не может отклонить гипотезу о соответствии этих данных распределению Вейбулла, поскольку ![]() 0,36, а
0,36, а ![]() (18; 20)=1,81.
(18; 20)=1,81.
Значения оценок максимального правдоподобия для ![]() и
и ![]() :
:
![]() 2,091 и
2,091 и ![]() 84.
84.
Доверительные интервалы, соответствующие уровню доверия 90%, - [1,34; 2,742] для ![]() и [70; 108] для
и [70; 108] для ![]() . Оценка максимального правдоподобия для
. Оценка максимального правдоподобия для ![]() :
: ![]() 28,63. Доверительная граница, соответствующая уровню доверия 90%, для
28,63. Доверительная граница, соответствующая уровню доверия 90%, для ![]() :
: ![]() 20,43.
20,43.
Значения оценки максимального правдоподобия и нижней доверительной границы для вероятности безотказной работы, соответствующей уровню доверия 90%, для трех произвольных значений ![]() :
:
|
|
|
|
|
32,46 |
0,87 |
0,80 |
|
50,00 |
0,71 |
0,62 |
|
100,00 |
0,23 |
0,12 |
Приложение С
(справочное)
Теоретическое обоснование
Данное приложение включает информацию относительно происхождения методов, использованных в настоящем стандарте. Список литературы, используемой при разработке методов настоящего стандарта, приведен в библиографии.
С.1 Критерий согласия
В настоящем стандарте приведен критерий, описанный [1]. Для вычисления ![]() в 8.1 необходимы математические ожидания экстремальных порядковых статистик. Для них использовано приближение, предложенное в [2]. В [3] показано, что критерий имеет мощность, сопоставимую с мощностью критерия Шапиро-Брейна [4] и критерия Тьюки. Последний критерий немного лучше любых критериев, использующих эмпирическую функцию распределения. Кроме того, критерий [1] может использовать цензурированные выборки.
в 8.1 необходимы математические ожидания экстремальных порядковых статистик. Для них использовано приближение, предложенное в [2]. В [3] показано, что критерий имеет мощность, сопоставимую с мощностью критерия Шапиро-Брейна [4] и критерия Тьюки. Последний критерий немного лучше любых критериев, использующих эмпирическую функцию распределения. Кроме того, критерий [1] может использовать цензурированные выборки.
С.2 Оценки максимального правдоподобия для ![]() и
и ![]()
Приведенные в настоящем стандарте уравнения обычно используют для единственной цензурированной выборки. В настоящее время это самый распространенный метод оценки параметров распределения Вейбулла. Формулы, представленные в настоящем стандарте, заимствованы из [5]. Так как расчетные методы настоящего стандарта используют только объемы выборок больше 10, статистическое смещение оценок является небольшим.
С.3 Доверительные интервалы и нижние доверительные границы
Приведенный метод заимствован из [6] для полных выборок и из [7] для цензурированных выборок. В настоящем стандарте использованы коэффициенты, полученные методами Монте Карло, и использованы асимптотические приближения результатов. Некоторые простые линейные и нелинейные функции использованы при составлении таблиц, что позволяет избавиться от вспомогательных таблиц. Отклонения во всех случаях очень малы (![]() 1%).
1%).
Другой альтернативой являются условные методы [8]. При применении этих методов расчеты являются более сложными.
Чисто асимптотический подход был отклонен, поскольку метод должен давать разумные результаты для относительно небольших выборок.
С.4 Точность стандартизированных методов
Было проведено сравнение методов настоящего стандарта с другими опубликованными методами. Все проанализированные примеры дают одинаковые с методами настоящего стандарта оценки максимального правдоподобия. Некоторые различия получены для доверительных интервалов и нижних доверительных границ (см. С.4.1 - С.4.4).
С.4.1 Метод по [7]
Поскольку этот метод является основой метода, приведенного в настоящем стандарте, объектом сравнения является точность используемых в стандарте аппроксимирующих функций. Результаты сравнения следующие:
|
|
Метод по [7] |
Метод по настоящему стандарту |
|||
|
Доверительный интервал для |
[1,34; 2,73] |
[1,34; 2,74] |
|||
|
Доверительный интервал для |
[70,7; 105,9] |
[70; 108] |
|||
|
|
0,801 |
0,800 |
|||
С.4.2 Метод по [8]
Исследуемая выборка объемом ![]() 40 включает 28 наработок до отказа. В работе [8] приведены только доверительные интервалы для
40 включает 28 наработок до отказа. В работе [8] приведены только доверительные интервалы для ![]() с уровнем доверия 90% и нижние доверительные границы с уровнем доверия 95% для
с уровнем доверия 90% и нижние доверительные границы с уровнем доверия 95% для ![]() и
и ![]() . Результаты сравнения следующие:
. Результаты сравнения следующие:
|
|
Метод по [8] |
Метод по настоящему стандарту |
|||
|
Доверительный интервал для |
[0,783; 1,381] |
[0,785; 1,370] |
|||
|
Нижняя доверительная граница с уровнем доверия 95% для |
0,066 |
0,074 |
|||
|
|
0,647 |
0,644 |
|||
С.4.3 Метод [9]
Это асимптотический метод. В качестве примера рассмотрена выборка из 96 локомотивов, 37 из них отказали. Время цензурирования ![]() немного больше, чем время последнего отказа. Так как объем выборки является довольно большим, асимптотический подход в этом случае дает хорошую точность. Авторы [9] приводят только доверительный интервал для
немного больше, чем время последнего отказа. Так как объем выборки является довольно большим, асимптотический подход в этом случае дает хорошую точность. Авторы [9] приводят только доверительный интервал для ![]() с уровнем доверия 95%, и поскольку имеется доверительный интервал для
с уровнем доверия 95%, и поскольку имеется доверительный интервал для ![]() с уровнем доверия 95%, мы можем получить нижнюю доверительную границу для этой величины с уровнем доверия 97,5%:
с уровнем доверия 95%, мы можем получить нижнюю доверительную границу для этой величины с уровнем доверия 97,5%:
|
|
Метод по [9] |
Метод по настоящему стандарту |
|
Доверительный интервал для |
[1,72; 3,16] |
[1,61; 3,04] |
|
Нижняя доверительная граница с уровнем доверия 97,5% для |
55,4 |
54,2 |
С.4.4 Метод по [10]
В работе [10] приведены таблицы, полученные методом Монте-Карло, для определения нижних доверительных границ и оценок максимального правдоподобия вероятности безотказной работы по небольшим цензурированным выборкам (![]() ). Для сравнения нижних доверительных границ использовались выборки из распределения Вейбулла, полученные с помощью датчика случайных чисел.
). Для сравнения нижних доверительных границ использовались выборки из распределения Вейбулла, полученные с помощью датчика случайных чисел.
Разница между границами, полученными в соответствии с настоящим стандартом и приведенными в [10], составила не более 1%.
Библиография
|
[1] |
Mann, N.R., Scheuer, E.M. and Fertig, K.W. (1973). A New Goodness-of-fit test for the two-parameter Weibull or Extreme Value Distribution, Commun. Stat., Vol. 2, pp. 383-400 |
|
[2] |
Blom, G. (1958). Statistical Estimates and Transformed Beta-Variables, New York, J. Wiley &Sons |
|
[3] |
Lawless, J.F. (1982). Statistical Models and Methods for Lifetime Data, New York, J. Wiley & Sons |
|
[4] |
Shapiro, S.S. and Brain, C.W., (1987). W-Test for the Weibull Distribution, Commun. Statist. -Simula., Vol. 16, No. 1, pp. 209-219 |
|
[5] |
Mann, N.R.,Schafer, E. and Singpurwalla, N. (1974). Methods for Statistical Analysis of Reliability and Lifetime Data, New York, J. Wiley & Sons |
|
[6] |
Bain, L.J. and Engelhardt, M. (1981), Simple Approximate Distributional Results for Confidence and Tolerance Limits for the Weibull Distribution Based on Maximum Likelihood Estimators, Technometrics, Vol. 23, No. 1, pp. 15-20 |
|
[7] |
Bain, L.J. and Engelhardt, M. (1986), Approximate Distributional Results Based on the Maximum Likelihood Estimators for the Weibull Distribution, Journal of Quality Technology, Vol. 18, No. 3, pp. 174-181 |
|
[8] |
Lawless, J.F. (1978). Confidence Interval Estimation for the Weibull and Extreme Value Distributions, Technometrics, Vol. 20, No. 4, pp. 355-368 |
|
[9] |
Meeker, W.Q. and Nelson, W., (1976). Weibull Percentile Estimates and Confidence Limits from Singly Censored Data by Maximum Likelihood, IEEE Trans, on Reliability, Vol. R-25, No. 1, pp. 20-24 |
|
[10] |
Guida, M., (1985). On the Confidence Limits for Weibull Reliability and Quantiles: The Case of Maximum Likelihood Estimation from Small Size Censored Samples, Reliability Engineering, Vol. 12, pp. 217-240 |
|
[11] |
Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - M.: Наука, 1983 |

 Армавирец пытался незаконно отправить в США тестостерон
Армавирец пытался незаконно отправить в США тестостерон  Создайте свой интернет-магазин на новой платформе ReadyScript
Создайте свой интернет-магазин на новой платформе ReadyScript  Хостинг, домены, VPS/VDS, размещение серверов
Хостинг, домены, VPS/VDS, размещение серверов