ГОСТ 25645.127-85
Группа Т27
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
МАГНИТОСФЕРА ЗЕМЛИ
Модель магнитного поля магнитосферных токов
Earth's magnetosphere. Magnetic field model of magnetospheric currents
ОКСТУ 0080
Дата введения 1987-01-01
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 14.11.85 N 3609
РАЗРАБОТЧИКИ СТАНДАРТА
И.И.Алексеев, канд. физ.-мат. наук; А.В.Баюков, канд. техн. наук; Е.С.Беленькая, канд. физ-.мат. наук; Н.П.Бенькова, д-р физ-мат. наук; Ю.А.Винтенко, канд. техн. наук; А.Н.Герасимов; В.П.Головков, д-р физ.-мат. наук; Е.В.Горчаков, д-р физ.-мат. наук; М.С.Григорян; И.П.Иваненко, д-р физ.-мат. наук; В.В.Калегаев; Г.И.Коломийцева, канд. физ.-мат. наук; А.П.Кропоткин, д-р физ.-мат. наук; Е.Н.Лесновский, канд. техн. наук; В.М.Ломакин, канд. техн. наук; Ю.Г.Лютов; В.В.Мигулин, чл.-кор. АН СССР; Л.И.Мирошниченко, канд. физ.-мат. наук; В.Н.Никитинский; М.И.Панасюк, д-р физ.-мат. наук; И.Я.Ремизов, канд. техн. наук; В.И.Степакин, канд. техн. наук; Л.Н.Степанова; И.Б.Теплов, д-р физ.-мат. наук; М.В.Терновская, канд. физ.-мат. наук; В.В.Хаустов, канд. техн. наук
2. СОГЛАСОВАНО с Государственной службой стандартных справочных данных (протокол от 16.06.85 N 18)
3. Срок первой проверки 1989 г.
Периодичность проверки - 5 лет.
4. ВВЕДЕН ВПЕРВЫЕ
5. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ
|
Обозначение НТД, на который дана ссылка |
Номер пункта, приложения |
|
1.4, приложения 1, 2 | |
|
2.2 |
6. ПЕРЕИЗДАНИЕ (апрель 1990 г.) с Изменением N 1, утвержденным в сентябре 1989 г. (ИУС 12, 1989)
Настоящий стандарт устанавливает модель магнитного поля токов, текущих в магнитосфере Земли и на магнитопаузе (магнитосферных токов) на геоцентрических расстояниях от 1 до 7 земных радиусов.
Стандарт предназначен для использования в расчетах при определении условий функционирования технических устройств в космическом пространстве.
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
1.1. Модель магнитного поля магнитосферных токов (далее - модель) описывает регулярную часть магнитного поля, ее зависимость от параметров межпланетной среды и отражает сжатие магнитосферы Земли на дневной стороне из-за взаимодействия с солнечным ветром, асимметрию день-ночь (поле на ночной стороне ослаблено), суточные и сезонные вариации поля.
1.2. Модель представляет вектор индукции магнитного поля магнитосферных токов как функцию от солнечно-магнитосферных координат. Она получена линейной аппроксимацией эмпирической модели, которая основана на измерениях магнитного поля на искусственных спутниках Земли.
1.3. Модель учитывает угол наклона геомагнитного диполя к плоскости ортогональной линии Земля-Солнце 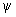 , изменяющийся в интервале от -35 до +35°.
, изменяющийся в интервале от -35 до +35°.
1.4. Вектор индукции магнитного поля  в магнитосфере Земли вычисляют по формуле
в магнитосфере Земли вычисляют по формуле
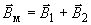 , нТл, (1)
, нТл, (1)
где 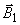 - вектор индукции геомагнитного поля внутриземных источников, вычисляемый по ГОСТ 25645.126-85 в сферической системе координат;
- вектор индукции геомагнитного поля внутриземных источников, вычисляемый по ГОСТ 25645.126-85 в сферической системе координат;
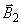 - вектор индукции магнитного поля магнитосферных токов, вычисляемый в солнечно-магнитосферной системе координат.
- вектор индукции магнитного поля магнитосферных токов, вычисляемый в солнечно-магнитосферной системе координат.
Матрица перехода из сферической системы координат в солнечно-магнитосферную систему координат приведена в справочном приложении 1.
Пример расчета  приведен в справочном приложении 2.
приведен в справочном приложении 2.
1.5. Среднее квадратическое отклонение вектора индукции 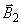 от экспериментальных данных составляет ~20 нТл.
от экспериментальных данных составляет ~20 нТл.
Сведения о нерегулярных вариациях индукции магнитного поля магнитосферных токов приведены в справочном приложении 3.
2. РАСЧЕТ ОСНОВНЫХ ПАРАМЕТРОВ МАГНИТОСФЕРЫ
2.1. Основными параметрами магнитосферы являются геоцентрическое расстояние до точки пересечения магнитопаузы линией Земля-Солнце 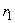 и угол наклона геомагнитного диполя к плоскости ортогональной линии Земля - Солнце
и угол наклона геомагнитного диполя к плоскости ортогональной линии Земля - Солнце 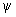 .
.
2.2. Геоцентрическое расстояние 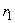 вычисляют по формуле
вычисляют по формуле
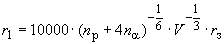 , км, (2)
, км, (2)
где 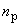 - концентрация протонов в солнечном ветре, м
- концентрация протонов в солнечном ветре, м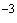 ;
;
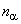 - концентрация
- концентрация 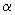 -частиц в солнечном ветре, м
-частиц в солнечном ветре, м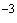 ;
;
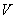 - скорость солнечного ветра, м/с;
- скорость солнечного ветра, м/с;
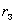 - средний радиус Земли, км.
- средний радиус Земли, км.
Примечание. Значения 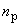 ,
, 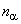 ,
, 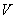 - по ГОСТ 25645.136-86.
- по ГОСТ 25645.136-86.
2.3. Угол 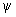 вычисляют по формуле
вычисляют по формуле
 , (3)
, (3)
где  11,0° - угол между осью вращения Земли и осью геомагнитного диполя;
11,0° - угол между осью вращения Земли и осью геомагнитного диполя;
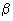 - склонение Солнца, ?°, (изменяется от -23,5 до +23,5°);
- склонение Солнца, ?°, (изменяется от -23,5 до +23,5°);
 - угол между плоскостью полуночного меридиана и меридиональной плоскостью, содержащей северный магнитный полюс, ?°;
- угол между плоскостью полуночного меридиана и меридиональной плоскостью, содержащей северный магнитный полюс, ?°;
 - всемирное время, ч;
- всемирное время, ч;
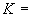 15°/ч;
15°/ч;
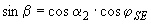 , (4)
, (4)
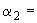 23,5° - угол наклона плоскости экватора к плоскости эклиптики;
23,5° - угол наклона плоскости экватора к плоскости эклиптики;
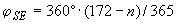 - угол между линией Земля-Солнце и проекцией оси вращения Земли на плоскость эклиптики, ?°;
- угол между линией Земля-Солнце и проекцией оси вращения Земли на плоскость эклиптики, ?°;
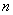 - порядковый номер дня в году (с 1 января).
- порядковый номер дня в году (с 1 января).
3. РАСЧЕТ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ МАГНИТОСФЕРНЫХ ТОКОВ
3.1. Индукцию магнитного поля магнитосферных токов вычисляют в солнечно-магнитосферной системе координат по формуле
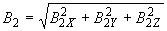 , нТл, (5)
, нТл, (5)
где 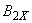 - проекция вектора
- проекция вектора 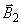 на ось
на ось  , направленную на Солнце;
, направленную на Солнце;
 - проекция вектора
- проекция вектора 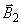 на ось
на ось 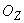 , лежащую в плоскости, проходящей через ось
, лежащую в плоскости, проходящей через ось 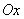 и ось геомагнитного диполя;
и ось геомагнитного диполя;
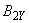 - проекция вектора
- проекция вектора 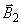 , на ось
, на ось  , дополняющую правостороннюю систему координат.
, дополняющую правостороннюю систему координат.
(Измененная редакция, Изм. N 1).
3.2. Составляющую 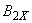 вычисляют по формуле
вычисляют по формуле
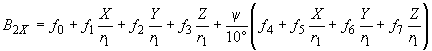 , нТл, (6)
, нТл, (6)
где
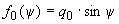 ;
;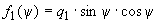 ;
;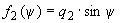 ;
; ;
; ;
;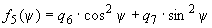 ;
; ;
; .
.
3.3. Составляющую 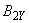 вычисляют по формуле
вычисляют по формуле
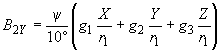 , нТл, (7)
, нТл, (7)
где
 ;
;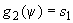 ;
;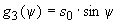 .
.
3.4. Составляющую  вычисляют по формуле
вычисляют по формуле
 , нТл, (8)
, нТл, (8)
где
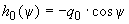 ;
; ;
;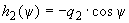 ;
; ;
; ;
;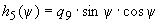 ;
;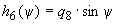 ;
;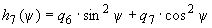 ;
;
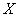 ,
, 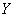 ,
, 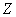 - солнечно-магнитосферные координаты в единицах
- солнечно-магнитосферные координаты в единицах 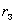 ;
;
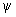 - угол наклона геомагнитного диполя, ?°.
- угол наклона геомагнитного диполя, ?°.
Значения коэффициентов 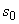 ,
, 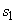 ,
, 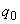 , ?,
, ?,  приведены в таблице, нТл:
приведены в таблице, нТл:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,2 |
-2,5 |
8,5 |
-39,6 |
1,2 |
21,8 |
-17,9 |
2,9 |
-3,0 |
5,5 |
0,2 |
-8,5 |
3.5. Пример программы для расчета составляющих вектора индукции магнитного поля 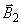 приведет в справочном приложении 4.
приведет в справочном приложении 4.
ПРИЛОЖЕНИЕ 1
Справочное
ПЕРЕВОД ВЕКТОРА ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ИЗ ГЕОГРАФИЧЕСКОЙ СИСТЕМЫ КООРДИНАТ В СОЛНЕЧНО-МАГНИТОСФЕРНУЮ
По ГОСТ 25645.126-85 вектор индукции магнитного поля 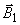 , задан в точке (
, задан в точке (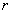 ,
, 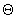 ,
, 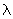 ) составляющими
) составляющими 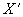 ,
, 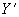 ,
, 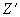 с использованием обозначений:
с использованием обозначений:
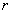 - геоцентрическое расстояние, км;
- геоцентрическое расстояние, км;
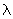 - долгота, отсчитываемая от плоскости гринвичского меридиана, ?°;
- долгота, отсчитываемая от плоскости гринвичского меридиана, ?°;
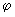 - широта, отсчитываемая от плоскости земного экватора, ?°;
- широта, отсчитываемая от плоскости земного экватора, ?°;
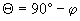 - полярный угол, ...°.
- полярный угол, ...°.
Перевод вектора из данной сферической системы координат в солнечно-магнитосферную осуществляют при помощи матрицы 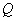 по формуле
по формуле
 , (1)
, (1)
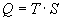 , (2)
, (2)
где  ;
; 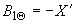 ;
;  ;
;
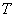 - матрица поворота к солнечно-магнитосферным координатам;
- матрица поворота к солнечно-магнитосферным координатам;
 - матрица перевода из сферических в декартовы координаты;
- матрица перевода из сферических в декартовы координаты;
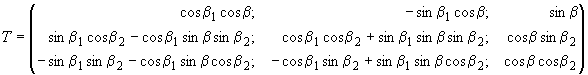 (3)
(3)
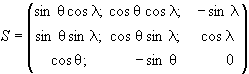 , (4)
, (4)
где  - западная долгота полуденного меридиана, ?°;
- западная долгота полуденного меридиана, ?°;
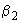 - угол между полуденным географическим меридианом и плоскостью
- угол между полуденным географическим меридианом и плоскостью 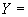 0 в солнечно-магнитосферных координатах, ?°;
0 в солнечно-магнитосферных координатах, ?°;
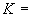 15°/ч;
15°/ч; 12 ч;
12 ч;
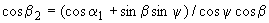 , (5)
, (5)
где  11,0° - угол наклона геомагнитного диполя к оси вращения Земли;
11,0° - угол наклона геомагнитного диполя к оси вращения Земли;
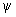 - угол наклона геомагнитного диполя к плоскости, ортогональной линии Земля-Солнце, ?°;
- угол наклона геомагнитного диполя к плоскости, ортогональной линии Земля-Солнце, ?°;
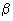 - склонение Солнца, ...°.
- склонение Солнца, ...°.
ПРИЛОЖЕНИЕ 2
Справочное
ПРИМЕР РАСЧЕТА СОСТАВЛЯЮЩИХ ВЕКТОРА ИНДУКЦИИ МАГНИТНОГО ПОЛЯ
Исходные данные:
точка с солнечно-магнитосферными координатами 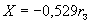 ,
,  ,
, 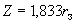 ; дата - 1 января 1985 г.; всемирное время
; дата - 1 января 1985 г.; всемирное время 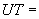 10,6 ч; параметры солнечного ветра: плотность протонов
10,6 ч; параметры солнечного ветра: плотность протонов  5·10
5·10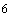 м
м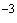 , плотность
, плотность 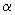 -частиц
-частиц 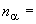 2,5·10
2,5·10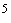 м
м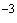 , скорость солнечного ветра
, скорость солнечного ветра 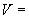 4·10
4·10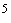 м/с.
м/с.
Порядок вычислений:
1. По формуле (3) приложения 1 настоящего стандарта вычисляют матрицу 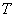
 .
.
2. Вычисление сферических координат точки осуществляют по формулам:
 ,
, 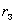 ;
;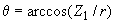 , ?°;
, ?°;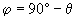 , ?°;
, ?°; , ?°,
, ?°,
где
 ,
, 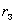 ,
,
 - транспонированная матрица
- транспонированная матрица 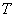 . Расчет дает
. Расчет дает
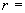 12742,4 км;
12742,4 км;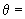 9,4°;
9,4°;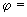 80,6°;
80,6°; 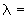 58°.
58°.
3. По ГОСТ 25645.126-85 вычисляют составляющие вектора индукции магнитного поля 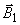 в сферической системе координат (приложение З):
в сферической системе координат (приложение З):
 нТл;
нТл;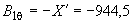 нТл;
нТл;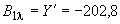 нТл.
нТл.
4. По формуле (4) приложения 1 настоящего стандарта вычисляют матрицу  :
:
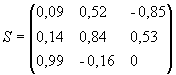
5. По формуле (1) приложения 1 настоящего стандарта вычисляют составляющие вектора индукции магнитного поля 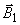 в солнечно-магнитосферной системе координат:
в солнечно-магнитосферной системе координат:
 1337,5 нТл;
1337,5 нТл; -2991,0 нТл;
-2991,0 нТл;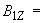 - 6763,6 нТл.
- 6763,6 нТл.
6. По формуле (2) настоящего стандарта вычисляют геоцентрическое расстояние до точки пересечения магнитопаузы линией Земля-Солнце 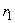 :
:
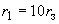 .
.
7. По формуле (3) настоящего стандарта вычисляют угол наклона геомагнитного диполя к плоскости, ортогональной линии Земля-Солнце, 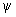 :
:
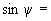 0,383;
0,383; 22,5°.
22,5°.
8. По формулам (6)-(8) настоящего стандарта вычисляют составляющие вектора индукции магнитного поля 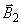 в солнечно-магнитосферной системе координат:
в солнечно-магнитосферной системе координат:
 12,0 нТл;
12,0 нТл;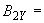 -0,4 нТл;
-0,4 нТл;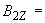 -1,3 нТл.
-1,3 нТл.
9. По формуле (1) настоящего стандарта вычисляют составляющие вектора индукции магнитного поля  в солнечно-магнитосферной системе координат:
в солнечно-магнитосферной системе координат:
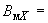 1349,5 нТл;
1349,5 нТл;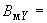 -2991,4 нТл;
-2991,4 нТл;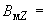 -6764,9 нТл.
-6764,9 нТл.
Примечание. Если исходная точка задана в сферической системе координат, то в п.2 настоящего приложения вычисляют ее солнечно-магнитосферные координаты по формулам:
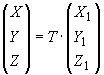 ,
,
где
ПРИЛОЖЕНИЕ 3
Справочное
НЕРЕГУЛЯРНЫЕ ВАРИАЦИИ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ
1. Нерегулярные вариации вектора индукции магнитного поля магнитосферных токов, не учитываемые моделью, при магнитной буре составляют ~100 нТл, а в спокойное время ~10 нТл.
2. Нерегулярные вариации вектора индукции магнитного поля от ионосферных и продольных токов, также не учитываемые моделью, существенны на высотах до 1000 км и имеют значения порядка 50 нТл на геомагнитных широтах до 60 и свыше 80°, и 500 нТл - на широтах от 60 до 80°.
ПРИЛОЖЕНИЕ 4
Справочное
ПРИМЕР ПРОГРАММЫ ДЛЯ РАСЧЕТА
СОСТАВЛЯЮЩИХ ВЕКТОРА ИНДУКЦИИ МАГНИТНОГО ПОЛЯ 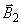
Входные параметры:
ХХ(3) - солнечно-магнитосферные координаты точки в пространстве;
R1 - расстояние от Земли до точки пересечения магнитопаузы линией Земля-Солнце;
PSI - угол наклона геомагнитного диполя.
Выходные параметры: B(3) - составляющие вектора индукции магнитного поля 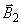 .
.
|
0001 |
DIMENSION XX(3), B(3), F(8), G(3), H(8), Q(10) | |||
|
0002 |
|
DATA S0, S1/-0,18, -2.51/, Q/8.52, -39.65, 1.25, | ||
|
С |
||||
|
С |
1. |
ЗАДАНИЕ СОЛНЕЧНО-МАГНИТОСФЕРНЫХ КООРДИНАТ | ||
|
|
С |
ТОЧКИ (В R3) | ||
|
0003 |
DATA XX/-0.530, 0.609, 1.834/ | |||
|
С |
||||
|
С |
2. |
ЗАДАНИЕ УГЛА НАКЛОНА ГЕОМАГНИТНОГО ДИПОЛЯ, | ||
|
С |
РАССЧИТАННОГО НА ЗАДАННЫЙ ДЕНЬ ПО ФОРМУЛЕ (3) | |||
|
0004 |
PSI=22.5258 | |||
|
С |
||||
|
С |
3. |
ЗАДАНИЕ ГЕОЦЕНТРИЧЕСКОГО РАССТОЯНИЯ (В R3), | ||
|
С |
РАССЧИТАННОГО ПО ФОРМУЛЕ (2) | |||
|
0005 |
R1=10. | |||
|
С |
||||
|
0006 |
PS=PSI/10. | |||
|
0007 |
PSY=PSI*3.1415926/180. | |||
|
0008 |
SP=SIN(PSY) | |||
|
0009 |
CP=COS(PSY) | |||
|
0010 |
F(1)=Q(1)*SP | |||
|
0011 |
F(2)=Q(2)*SP*CP | |||
|
0012 |
F(3)=Q(3)*SP | |||
|
0013 |
F(4)=Q(4)*CP*CP+Q(5)*SP*SP | |||
|
0014 |
F(5)=Q(6)*CP | |||
|
0015 |
F(6) =Q(7)*CP*CP+Q(8)*SP*SP | |||
|
0016 |
F(7)=Q(9)*CP | |||
|
0017 |
F(8)=Q(10)*SP*CP | |||
|
0018 |
G(1)=SO*CP | |||
|
0019 |
G(2)=S1 | |||
|
0020 |
G(3)=SO*CP | |||
|
0021 |
H(1)=-Q(1)*CP | |||
|
0022 |
H(2)=-Q(4)*SP*SP-Q(5)*CP*CP | |||
|
0023 |
H(3)=-Q(3)*CP | |||
|
0024 |
H(4)=-Q(2)*CP*SP | |||
|
0025 |
H(5)=Q(6)*SP | |||
|
0026 |
H(6)=Q(10)*CP*SP | |||
|
0027 |
H(7)=Q(9)*SP | |||
|
0028 |
H(8)=Q(7)*SP*SP+Q(8)*СP*СP | |||
|
0029 |
X=XX(1)/R1 | |||
|
0030 |
Y=XX(2)/R1 | |||
|
0031 |
Z=XX(3)/R1 | |||
|
0032 |
B(1)=F(1)+X*F2+Y*F(3)+Z*F(4)+PS*(F(5)+ X*F(6) | |||
|
*+Y*F(7)+Z*F(8)) | ||||
|
0033 |
B(2)=PS*(X*G(1)+Y*G(2)+Z*G(3)) | |||
|
0034 |
B(3)=H(1)+X*H(2)+Y*H(3)+Z*H(4)+PS*(H(5)+X*H(6) | |||
|
*+Y*H(7)+Z*H(8)) | ||||
|
0035 |
PRINT 200, XX, R1, PSI, В | |||
|
0036 |
200 FORMAT (//, 16X, 'X', 9X, 'Y', 9X, 'Z', 9X, 'R1', 7X | |||
|
*'PSI', 8X, 'BX', 8X, 'BY', 8X, 'BZ', //, 10Х, 8F10.4) | ||||
|
0037 |
STOP | |||
|
0038 |
END | |||
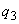
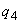



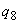
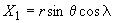 ,
, 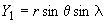 ,
,  ,
,