- USD ЦБ 03.12 30.8099 -0.0387
- EUR ЦБ 03.12 41.4824 -0.0244
|
Краснодар:
|
погода |
Курсы
Индексы
- DJIA 03.12 12019.4 -0.01
- NASD 03.12 2626.93 0.03
- RTS 03.12 1545.57 -0.07
РМГ 43-2001
Группа Т80
РЕКОМЕНДАЦИИ ПО МЕЖГОСУДАРСТВЕННОЙ СТАНДАРТИЗАЦИИ
Государственная система обеспечения единства измерений
ПРИМЕНЕНИЕ "РУКОВОДСТВА
ПО ВЫРАЖЕНИЮ НЕОПРЕДЕЛЕННОСТИ ИЗМЕРЕНИЙ"
МКС 17.020
Дата введения 2003-07-01
Предисловие
1 РАЗРАБОТАНЫ Всероссийским научно-исследовательским институтом метрологии им. Д.И.Менделеева (ВНИИМ им. Д.И.Менделеева) Госстандарта России
ВНЕСЕНЫ Госстандартом России
2 ПРИНЯТЫ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол N 20 от 2 ноября 2001 г.)
За принятие проголосовали:
|
Наименование государства |
Наименование национального органа |
|
Азербайджанская Республика |
Азгосстандарт |
|
Республика Армения |
Армгосстандарт |
|
Республика Беларусь |
Госстандарт Республики Беларусь |
|
Грузия |
Грузстандарт |
|
Республика Казахстан |
Госстандарт Республики Казахстан |
|
Кыргызская Республика |
Кыргызстандарт |
|
Республика Молдова |
Молдовастандарт |
|
Российская Федерация |
Госстандарт России |
|
Республика Таджикистан |
Таджикстандарт |
|
Туркменистан |
Главгосслужба "Туркменстандартлары" |
|
Республика Узбекистан |
Узгосстандарт |
|
Украина |
Госстандарт Украины |
3 Постановлением Государственного комитета Российской Федерации по стандартизации и метрологии от 26 марта 2003 г. N 96-ст рекомендации по метрологии РМГ 43-2001 введены в действие непосредственно в качестве Рекомендаций по метрологии Российской Федерации с 1 июля 2003 г.
4 ВВЕДЕНЫ ВПЕРВЫЕ
Введение
В 1993 г. под эгидой Международного комитета мер и весов (МКМВ), Международной электротехнической комиссии (МЭК), Международной организации по стандартизации (ИСО), Международной организации по законодательной метрологии (МОЗМ), Международного союза по чистой и прикладной физике, Международного союза по чистой и прикладной химии и Международной федерации клинической химии разработано "Руководство по выражению неопределенности измерения" (далее - Руководство).
Целями Руководства являются:
- обеспечение полной информации о том, как составлять отчеты о неопределенностях измерений;
- предоставление основы для международного сопоставления результатов измерений;
- предоставление универсального метода для выражения и оценивания неопределенности измерений, применимого ко всем видам измерений и всем типам данных, которые используются при измерениях.
Существуют два подхода к оцениванию параметров (характеристик) точности измерений. Один подход основан на понятиях и терминах, используемых в Руководстве, другой - на понятиях и терминах, применяемых в основополагающих нормативных документах (НД) в области метрологии, используемых в национальных системах обеспечения единства измерений государств - участников Соглашения "О проведении согласованной политики в области стандартизации, метрологии и сертификации" (далее - Соглашение).
Задачами настоящих рекомендаций являются:
- изложение основных положений Руководства и рекомендаций по их практическому применению;
- сравнительный анализ двух подходов к описанию точности измерений;
- показ соответствия между формами представления результатов измерений, используемыми в основополагающих НД в области метрологии, и формой, используемой в Руководстве.
1 Область применения
Настоящие рекомендации распространяются на методы оценивания точности результатов измерений, содержат практические рекомендации по применению Руководства [1] и показывают соответствие между формами представления результатов измерений, принятыми в основополагающих нормативных документах (НД) по метрологии, применяемых в странах - участниках Соглашения, и формой, принятой в Руководстве.
2 Нормативные ссылки
В настоящих рекомендациях использованы ссылки на следующие стандарты и рекомендации:
ГОСТ 8.207-76 Государственная система обеспечения единства измерений. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения
ГОСТ 8.381-80 Государственная система обеспечения единства измерений. Эталоны. Способы выражения погрешностей
РМГ 29-99 Государственная система обеспечения единства измерений. Метрология. Основные термины и определения
3 Определения и обозначения
3.1 В настоящих рекомендациях использованы следующие основные термины, определенные в Руководстве:
неопределенность (измерений): Параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые могли бы быть обоснованно приписаны измеряемой величине;
стандартная неопределенность (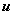 ): Неопределенность результата измерений, выраженная в виде среднего квадратического отклонения (СКО);
): Неопределенность результата измерений, выраженная в виде среднего квадратического отклонения (СКО);
суммарная стандартная неопределенность ( ): Стандартная неопределенность результата измерений, полученного через значения других величин, равная положительному квадратному корню суммы членов, причем члены являются дисперсиями или ковариациями этих других величин, взвешенными в соответствии с тем, как результат измерений изменяется при изменении этих величин;
): Стандартная неопределенность результата измерений, полученного через значения других величин, равная положительному квадратному корню суммы членов, причем члены являются дисперсиями или ковариациями этих других величин, взвешенными в соответствии с тем, как результат измерений изменяется при изменении этих величин;
расширенная неопределенность (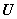 ): Величина, определяющая интервал вокруг результата измерений, в пределах которого, как можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могли бы быть приписаны измеряемой величине.
): Величина, определяющая интервал вокруг результата измерений, в пределах которого, как можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могли бы быть приписаны измеряемой величине.
3.2 В настоящих рекомендациях использованы следующие обозначения:
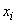 - оценка
- оценка 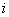 -й входной величины;
-й входной величины;
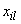 -
- 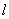 -й результат измерения
-й результат измерения 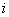 -й входной величины;
-й входной величины;
 - среднее арифметическое значение
- среднее арифметическое значение 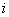 -й входной величины;
-й входной величины;
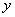 - оценка измеряемой величины;
- оценка измеряемой величины;
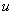 - стандартная неопределенность;
- стандартная неопределенность;
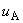 - стандартная неопределенность, оцененная по типу А;
- стандартная неопределенность, оцененная по типу А;
 - стандартная неопределенность, оцененная по типу В;
- стандартная неопределенность, оцененная по типу В;
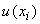 - стандартная неопределенность оценки
- стандартная неопределенность оценки 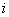 -й входной величины;
-й входной величины;
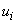 - стандартная неопределенность единичного измерения
- стандартная неопределенность единичного измерения 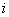 -й входной величины;
-й входной величины;
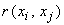 - коэффициент корреляции оценок
- коэффициент корреляции оценок 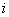 -й и
-й и 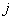 -й входных величин;
-й входных величин;
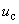 - суммарная стандартная неопределенность;
- суммарная стандартная неопределенность;
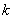 - коэффициент охвата;
- коэффициент охвата;
 - квантиль распределения Стъюдента для доверительной вероятности (уровня доверия)
- квантиль распределения Стъюдента для доверительной вероятности (уровня доверия) 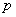 и числа степеней свободы
и числа степеней свободы 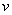 ;
;
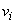 - число степеней свободы при вычислении неопределенности оценки
- число степеней свободы при вычислении неопределенности оценки 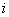 -й входной величины;
-й входной величины;
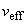 - эффективное число степеней свободы, принятое в Руководстве;
- эффективное число степеней свободы, принятое в Руководстве;
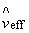 - оценка эффективного числа степеней свободы;
- оценка эффективного числа степеней свободы;
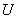 - расширенная неопределенность;
- расширенная неопределенность;
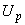 - расширенная неопределенность для уровня доверия
- расширенная неопределенность для уровня доверия 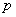 ;
;
 - СКО случайной погрешности результата измерений;
- СКО случайной погрешности результата измерений;
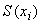 - СКО единичного измерения при многократных измерениях
- СКО единичного измерения при многократных измерениях 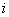 -й входной величины;
-й входной величины;
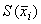 - СКО среднего арифметического значения при многократных измерениях
- СКО среднего арифметического значения при многократных измерениях 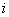 -й входной величины;
-й входной величины;
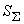 - СКО суммы случайных и неисключенных систематических погрешностей;
- СКО суммы случайных и неисключенных систематических погрешностей;
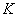 - коэффициент при суммировании систематической и случайной составляющих суммарной погрешности, принятый в НД ГСИ по метрологии*;
- коэффициент при суммировании систематической и случайной составляющих суммарной погрешности, принятый в НД ГСИ по метрологии*;
_______________
* Здесь и далее обобщенная ссылка "НД ГСИ по метрологии" означает группу нормативных документов по разделу 2 и нормативные документы по приложению Д - [2] и [3].
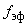 - оценка эффективного числа степеней свободы, принятая в НД ГСИ по метрологии;
- оценка эффективного числа степеней свободы, принятая в НД ГСИ по метрологии;
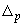 - доверительные границы суммарной погрешности результата измерений для доверительной вероятности
- доверительные границы суммарной погрешности результата измерений для доверительной вероятности 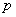 ;
;
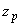 - квантиль нормального распределения для доверительной вероятности
- квантиль нормального распределения для доверительной вероятности 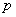 ;
;
 - границы
- границы 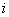 -й составляющей неисключенной систематической погрешности;
-й составляющей неисключенной систематической погрешности;
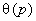 - доверительные границы систематической погрешности измерения для доверительной вероятности
- доверительные границы систематической погрешности измерения для доверительной вероятности 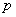 ;
;
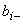 - нижняя граница отклонения измеряемой величины от результата измерений;
- нижняя граница отклонения измеряемой величины от результата измерений;
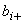 - верхняя граница отклонения измеряемой величины от результата измерений;
- верхняя граница отклонения измеряемой величины от результата измерений;
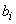 - симметричные границы отклонения измеряемой величины от результата измерений.
- симметричные границы отклонения измеряемой величины от результата измерений.
4 Рекомендации по применению Руководства
4.1 Основным количественным выражением неопределенности измерений является стандартная неопределенность 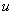 .
.
4.2 Основным количественным выражением неопределенности измерений, при котором результат определяют через значения других величин, является суммарная стандартная неопределенность 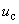 .
.
4.3 В тех случаях, когда это необходимо, вычисляют расширенную неопределенность 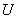 по формуле
по формуле
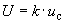 , (1)
, (1)
где 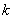 - коэффициент охвата (числовой коэффициент, используемый как множитель при суммарной стандартной неопределенности для получения расширенной неопределенности).
- коэффициент охвата (числовой коэффициент, используемый как множитель при суммарной стандартной неопределенности для получения расширенной неопределенности).
4.4 В Руководстве измеряемую величину 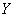 определяют как
определяют как
 , (2)
, (2)
где 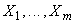 - входные величины (непосредственно измеряемые или другие величины, влияющие на результат измерения);
- входные величины (непосредственно измеряемые или другие величины, влияющие на результат измерения);
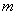 - число этих величин;
- число этих величин;
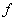 - вид функциональной зависимости.
- вид функциональной зависимости.
4.5 Оценку измеряемой величины 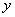 вычисляют как функцию оценок входных величин
вычисляют как функцию оценок входных величин 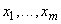 после внесения поправок на все известные источники неопределенности, имеющие систематический характер
после внесения поправок на все известные источники неопределенности, имеющие систематический характер
 . (3)
. (3)
4.6 Затем вычисляют стандартные неопределенности входных величин 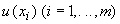 и возможные коэффициенты корреляции
и возможные коэффициенты корреляции  оценок
оценок 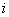 -й и
-й и 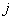 -й входных величин
-й входных величин 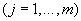 .
.
4.7 Различают два типа вычисления стандартной неопределенности:
вычисление по типу А - путем статистического анализа результатов многократных измерений;
вычисление по типу В - с использованием других способов.
4.8 Вычисление стандартной неопределенности 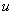
4.8.1 Вычисление стандартной неопределенности по типу А - 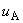
4.8.1.1 Исходными данными для вычисления 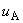 являются результаты многократных измерений:
являются результаты многократных измерений: 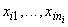 (где
(где 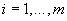 ;
; 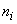 - число измерений
- число измерений 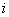 -й входной величины).
-й входной величины).
4.8.1.2 Стандартную неопределенность единичного измерения 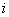 -й входной величины
-й входной величины 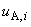 вычисляют по формуле
вычисляют по формуле
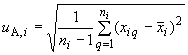 , (4)
, (4)
где 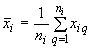 - среднее арифметическое результатов измерений
- среднее арифметическое результатов измерений 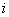 -й входной величины.
-й входной величины.
4.8.1.3 Стандартную неопределенность  измерений
измерений 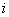 -й входной величины, при которых результат определяют как среднее арифметическое, вычисляют по формуле
-й входной величины, при которых результат определяют как среднее арифметическое, вычисляют по формуле
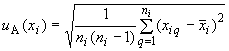 . (5)
. (5)
4.8.2 Вычисление стандартной неопределенности по типу В - 
4.8.2.1 В качестве исходных данных для вычисления  используют:
используют:
- данные предшествовавших измерений величин, входящих в уравнение измерения; сведения о виде распределения вероятностей;
- данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих приборов и материалов;
- неопределенности констант и справочных данных;
- данные поверки, калибровки, сведения изготовителя о приборе и т.п.
4.8.2.2 Неопределенности этих данных обычно представляют в виде границ отклонения значения величины от ее оценки. Наиболее распространенный способ формализации неполного знания о значении величины заключается в постулировании равномерного закона распределения возможных значений этой величины в указанных (нижней и верхней) границах [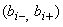 для
для 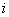 -й входной величины]. При этом стандартную неопределенность, вычисляемую по типу В -
-й входной величины]. При этом стандартную неопределенность, вычисляемую по типу В - 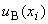 , определяют по формуле
, определяют по формуле
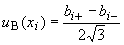 , (6)
, (6)
а для симметричных границ 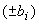 - по формуле
- по формуле
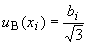 . (7)
. (7)
4.8.2.3 В случае других законов распределения формулы для вычисления неопределенности по типу В будут иными.
4.8.3 Для вычисления коэффициента корреляции 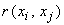 используют согласованные пары измерений
используют согласованные пары измерений 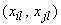 (где
(где 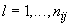 ;
; 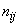 - число согласованных пар результатов измерений)
- число согласованных пар результатов измерений)
 . (8)
. (8)
4.9 Вычисление суммарной стандартной неопределенности 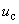
4.9.1 В случае некоррелированных оценок 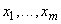 , суммарную стандартную неопределенность
, суммарную стандартную неопределенность 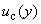 вычисляют по формуле
вычисляют по формуле
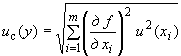 . (9)
. (9)
4.9.2 В случае коррелированных оценок 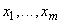 суммарную стандартную неопределенность вычисляют по формуле
суммарную стандартную неопределенность вычисляют по формуле
 , (10)
, (10)
где 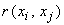 - коэффициент корреляции;
- коэффициент корреляции;
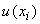 - стандартная неопределенность
- стандартная неопределенность 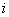 -й входной величины, вычисленная по типу А или В.
-й входной величины, вычисленная по типу А или В.
4.10 Выбор коэффициента охвата 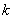 при вычислении расширенной неопределенности
при вычислении расширенной неопределенности
4.10.1 В общем случае коэффициент охвата 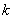 выбирают в соответствии с формулой
выбирают в соответствии с формулой
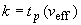 , (11)
, (11)
где 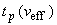 - квантиль распределения Стьюдента с эффективным числом степеней свободы
- квантиль распределения Стьюдента с эффективным числом степеней свободы 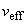 и доверительной вероятностью (уровнем доверия)
и доверительной вероятностью (уровнем доверия) 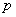 . Значения коэффициента
. Значения коэффициента 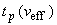 приведены в приложении Г.
приведены в приложении Г.
4.10.2 Эффективное число степеней свободы определяют по формуле
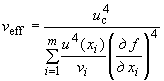 , (12)
, (12)
где 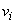 - число степеней свободы при определении оценки
- число степеней свободы при определении оценки 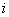 -й входной величины, при этом:
-й входной величины, при этом:
 - для вычисления неопределенностей по типу А;
- для вычисления неопределенностей по типу А;
 - для вычисления неопределенностей по типу В.
- для вычисления неопределенностей по типу В.
4.10.3 Во многих практических случаях при вычислении неопределенностей результатов измерений делают предположение о нормальности закона распределения возможных значений измеряемой величины и полагают:
 при
при 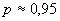 и
и 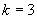 при
при 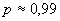 .
.
При предположении о равномерности закона распределения полагают:
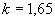 при
при 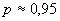 и
и 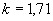 при
при 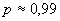 .
.
4.11 При представлении результатов измерений Руководство рекомендует приводить достаточное количество информации для возможности проанализировать или повторить весь процесс получения результата измерений и вычисления неопределенностей измерений, а именно:
- алгоритм получения результата измерений;
- алгоритм расчета всех поправок и их неопределенностей;
- неопределенности всех используемых данных и способы их получения;
- алгоритмы вычисления суммарной и расширенной неопределенностей (включая значение коэффициента 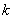 ).
).
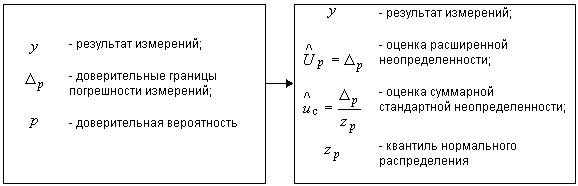
5 Соответствие между формами представления результатов измерений, используемыми в НД ГСИ по метрологии, и формой, используемой в Руководстве
5.1 При проведении совместных работ с зарубежными странами в работах, проводимых под эгидой МКМВ и его Консультативных комитетов, при подготовке публикаций в зарубежной печати, при публикациях работ по определению физических констант и в других случаях, связанных с выполнением международных метрологических работ, целесообразно руководствоваться нижеприведенными схемами.
5.1.1 При вычислении неопределенности измерений следует придерживаться последовательности, показанной на рисунке 1.
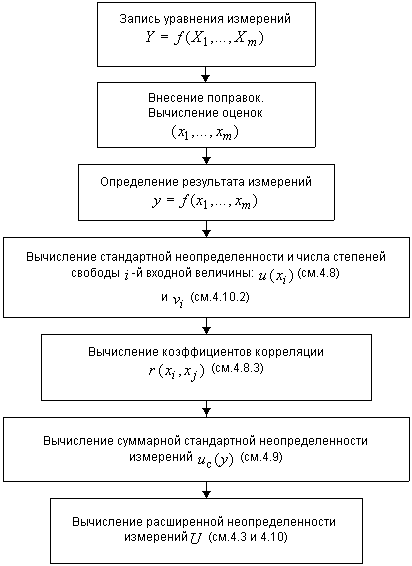
Рисунок 1
5.2 Сопоставление способов оценивания доверительных границ погрешности 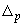 и вычисления расширенной неопределенности
и вычисления расширенной неопределенности 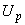 измерений приведено в таблице 1.
измерений приведено в таблице 1.
Таблица 1
|
|
|
| ||
|
НД ГСИ по метро- |
|
|
| |
|
где | ||||
|
и | ||||
|
| ||||
|
| ||||
|
Руко- |
где | |||
|
причем |
| |||
|
| ||||
|
Для большинства практических случаев в предположении: | ||||
|
- нормального закона распределения | ||||
|
- равномерного закона распределения | ||||
5.3 При сопоставлении оценок характеристик погрешности и неопределенностей результатов измерений рекомендуется использовать следующую схему (с учетом пояснений А.5 и А.6 приложения А):
|
СКО, характеризующее случайную погрешность |
|
Стандартная неопределенность, вычисленная по типу А |
|
СКО, характеризующее неисключенную систематическую погрешность |
|
Стандартная неопределенность, вычисленная по типу В |
|
СКО, характеризующее суммарную погрешность |
|
Суммарная стандартная неопределенность |
|
Доверительные границы погрешности |
|
Расширенная неопределенность |
5.4 Если отсутствует достаточная информация для вычисления неопределенности 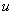 в соответствии с Руководством (раздел 4 настоящей рекомендации), то ее оценка
в соответствии с Руководством (раздел 4 настоящей рекомендации), то ее оценка 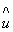 может быть получена на основании оценок характеристик погрешности по приведенным ниже схемам. Схемы 1 и 2 соответствуют двум различным способам представления результатов измерений, принятым в НД ГСИ по метрологии. Необходимо отметить, что оценки неопределенностей, полученные таким образом, в ряде случаев не совпадают со значениями неопределенностей, полученными в соответствии с Руководством (см. приложение В).
может быть получена на основании оценок характеристик погрешности по приведенным ниже схемам. Схемы 1 и 2 соответствуют двум различным способам представления результатов измерений, принятым в НД ГСИ по метрологии. Необходимо отметить, что оценки неопределенностей, полученные таким образом, в ряде случаев не совпадают со значениями неопределенностей, полученными в соответствии с Руководством (см. приложение В).
Схема 1

Схема 2
Оценить неопределенности 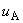 и
и  по отдельности, зная только
по отдельности, зная только 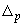 , невозможно.
, невозможно.
ПРИЛОЖЕНИЕ А
(справочное)
Сравнительный анализ двух подходов к выражению характеристик точности измерений
A.1 Целью измерений является получение оценки истинного значения измеряемой величины. Понятие погрешности измерений как разности между результатом измерений и истинным (действительным) значением измеряемой величины используется для описания точности измерений в НД ГСИ по метрологии. Говоря об оценивании погрешности, в метрологической практике государств - участников Соглашения подразумевают оценивание ее характеристик.

А.2 В Руководстве для выражения точности измерений вводят понятие неопределенности измерений. Неопределенность измерений понимают как неполное знание значения измеряемой величины и для количественного выражения этой неполноты вводят распределение вероятностей возможных (обоснованно приписанных) значений измеряемой величины. Таким образом, параметр этого распределения (также называемый - неопределенность) количественно характеризует точность результата измерений.
А.3 Сходными для обоих подходов являются последовательности действий при оценивании характеристик погрешности и вычислении неопределенности измерений:
- анализ уравнения измерений;
- выявление всех источников погрешности (неопределенности) измерений и их количественное оценивание;
- введение поправок на систематические погрешности (эффекты), которые можно исключить.
А.4 Методы вычисления неопределенности, так же как и методы оценивания характеристик погрешности, заимствованы из математической статистики, однако при этом используются различные интерпретации закона распределения вероятностей случайных величин. Кроме изложенных в Руководстве и НД ГСИ по метрологии методов вычисления неопределенности и оценивания характеристик погрешности на практике используют и другие методы.
Возможные различия между оценками характеристик погрешности (в соответствии с НД ГСИ по метрологии) и неопределенностями (в соответствии с Руководством) показаны в примерах, приведенных в приложениях Б и В.
Различие двух подходов проявляется также в трактовке неопределенности и характеристик погрешности, основанной на разных интерпретациях вероятности: частотной и субъективной. В частности, доверительные границы погрешности (откладываемые от результата измерений) накрывают истинное значение измеряемой величины с заданной доверительной вероятностью (частотная интерпретация вероятности). В то же время аналогичный интервал 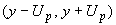 трактуется в Руководстве как интервал, содержащий заданную долю распределения значений, которые могли бы быть обоснованно приписаны измеряемой величине (субъективная интерпретация вероятности).
трактуется в Руководстве как интервал, содержащий заданную долю распределения значений, которые могли бы быть обоснованно приписаны измеряемой величине (субъективная интерпретация вероятности).
А.5 В общем случае не существует однозначного соответствия между случайными погрешностями и неопределенностями, вычисленными по типу А (а также неисключенными систематическими погрешностями и неопределенностями, вычисленными по типу В). Деление на систематические и случайные погрешности обусловлено природой их возникновения и проявления в ходе измерительного эксперимента, а деление на неопределенности, вычисляемые по типу А и по типу В, - методами их расчета.
А.6 Результаты сравнительного анализа процедур оценивания характеристик погрешности и вычисления неопределенности измерений приведены в таблицах A.1 и А.2.
Таблица A.1 - Процедура оценивания характеристик погрешности результата измерений
|
Погрешность |
| |||
|
Модель погрешности |
| |||
|
Характеристики погрешности |
|
|
| |
|
Исходные данные для оценивания характеристик погрешности |
1 Модель объекта исследования. | |||
|
2 Экспериментальные данные | ||||
|
3 Информация о законах распределения. | ||||
|
4 Сведения об источниках погрешностей, их природе и характеристиках составляющих | ||||
|
5 Стандартные справочные данные и другие справочные материалы | ||||
|
Методы оценивания характеристик: |
| |||
|
1 случайных погрешностей |
| |||
|
| ||||
|
2 неисключенных систематических погрешностей |
| |||
|
|
где | |||
|
3 суммарной погрешности |
| |||
|
Форма представления характеристик погрешности |
|
| ||
|
Интерпретация полученных результатов |
Интервал | |||
Таблица А.2 - Процедура вычисления неопределенности измерений
|
Модель неопределенности (представление знания о значении измеряемой величины) |
| ||
|
Неопределенность (количественная мера) |
Стандартная |
Суммарная |
Расширенная |
|
Исходные данные для вычисления неопределенности |
1 Модель объекта исследования. | ||
|
2 Экспериментальные данные | |||
|
3 Информация о законах распределения. | |||
|
4 Сведения об источниках неопределенности и информация о значениях неопределенности. | |||
|
5 Стандартные справочные данные и другие справочные материалы | |||
|
Методы вычисления неопределенности: |
| ||
|
1 по типу А |
| ||
|
2 по типу В |
| ||
|
3 расширенной неопределенности |
| ||
|
где | |||
|
|
| ||
|
| |||
|
Представление неопределенности |
| ||
|
Интерпретация полученных результатов |
Интервал | ||
ПРИЛОЖЕНИЕ Б
(справочное)
Пример оценивания характеристик погрешности и вычисления неопределенности измерений. Измерения силы электрического тока с помощью вольтметра и токового шунта
Б.1 Уравнение измерений
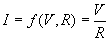 , (Б.1)
, (Б.1)
где 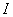 - сила тока;
- сила тока;
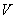 - напряжение;
- напряжение;
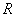 - сопротивление шунта.
- сопротивление шунта.
Б.2 Нахождение результата измерений
Б.2.1 В результате измерений напряжения при температуре  °С получают ряд значений
°С получают ряд значений 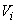 в милливольтах (где
в милливольтах (где 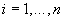 ;
; 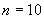 ):
):
100,68; 100,83; 100,79; 100,64; 100,63; 100,94; 100,60; 100,68; 100,76; 100,65.
Б.2.2 На основе полученных значений вычисляют среднее арифметическое значение напряжения 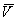 , мВ, по формуле
, мВ, по формуле
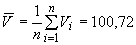 . (Б.2)
. (Б.2)
Б.2.3 Значение сопротивления шунта 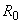 , Ом, установлено при его калибровке для
, Ом, установлено при его калибровке для  А и
А и 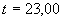 °С и равно:
°С и равно:
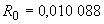 .
.
Б.2.4 Результат измерений силы тока 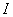 , А, получают по формуле
, А, получают по формуле
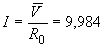 . (Б.3)
. (Б.3)
Б.3 Анализ источников погрешности результата измерений
Б.3.1 СКО, характеризующее случайную составляющую погрешности при измерениях напряжения 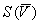 , мВ, вычисляют по формуле
, мВ, вычисляют по формуле
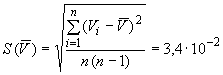 , (Б.4)
, (Б.4)
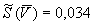 %*.
%*.
_______________
* Здесь и далее знак тильды над буквой, обозначающей характеристику погрешности (неопределенности), означает, что данная характеристика приведена в относительном виде.
Б.3.2 Границы неисключенной систематической погрешности вольтметра в милливольтах определены при его калибровке в виде следующего выражения*:
_______________
* В выражениях для границ погрешностей при равных значениях отклонений от нуля знак ± здесь и далее опущен.
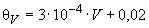 . (Б.5)
. (Б.5)
Тогда при 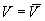 получают
получают
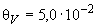 мB,
мB,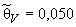 %.
%.
Б.3.3 Границы неисключенной систематической погрешности значения сопротивления шунта, определенные при его калибровке, равны
 %.
%.
Тогда при 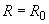 получают
получают
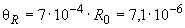 Ом. (Б.6)
Ом. (Б.6)
Б.3.4 Границы неисключенной систематической составляющей погрешности значения сопротивления шунта, обусловленной погрешностью измерений температуры, находят из формулы, определяющей зависимость сопротивления от температуры
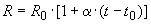 , (Б.7)
, (Б.7)
где 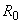 - значение сопротивления при
- значение сопротивления при 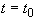 (
( 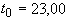 °С;
°С; 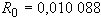 Ом);
Ом);
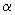 - температурный коэффициент
- температурный коэффициент 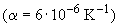 .
.
В случае, когда границы погрешности измерения температуры равны 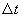 , границы соответствующей составляющей погрешности значения сопротивления равны
, границы соответствующей составляющей погрешности значения сопротивления равны
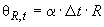 , (Б.8)
, (Б.8)
Таким образом, при 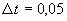 °С получают:
°С получают:
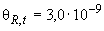 Ом,
Ом,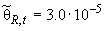 %.
%.
В дальнейшем эту составляющую погрешности (ввиду ее малости по сравнению с другими составляющими) можно не учитывать.
Б.4 Вычисление характеристик погрешности результата измерений
Б.4.1 Делают предположение о равномерном распределении неисключенных систематических составляющих погрешности результата измерений внутри их границ  и
и  . Тогда СКО суммарной неисключенной систематической составляющей погрешности результата измерений силы тока
. Тогда СКО суммарной неисключенной систематической составляющей погрешности результата измерений силы тока 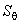 , А, определяют по формуле
, А, определяют по формуле
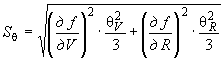 , (Б.9)
, (Б.9)
где 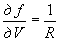 ,
, 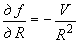 - коэффициенты влияния.
- коэффициенты влияния.
Таким образом, получают
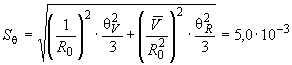 А,
А,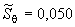 %.
%.
Б.4.2 Доверительные границы суммарной неисключенной систематической составляющей погрешности результата измерений силы тока 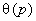 при доверительной вероятности
при доверительной вероятности 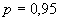 оценивают по формуле
оценивают по формуле
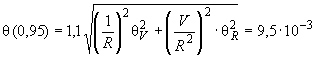 А, (Б.10)
А, (Б.10)
 %.
%.
Б.4.3 СКО случайной составляющей погрешности результата измерений силы тока  определяют по формуле
определяют по формуле
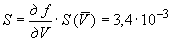 А, (Б.11)
А, (Б.11)
 %.
%.
Б.4.4 СКО суммарной погрешности результата измерений силы тока 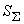 вычисляют по формуле
вычисляют по формуле
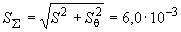 А, (Б.12)
А, (Б.12)
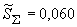 %.
%.
Б.4.5 Доверительные границы погрешности результата измерений силы тока 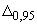 при
при 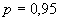 и эффективном числе степеней свободы
и эффективном числе степеней свободы 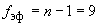 вычисляют по формуле
вычисляют по формуле
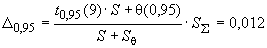 A, (Б.13)
A, (Б.13)
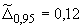 %.
%.
Б.5 Вычисление неопределенности измерений
Б.5.1 По типу А вычисляют стандартную неопределенность, обусловленную источниками неопределенности, имеющими случайный характер.
Б.5.1.1 Стандартную неопределенность напряжения, обусловленную источниками неопределенности, имеющими случайный характер, 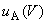 определяют по формуле
определяют по формуле
 , (Б.14)
, (Б.14)
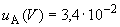 мВ,
мВ, 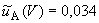 %.
%.
Б.5.1.2 Стандартную неопределенность силы тока, обусловленную источниками неопределенности, имеющими случайный характер, 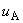 определяют по формуле
определяют по формуле
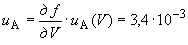 А, (Б.15)
А, (Б.15)
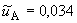 %.
%.
Б.5.2 По типу В вычисляют стандартные неопределенности, обусловленные источниками неопределенности, имеющими систематический характер. Распределение значений величин внутри границ считают равномерным.
Б.5.2.1 Границы систематического смещения при измерениях напряжения, определенные при калибровке вольтметра, равны 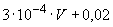 . Тогда соответствующую стандартную неопределенность
. Тогда соответствующую стандартную неопределенность 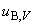 вычисляют по формуле
вычисляют по формуле
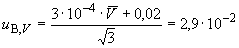 мВ, (Б.16)
мВ, (Б.16)
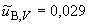 %.
%.
Б.5.2.2 Границы, внутри которых лежит значение сопротивления шунта, определены при калибровке шунта и равны 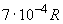 . Тогда при
. Тогда при 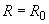 соответствующую стандартную неопределенность
соответствующую стандартную неопределенность  вычисляют по формуле
вычисляют по формуле
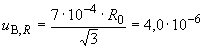 Ом, (Б.17)
Ом, (Б.17)
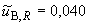 %.
%.
Б.5.2.3 Границы изменения значения сопротивления шунта, обусловленного изменением температуры, равны 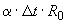 . Соответствующую стандартную неопределенность
. Соответствующую стандартную неопределенность 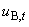 получают в соответствии с формулой
получают в соответствии с формулой
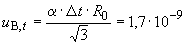 Ом, (Б.18)
Ом, (Б.18)
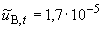 %.
%.
В дальнейшем этой составляющей неопределенности (ввиду ее малости по сравнению с другими составляющими) можно пренебречь.
Б.5.2.4 Суммарную стандартную неопределенность  , вычисленную по типу В, определяют по формуле
, вычисленную по типу В, определяют по формуле
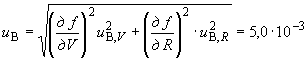 A, (Б.19)
A, (Б.19)
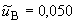 %.
%.
Б.5.3 Суммарную стандартную неопределенность 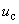 вычисляют по формуле
вычисляют по формуле
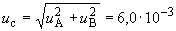 А, (Б.20)
А, (Б.20)
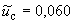 %.
%.
Б.5.4 Эффективное число степеней свободы 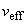 рассчитывают по формуле
рассчитывают по формуле
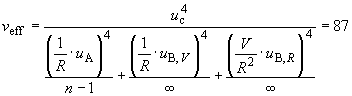 . (Б.21)
. (Б.21)
Б.5.5 Коэффициент охвата 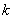 получают по формуле
получают по формуле
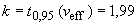 . (Б.22)
. (Б.22)
Б.5.6 Расширенную неопределенность 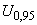 определяют следующим образом
определяют следующим образом
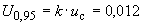 А, (Б.23)
А, (Б.23)
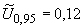 %.
%.
Б.6 Переход от характеристик погрешности к неопределенности измерений
Б.6.1 Используя оценки характеристик погрешности, полученные в Б.3 и Б.4 настоящего приложения, можно продемонстрировать получение оценок неопределенностей в соответствии с 5.4 настоящих рекомендаций.
В данном примере неопределенности измерений, вычисленные в Б.5 настоящего приложения в соответствии с Руководством, совпадают с их оценками, полученными по схеме 1.
Схема 1
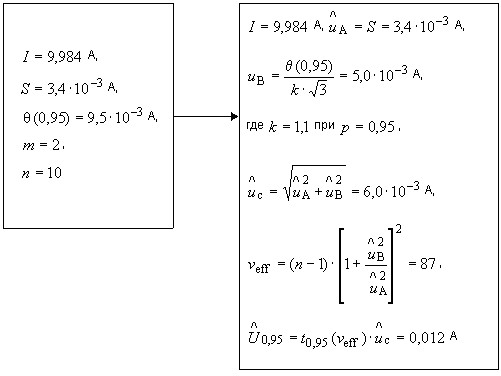
В данном примере разность неопределенностей измерений, вычисленных в Б.5 настоящего приложения в соответствии с Руководством, и их оценок, полученных по схеме 2, меньше погрешности округления при вычислениях.
Схема 2

ПРИЛОЖЕНИЕ В
(справочное)
Пример оценивания характеристик погрешности и вычисления неопределенности измерений. Измерения длины штриховой меры
Измерение длины штриховой меры проводят на государственном первичном эталоне единицы длины интерференционным методом.
B.1 Уравнение измерений
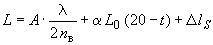 , (B.1)
, (B.1)
где 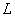 - длина штриховой меры;
- длина штриховой меры;
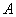 - число импульсов;
- число импульсов;
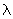 - длина волны излучения (
- длина волны излучения (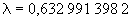 мкм);
мкм);
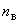 - показатель преломления воздуха (
- показатель преломления воздуха (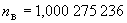 );
);
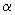 - коэффициент линейного расширения (
- коэффициент линейного расширения (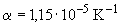 );
);
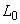 - опорное значение длины штриховой меры (
- опорное значение длины штриховой меры ( м);
м);
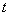 - температура штриховой меры (
- температура штриховой меры (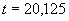 °С);
°С);
 - поправка на размер коллиматорной щели (
- поправка на размер коллиматорной щели ( мкм).
мкм).
В.2 Нахождение результата измерений
В.2.1 В результате измерений числа импульсов и внесения поправок на известные систематические погрешности в соответствии с уравнением измерения (B.1) получают ряд значений длины штриховой меры 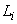 в метрах (где
в метрах (где  ;
; 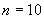 ):
):
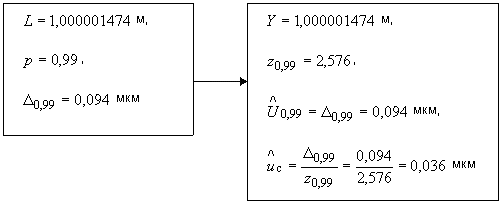
1,000 001 356; 1,000 001 584; 1,000 001 383; 1,000 001 469; 1,000 001 491; 1,000 001 466; 1,000 001 575; 1,000 001 397; 1,000 001 405; 1,000 001 334.
В.2.2 Оценку значения длины штриховой меры 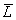 как среднее арифметическое значений
как среднее арифметическое значений 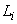 определяют по формуле
определяют по формуле
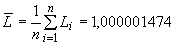 . (В.2)
. (В.2)
В.3 Анализ источников погрешности результата измерений
В.3.1 СКО случайной составляющей погрешности  , м, определяют по формуле*
, м, определяют по формуле*
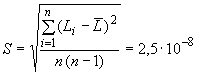 , (В.3)
, (В.3)
 мкм.
мкм.
_______________
* Для более компактной записи значения характеристик погрешности (неопределенности) далее будут выражены в микрометрах (мкм).
В.3.2 Границы неисключенных систематических погрешностей:
- определения показателя преломления воздуха 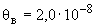 ;
;
- значения длины волны  мкм;
мкм;
- определения температуры меры  °С;
°С;
- определения поправки на размер коллиматорной щели 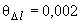 мкм.
мкм.
Составляющие погрешности результата измерений, обусловленные погрешностями значений 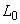 и
и 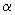 , пренебрежимо малы.
, пренебрежимо малы.
В.4 Вычисление характеристик погрешности результата измерений
В.4.1 В предположении о равномерном распределении неисключенных систематических составляющих суммарной погрешности внутри границ  ,
, 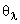 ,
, 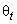 и
и  СКО неисключенной систематической составляющей погрешности результата измерений
СКО неисключенной систематической составляющей погрешности результата измерений 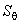 вычисляют по формуле
вычисляют по формуле
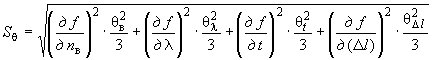 , (В.4)
, (В.4)
где - 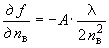 ;
; 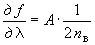 ;
; 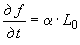 ;
; 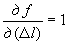 - коэффициенты влияния.
- коэффициенты влияния.
Таким образом, получают:
 . (В.5)
. (В.5)
Для упрощения расчетов можно принять:  м,
м, 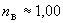 ,
, 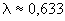 мкм.
мкм.
Тогда получают:
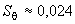 мкм.
мкм.
В.4.2 Доверительные границы неисключенной систематической погрешности результата измерений при 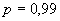 и числе неисключенных составляющих систематической погрешности
и числе неисключенных составляющих систематической погрешности 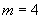 (
(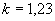 по [3]) -
по [3]) - 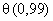 вычисляют по формуле
вычисляют по формуле
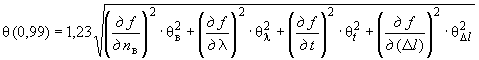 . (B.6)
. (B.6)
Рассчитывая коэффициенты влияния по В.4.1, получают
 мкм.
мкм.
В.4.3 СКО суммарной погрешности 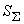 , мкм, определяют по формуле
, мкм, определяют по формуле
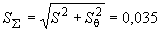 . (В.7)
. (В.7)
В.4.4 Доверительные границы суммарной погрешности  при
при 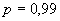 и
и 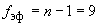 вычисляют по формуле
вычисляют по формуле
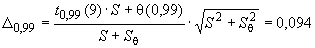 мкм. (В.8)
мкм. (В.8)
В.5 Вычисление неопределенности измерений
В.5.1 По типу А вычисляют стандартную неопределенность 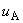 , обусловленную источниками неопределенности, имеющими случайный характер при измерении длины штриховой меры, по формуле
, обусловленную источниками неопределенности, имеющими случайный характер при измерении длины штриховой меры, по формуле
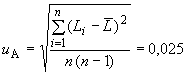 мкм. (В.9)
мкм. (В.9)
В.5.2 По типу В вычисляют стандартные неопределенности, обусловленные источниками неопределенности, имеющими систематический характер. Закон распределения величин внутри границ считают равномерным.
В.5.2.1 Границы, внутри которых лежит значение показателя преломления воздуха, равны 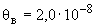 . Стандартную неопределенность, обусловленную неточным знанием данного параметра,
. Стандартную неопределенность, обусловленную неточным знанием данного параметра, 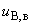 определяют как
определяют как
 . (В.10)
. (В.10)
В.5.2.2 Границы, внутри которых лежит значение длины волны излучения, равны  мкм. Тогда соответствующую стандартную неопределенность
мкм. Тогда соответствующую стандартную неопределенность 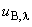 вычисляют по формуле
вычисляют по формуле
 мкм. (В.11)
мкм. (В.11)
В.5.2.3 Границы, внутри которых лежит значение температуры штриховой меры, равны  °С. Стандартную неопределенность, обусловленную неточным знанием температуры,
°С. Стандартную неопределенность, обусловленную неточным знанием температуры, 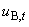 вычисляют по формуле
вычисляют по формуле
 °C. (В.12)
°C. (В.12)
В.5.2.4 Границы, внутри которых лежит значение поправки на размер коллиматорной щели, равны 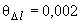 мкм. Тогда соответствующую стандартную неопределенность
мкм. Тогда соответствующую стандартную неопределенность 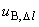 получают по формуле
получают по формуле
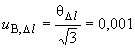 мкм. (В.13)
мкм. (В.13)
В.5.2.5 Суммарную стандартную неопределенность, вычисленную по типу В, -  определяют по формуле
определяют по формуле
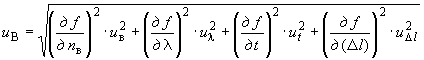 . (В.14)
. (В.14)
Расчет коэффициентов влияния - по В.4.1:
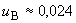 мкм.
мкм.
В.5.3 Суммарную стандартную неопределенность 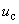 вычисляют по формуле
вычисляют по формуле
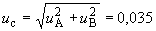 мкм. (В.15)
мкм. (В.15)
В.5.4 Эффективное число степеней свободы 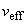 определяют по формуле
определяют по формуле
 . (В.16)
. (В.16)
В. 5.5 Коэффициент охвата 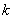 определяют следующим образом
определяют следующим образом
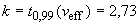 . (В.17)
. (В.17)
В.5.6 Расширенную неопределенность 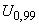 определяют как
определяют как
 мкм. (В.18)
мкм. (В.18)
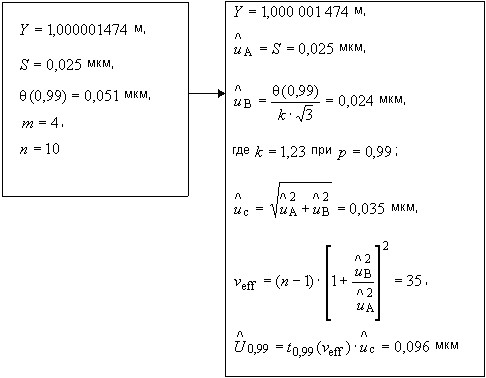
В.6 Переход от характеристик погрешности к неопределенности измерений
В.6.1 Используя оценки характеристик погрешности, полученные в В.4 настоящего приложения, можно продемонстрировать получение оценок неопределенностей в соответствии с 5.4 настоящих рекомендаций.
В данном примере неопределенности измерений, вычисленные по В.5 настоящего приложения в соответствии с Руководством, совпадают с их оценками, полученными по схеме 1.
Схема 1
Относительные разности неопределенностей измерений, вычисленных по В.5 настоящего приложения в соответствии с Руководством, и их оценок, полученных по схеме 2 (когда отсутствует достаточная информация для их оценки в соответствии с Руководством), в данном примере равны:
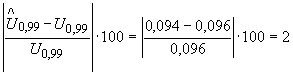 %,
%,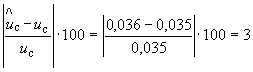 %.
%.
Схема 2
ПРИЛОЖЕНИЕ Г
(справочное)
Значения коэффициента  для случайной величины, имеющей
для случайной величины, имеющей
распределение Стьюдента с 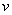 степенями свободы
степенями свободы
|
|
| |
|
|
| |
|
3 |
3,182 |
5,841 |
|
4 |
2,776 |
4,604 |
|
5 |
2,571 |
4,032 |
|
6 |
2,447 |
3,707 |
|
7 |
2,365 |
3,499 |
|
8 |
2,306 |
3,355 |
|
9 |
2,262 |
3,250 |
|
10 |
2,228 |
3,169 |
|
12 |
2,179 |
3,055 |
|
14 |
2,145 |
2,977 |
|
16 |
2,120 |
2,921 |
|
18 |
2,101 |
2,878 |
|
20 |
2,086 |
2,845 |
|
22 |
2,074 |
2,819 |
|
24 |
2,064 |
2,797 |
|
26 |
2,056 |
2,779 |
|
28 |
2,048 |
2,763 |
|
30 |
2,042 |
2,750 |
|
|
1,960 |
2,576 |
ПРИЛОЖЕНИЕ Д
(справочное)
Библиография
[1] Руководство по выражению неопределенности измерения. Перевод с английского под редакцией В.А.Слаева. - ВНИИМ. - С-Пб, 1999*
_______________
* Подлинник документа - Guide to the Expression of Uncertainty in Measurement: First edition. - ISO, Switzerland, 1993 находится во ВНИИКИ Госстандарта России.
[2] МИ 1317-86 Государственная система обеспечения единства измерений. Результаты и характеристики погрешности измерений. Формы и способы представления. Способы использования при испытаниях образцов продукции и контроле их параметров
[3] МИ 2083-90 Государственная система обеспечения единства измерений. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей
Текст документа сверен по:
официальное издание
М.: ИПК Издательство стандартов, 2003

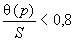
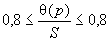
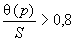
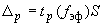 ,
,  ,
,
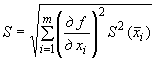 ;
; 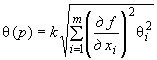 , здесь
, здесь 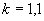 при
при  при
при 
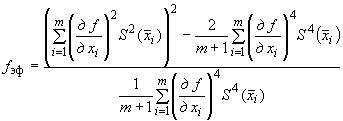
 ,
,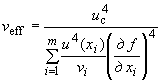 ,
,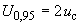 ,
,  ;
;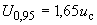 ,
, 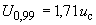

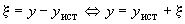
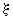 - случайная величина с плотностью распределения вероятностей
- случайная величина с плотностью распределения вероятностей 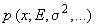 , где
, где 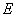 - математическое ожидание,
- математическое ожидание, 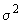 - дисперсия
- дисперсия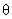 - границы неисключенной систематической погрешности
- границы неисключенной систематической погрешности 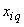 , где
, где  ;
; 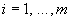 .
. 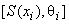 , структурная модель погрешности.
, структурная модель погрешности. 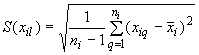 ;
; 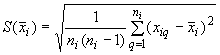 ;
; ,
,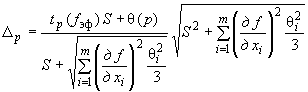
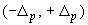 с вероятностью
с вероятностью  с вероятностью
с вероятностью 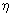 - случайная величина с плотностью распределения вероятностей
- случайная величина с плотностью распределения вероятностей 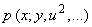 , где
, где 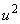 - дисперсия
- дисперсия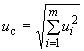
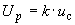
 , где
, где  ;
; 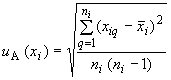
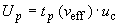 ,
,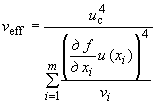 ;
; 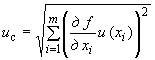 ;
;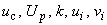
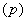 распределения значений, которые могли бы быть обоснованно приписаны измеряемой величине.
распределения значений, которые могли бы быть обоснованно приписаны измеряемой величине.
 «Сводничество – уголовно наказуемое дело!» Роза Сябитова...
«Сводничество – уголовно наказуемое дело!» Роза Сябитова...  Создайте свой интернет-магазин на новой платформе ReadyScript
Создайте свой интернет-магазин на новой платформе ReadyScript  Хостинг, домены, VPS/VDS, размещение серверов
Хостинг, домены, VPS/VDS, размещение серверов